三相变流器矢量控制及参数设计系列(2):PWM原理
这是关于矢量控制的系列文章,上一篇文章简单介绍了矢量控制策略的基本思想和框架,本文主要介绍矢量控制策略中脉冲宽度调制(PWM)的相关内容。
可移步【同名WX:MlabWhispers电气】
往期内容:
三相变流器矢量控制及参数设计系列(1):引言
1 理论分析
1.1 基础知识
脉冲宽度调制(Pulse Width Modulation,PWM)是一种通过比较调制波和载波调节开关信号脉冲宽度以控制开关管导通的技术,在调制信号为正弦信号时被称为正弦脉冲宽度调制,即SPWM。载波信号一般为三角信号。
根据载波信号的差异,有三种常见的SPWM,分别是:
双极性SPWM——三角波有正负双极性,桥臂输出电压也有正负双极性。
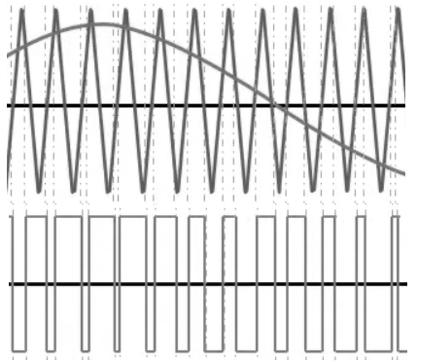
单极性SPWM——三角波只有正零或负零单极性,桥臂输出电压宜是如此。
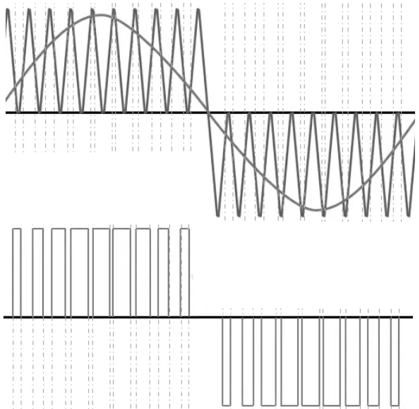
单极倍频SPWM——调制波及其反向波与三角波比较共同产生开关信号。这样可以使桥臂内电势谐波频率集中在两倍开关频率处,从而可以将滤波器转折频率设计得更大,滤波器体积设计得更小。
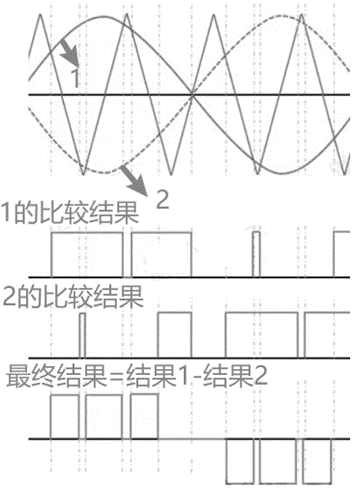
对于三相桥式拓扑,使用SPWM时桥臂相电压最大幅值为Udc/2,即直流电源利用率=Udc/2*sqrt(3)/Udc=sqrt(3)/2,相对较低。由此,在SPWM的基础上,对正弦调制波做一定处理就产生了另外两种常见的PWM,分别是:
三次谐波注入SPWM——在正弦调制波中叠加特定比例的三次谐波,形成“马鞍形”调制波,再与三角载波比较。直流电压利用率可达1,三次谐波在线电压中抵消。(具体可参考ZhiHu文章三次谐波注入法)
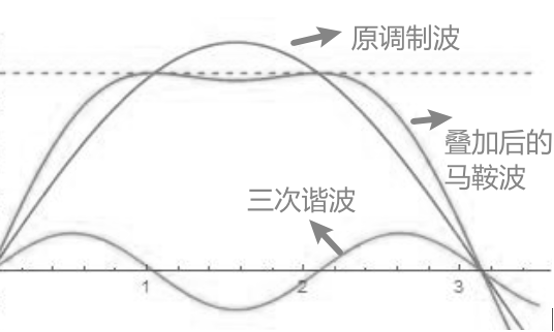
SVPWM——将三相正弦调制波映射为αβ坐标系下的空间矢量,通过构建出一系列可实现的矢量,在每个控制周期内选择合适的矢量及其作用时间来逼近正弦调制波的空间矢量。直流电压利用率可达1,谐波含量低,分布分散。(具体可参考ZhiHu文章彻底吃透SVPWM如此简单,讲解的非常详细透彻!)
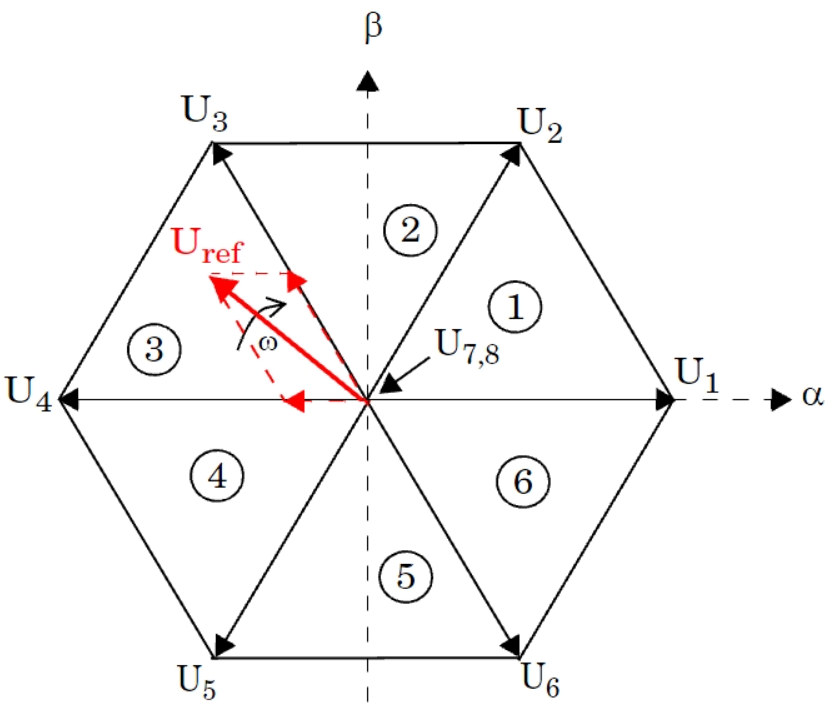
本文以最基础的双极性SPWM为例进行说明。
1.2 基于PWM的三相变流系统
基于PWM的三相变流系统示意图如下:
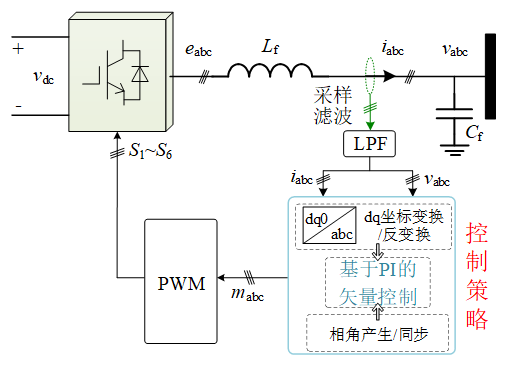
图中,Lf,Cf为滤波电感和滤波电容;vdc为直流侧电压;eabc为三相变流器输出的内电势基波分量;iabc为电感电流;vabc为电容电压;Q1~Q6为开关管的PWM信号。其中,三相全桥变流器的拓扑如下所示:
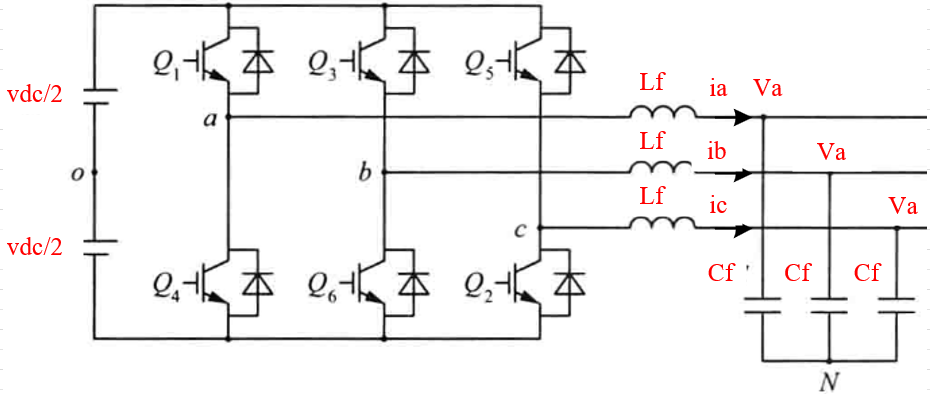
上图可等效为如下电路:
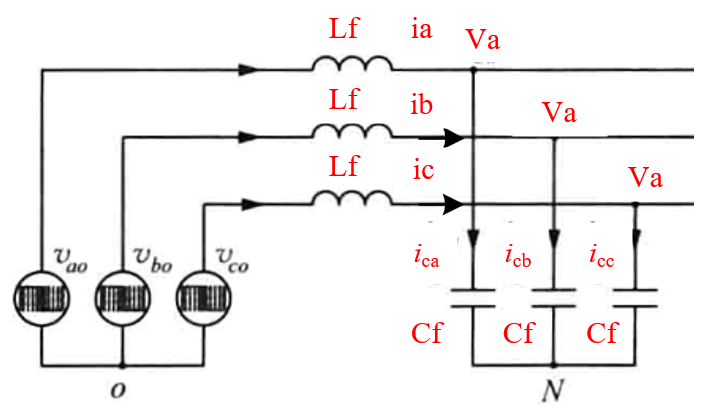
图中,vao,vbo和vco分别为abc桥臂中点a,b,c相对于直流电压中点o的电压,由直流电压值和开关状态共同决定,如vao在开关1导通时为vdc/2,在开关4导通时为-vdc/2。另外,开关状态由PWM产生的开关信号决定,而开关信号又由调制波和载波共同决定。调制波由闭环控制生成,为目标正弦基波信号,包含了幅值VM,频率f1,初相角等关键信息;载波一般为三角波,包含幅值Vtri,频率fsw等关键信息。根据傅里叶变换,vao,vbo和vco由基波频率的正弦波,三角波频率的正弦波及二者频率组合的正弦波叠加而成。
根据上述等效电路图,易得
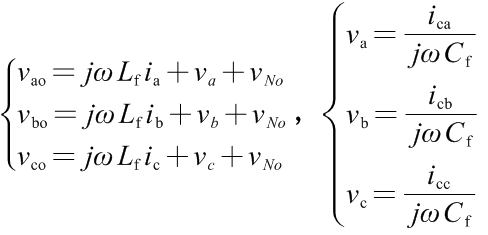
对于三相三线接法,零序通路不存在,零序电流为0,即ia+ib+ic=0,ica+icb+icc=0。那么,
![]()
由于vao,vbo和vco三相不平衡(因为含有谐波),因此零序电压VNo≠0,即N点和o点的电位不同。那么,
![]()
由上式可知,vaN也会包含基波分量以及载波频率附近的谐波分量,不妨设
![]()
其中,ea为基波分量;eah为各个谐波分量,主要集中在开关频率附近。b,c相同理,不再赘述。那么,等效电路可进一步等效为
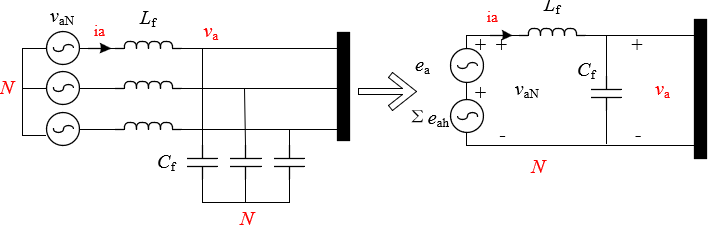
根据叠加定理,上述电路可视为ea和Σeah单独作用时效果的叠加,如下图:
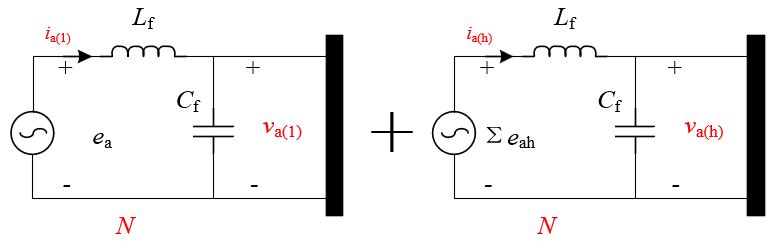
然而,LC低通滤波电路存在的目的就是滤除高频开关谐波,其转折频率fc=1/sqrt(LfCf)一般设置为开关频率的1/10以下,基波频率的10倍以上,从而在基本不影响基波分量的前提下有效滤波高频谐波分量。因此,Σeah经LC滤波器后的作用十分微小,可以忽略,即主电路可进一步简化为:
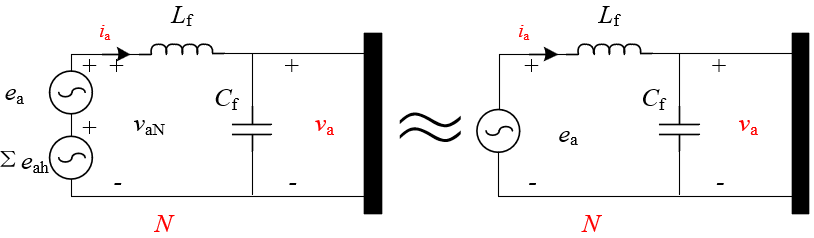
这样一来,只需关注内电势的基波分量eabc即可。设三相调制波mabc的表达式为:
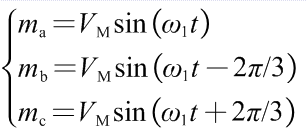
其中,VM为调制波幅值;w1为基波角频率。
在三相全桥拓扑及PWM下,ea与调制波ma的关系满足:
![]()
其中,Mr为调制比,定义为:
![]()
在调制过程中,对于SPWM,要求VM≤Vtri,即Mr≤1;对于三次谐波注入SPWM或SVPWM,Mr≤2/sqrt(3)。在SPWM下,三相全桥拓扑能够输出的内电势基波分量最大幅值为vdc/2。此时,如果在控制环路中对调制波以vdc/2为基准进行归一化,并将Vtri设置为1,那么
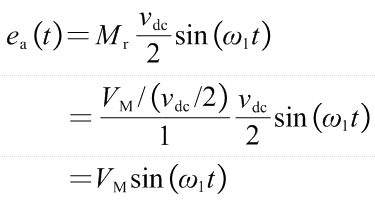
内电势基波分量将与归一化前的调制波完成保持一致。但需要注意,由于Mr=Vm/(vdc/2)/1≤1,VM不能超过最大幅值vdc/2。
注:详细推导过程及表达式请参见书籍《阮新波. LCL型并网逆变器的控制技术_阮新波[M]. 科学出版社, 2015,p21-p33.》。这里给出其中的一些关键表达式供大家参考:
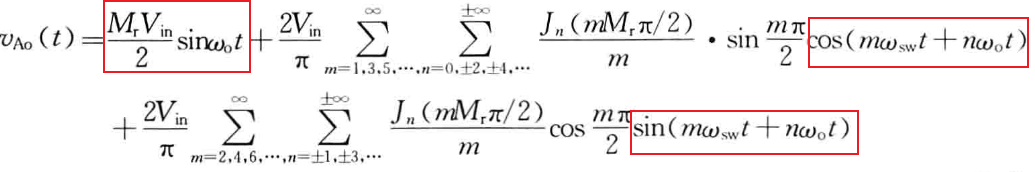
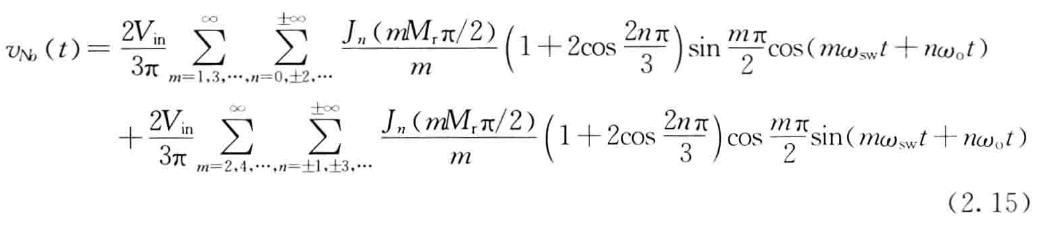
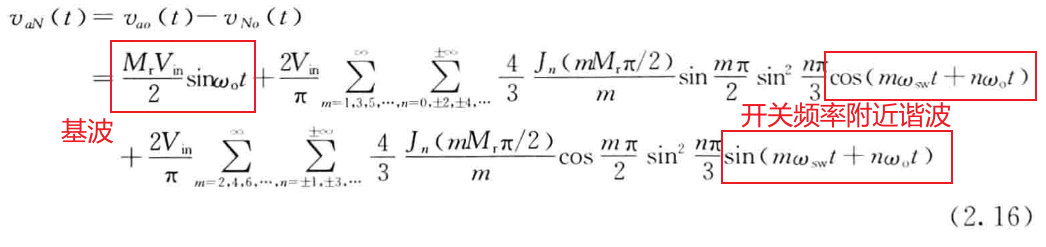
2 仿真验证
2.1 仿真模型
为了验证上述理论分析,通过MATLAB/Simulink平台搭建了相应仿真,如下图所示:
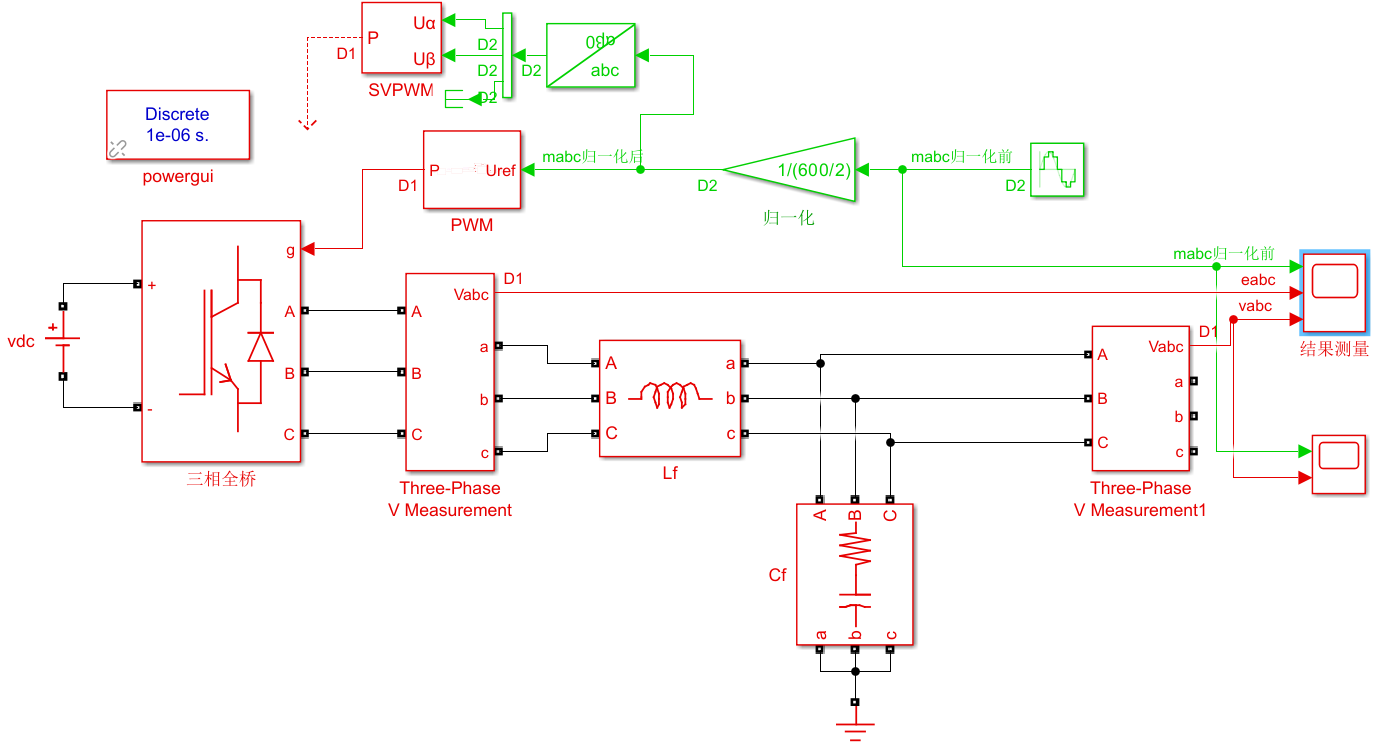
其中,主电路参数为:
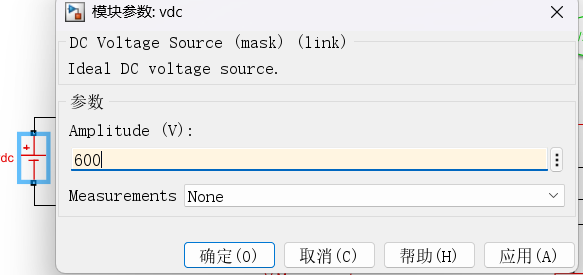
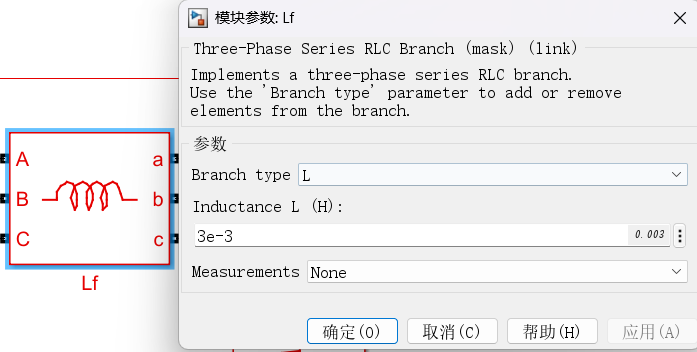
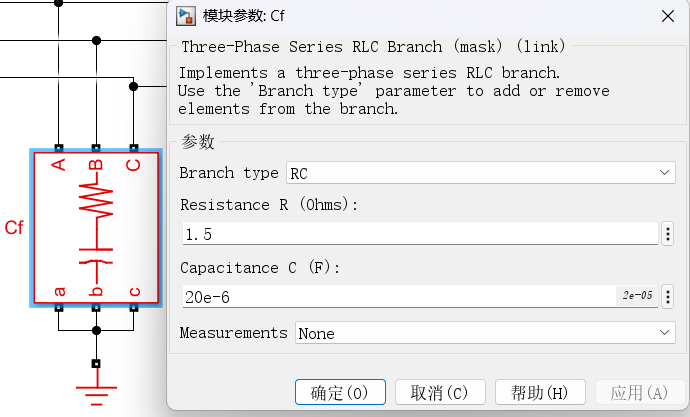
注:LC滤波器的转折频率近似为1/[ sqrt(3e-3*20e-6)*2*pi ]=650Hz;Cf串联一个小电阻是为了削弱LC滤波器在转折频率处的谐振峰,如下图所示:
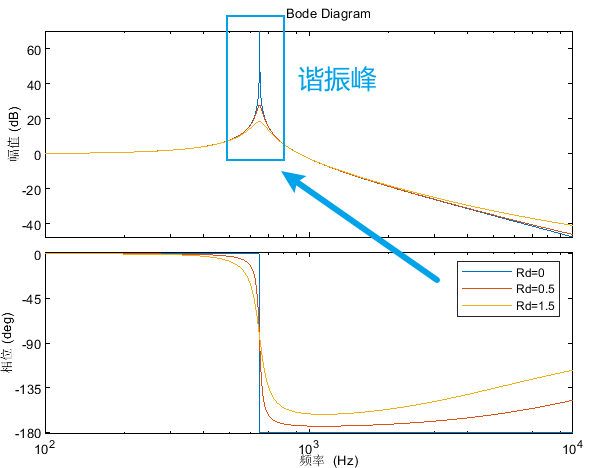
控制参数为:
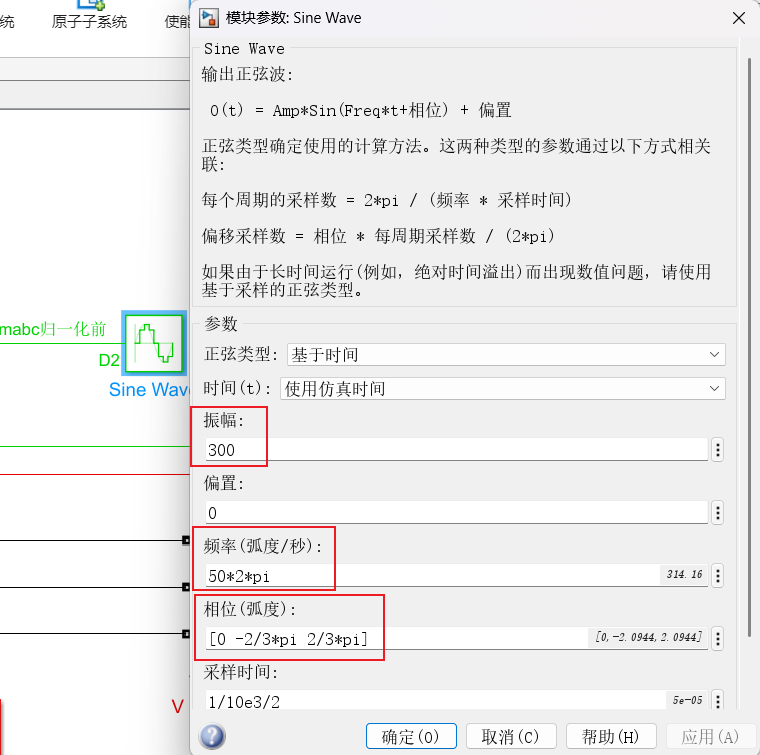
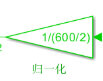
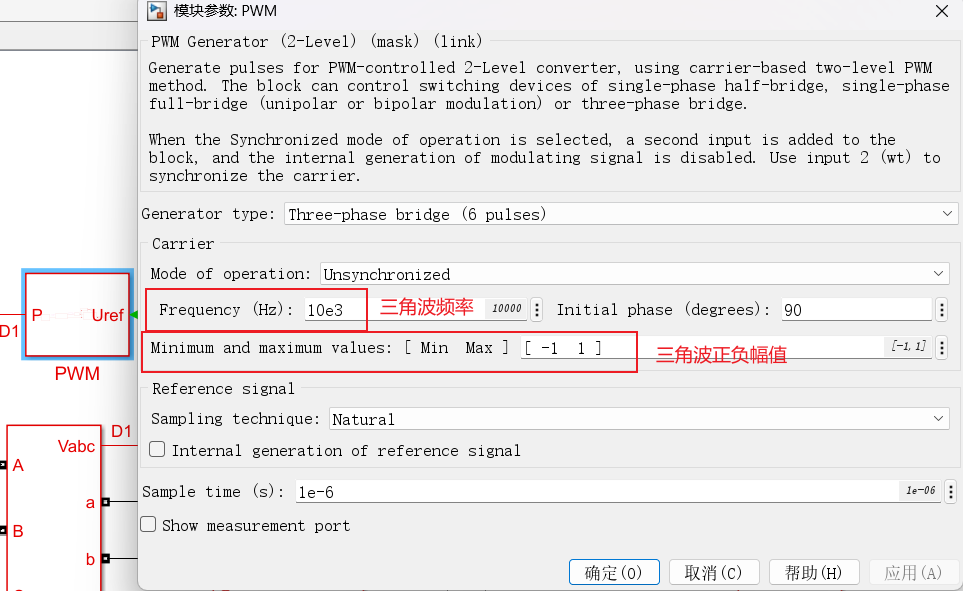
2.2 仿真结果
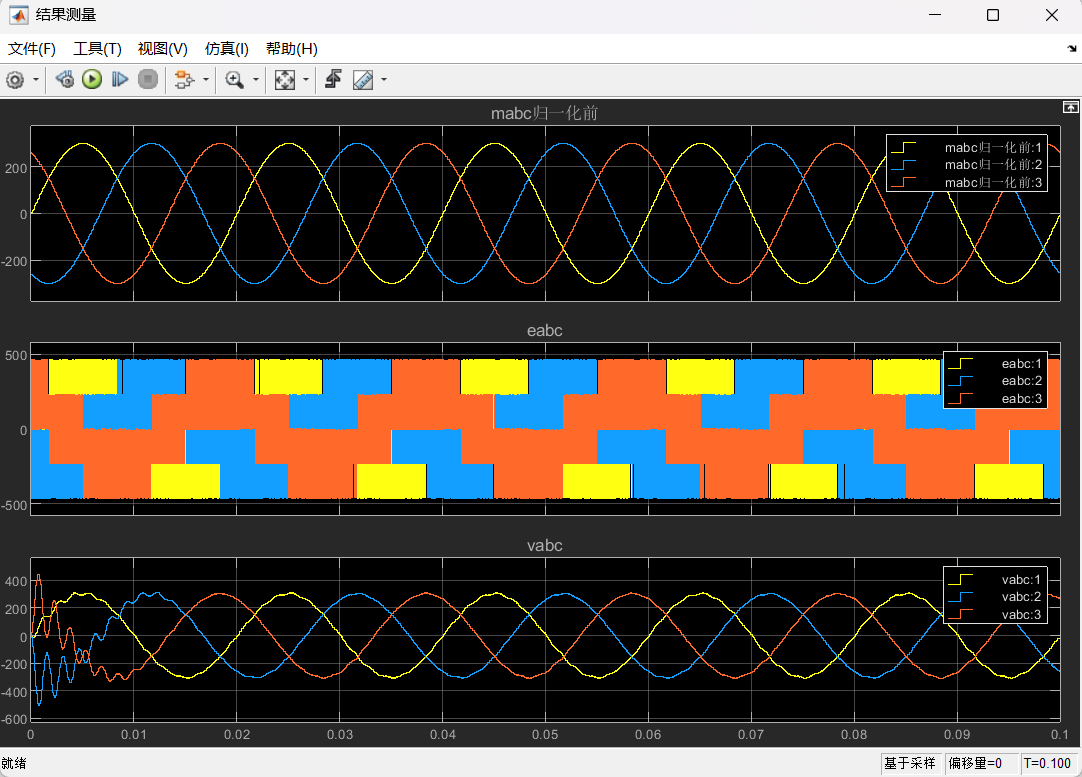
对Va(bc)N进行FFT分析(见文章如何利用matlab自带的函数及工具箱对信号进行频谱分析),得到VaN的频谱如下:
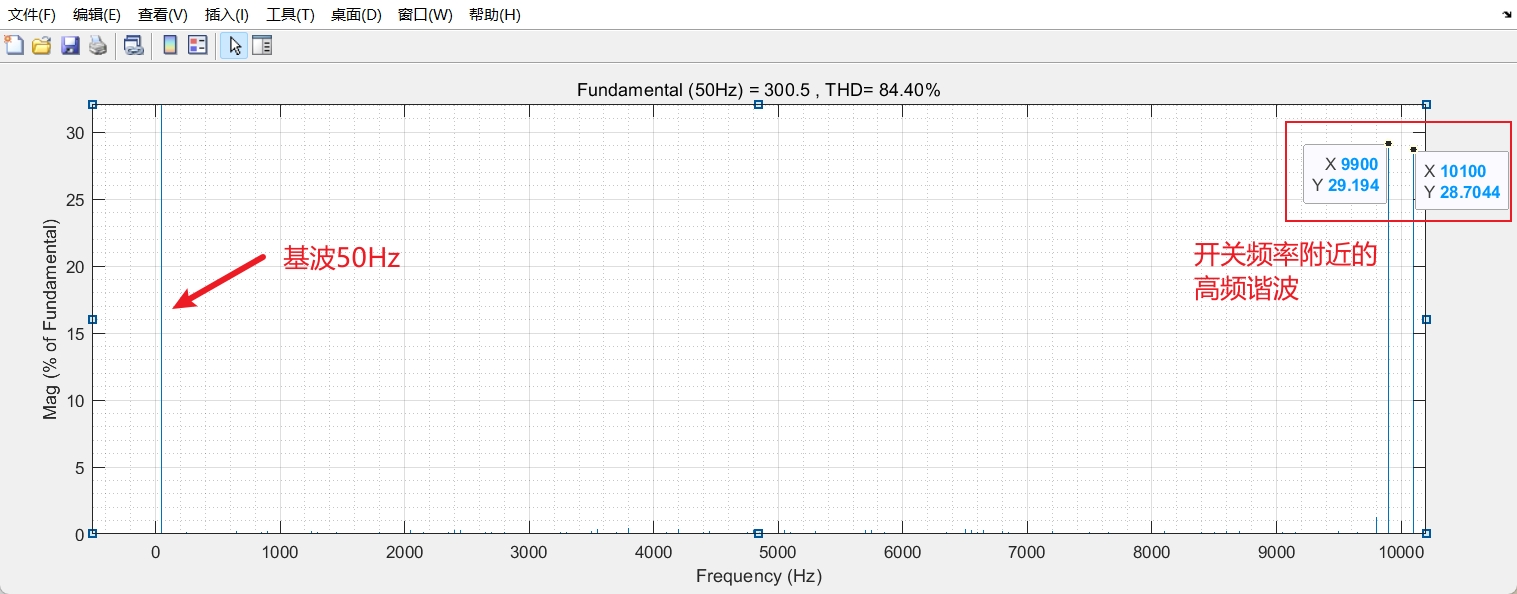
可见,VaN的谐波频率主要集中在fsw±2f1附近;Vb(c)N类似。
Va(bc)N基波分量eabc的基本信息如下:
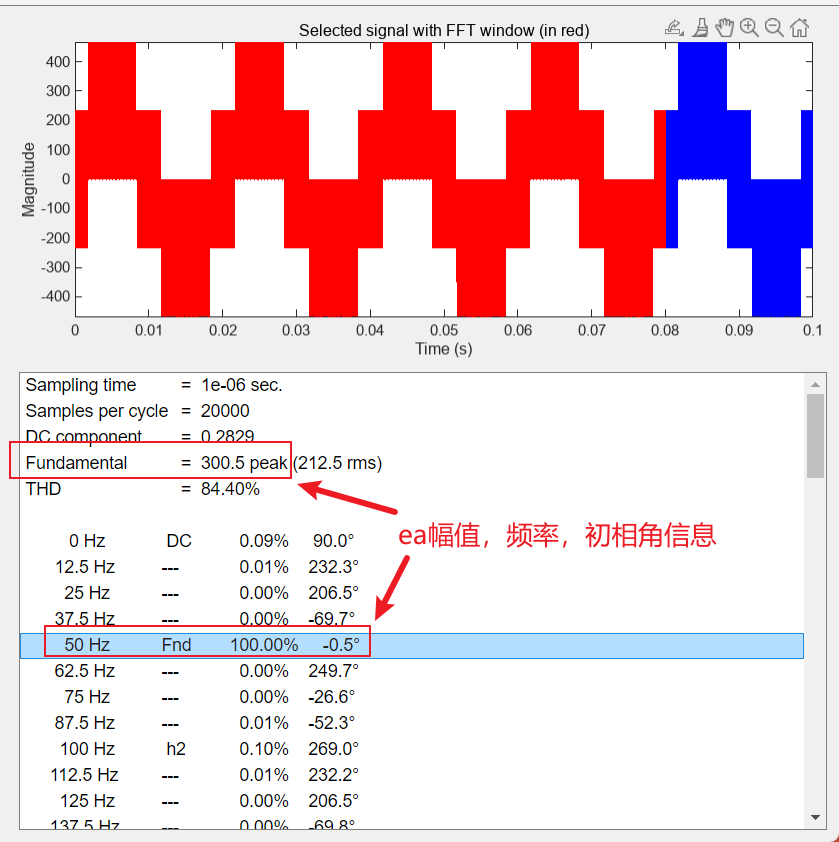
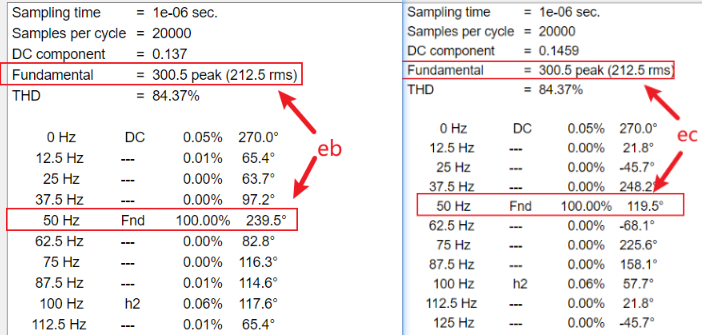
可见,eabc的幅值、频率和初相角与归一化前的mabc设置的参数基本保持一致,即eabc=归一化前的mabc,与理论分析保持一致。
对比一下归一化前的mabc和经LC滤波后的vabc信号,如下:
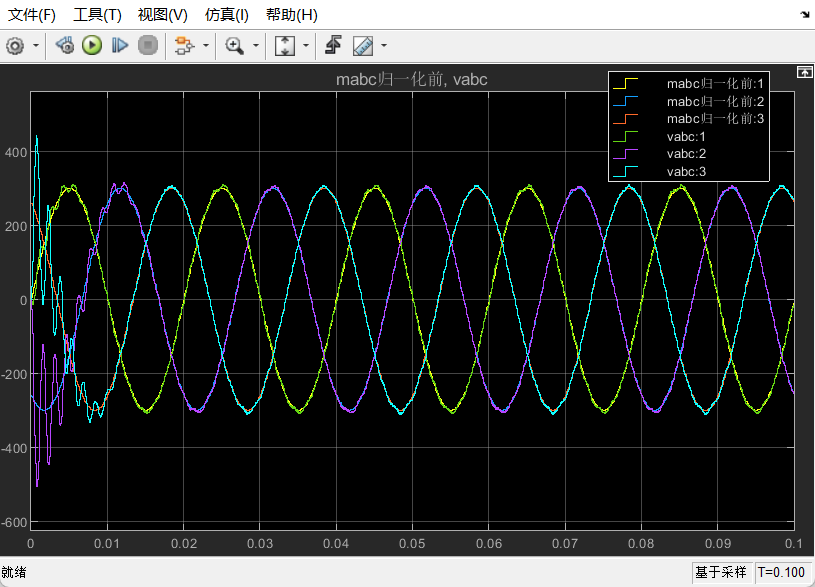
其中,Va的FFT结果如下:
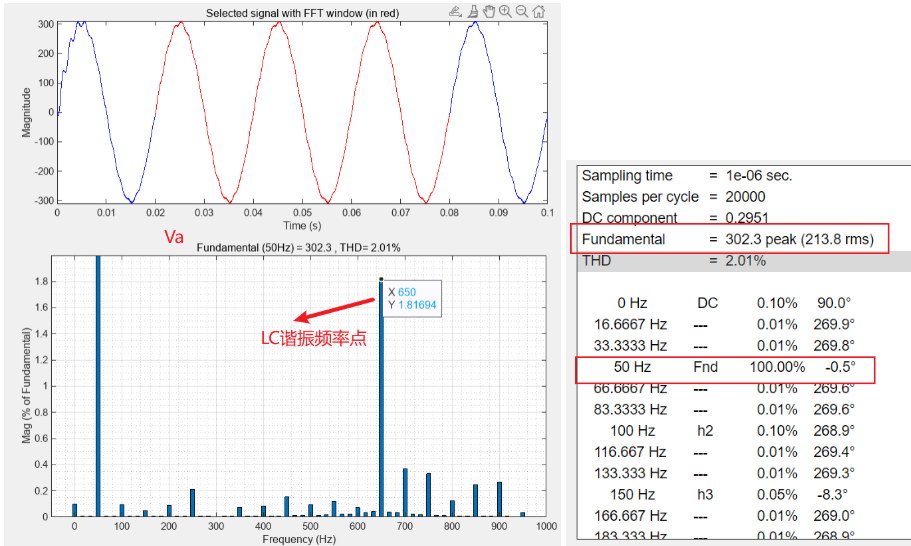
从vabc频谱图来看,va(bc)N中的基波分量基本不受影响;谐波分量基本被LC滤波器滤除了,只在转折频率处由于谐振峰的存在含有一定谐波。
将调制方式设置成SVPWM,观察ea的最大幅值:
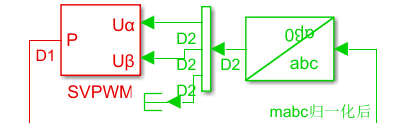
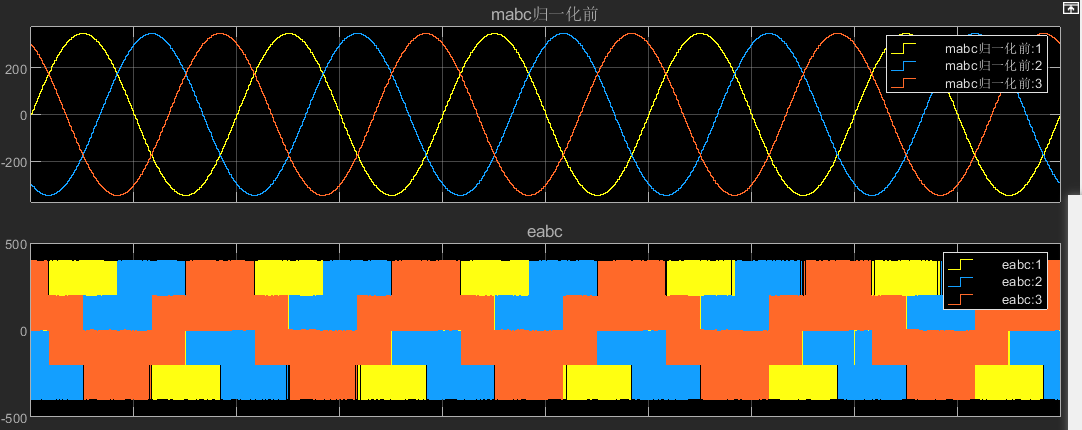
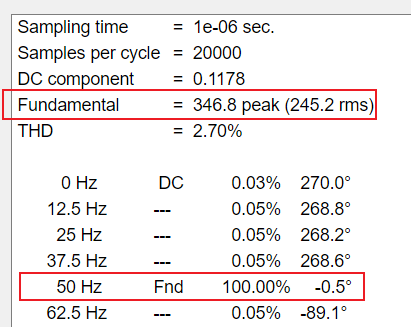
可见,相电压最大幅值可达2/sqrt(3)*vdc/2V,直流电压利用率为[2/sqrt(3)*vdc/2]*sqrt(3)/vdc =1。
3 总结
本文从理论和仿真两方面较为细致地分析了PWM的原理,分析表明:通过调制波如果以变流器输出内电势基波分量最大幅值为基准进行归一化,并将三角载波幅值设置为1,那么在PWM的线性调制区内,内电势基波分量eabc将与归一化前的调制波保持一致。另外,LC滤波器的转折频率和谐振峰的阻尼是影响滤波器效果的两个关键因素。
以上就是本文全部内容啦!系列内容持续更新中,未完待续!觉得有用还请多多支持一下吧,支持越多更新越快哟。
关注同名WX后台回复【矢量控制】即可获取本文模型,关注还可查看更多精彩内容哟。
