当前位置：首页 > news >正文

梯度下降与反向传播

news 2025/7/17 7:32:24

1.梯度下降

梯度下降就像你在一个浓雾笼罩的山坡上找下山的路。你看不清整个山的形状，但可以感觉到脚下的坡度。这时候，你会一步一步往坡度最陡的方向走，直到走到山脚。在机器学习中，这座“山”就是模型的误差（或损失），而“下山”就是找到让误差最小的参数。

举个生活例子：
假设你做饭时想调出最咸淡适中的汤，但不知道放多少盐。你每次尝一口，如果太淡就加盐（误差大时多调），如果快咸了就少加盐（误差小时微调）。梯度下降就是这种“尝汤→调整”的自动化版本。

关键点：

梯度：告诉你“误差变小的方向”（哪边坡度更陡）。
学习率：决定“一步迈多大”（步子太大会错过山脚，太小会走太慢）。
迭代：反复调整，直到误差不再明显下降。

简而言之，梯度下降是机器学习的“导航仪”，帮模型在复杂问题中找到最优解。

我先给大家po一道例题

我们首先看官方答案接下来我们进行仔细分析，首先我们要理解题意：

问题描述

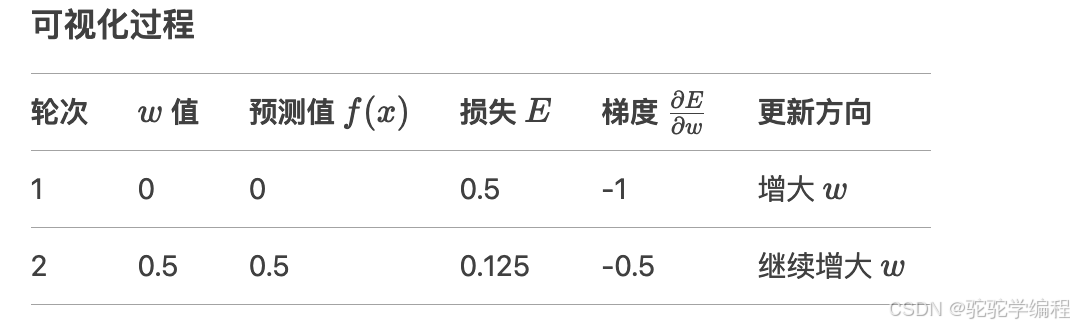
目标：通过梯度下降求解线性函数 f(x)=wx，使得 f(1)=1。

损失函数：E=1/2(wx−t)^2（均方误差）

参数：初始权重 w=0，学习率 η=0.5

输入与目标：x=1，t=1

梯度下降的核心步骤

梯度下降通过以下公式更新参数：
w←w−η⋅∂E/∂w
其中，∂E/∂w 是损失函数对权重 w 的梯度。

梯度下降通过以下步骤逐步优化参数：

计算预测值 → 2. 评估误差 → 3. 计算梯度 → 4. 沿负梯度方向更新参数。

第一轮训练（Epoch 1）

前向计算：
f(x)=w⋅x=0⋅1=0

计算损失：
E=1/2(0−1)^2=1/2⋅1=0.5

计算梯度：
∂E/∂w=x⋅(wx−t)=1⋅(0−1)=−1

更新权重：
w←0−0.5⋅(−1)=0.5

第二轮训练（Epoch 2）

前向计算：
f(x)=0.5⋅1=0.5

计算损失：
E=1/2(0.5−1)^2=1/2⋅0.25=0.125

计算梯度：
∂E/∂w=1⋅(0.5−1)=−0.5

更新权重：
w←0.5−0.5⋅(−0.5)=0.5+0.25=0.75

关键分析

梯度计算原理：
梯度 ∂E/∂w 反映了权重 w 对误差的影响方向。

当梯度为负（如第一轮的 −1），说明增大 w 可以减小误差。

当梯度为负（如第二轮的 −0.5），同理需继续增大 w。

学习率的作用：

学习率 η 控制参数更新的步长。

若 η 过大（如 η=1.5 ），可能导致权重在最优值附近震荡甚至发散。

若 η 过小（如 η=0.1 ），收敛速度缓慢。

本题中 η=0.5 是合理选择，两轮后 w 从 0 → 0.5 → 0.75，逐步逼近最优解 w=1。

损失函数的变化：

第一轮损失 E=0.5，第二轮 E=0.125，误差明显减小，说明梯度下降有效。

可能大家还是很难理解是什么意思，为什么要用这些公式，多次调整以后又会怎样，我给大家分享一下我看到过的一个通俗易懂的例子。

权重是什么？

权重就像“调节旋钮”，决定了不同输入对结果的影响大小。

例子：预测考试成绩时，学习时间和睡眠时间都可能影响分数。权重就是告诉你“学习时间更重要”还是“睡眠时间更重要”。比如，学习时间的权重是0.7，睡眠时间是0.3，说明学习对成绩的影响更大。

权重是怎样调整的？

调整权重就像“试错学习”：

预测：用当前权重算出一个结果（比如预测成绩80分）。

对比：看看和真实结果（比如实际成绩85分）差多少。

修正：如果预测低了，就调高相关权重；如果高了，就调低。

关键：系统自动计算“哪个旋钮该往哪边转，转多少”，让下次预测更准。

输入x和目标t是什么？

输入x：你给模型的数据，比如学习时间（5小时）、睡眠时间（8小时）。

目标t：你希望模型输出的正确答案，比如实际考试成绩（85分）。

任务：模型的任务是通过x猜出t，比如根据学习时间预测分数。

损失函数是什么？

损失函数就像“错误计分板”，告诉模型它猜得有多离谱。

计算方式：比如用预测值（80分）和真实值（85分）的平方差：
损失=(85−80)2=25损失=(85−80)2=25

目标：让这个“分数”越来越低，最终接近0（猜得完全正确）。

举个完整例子

场景：用学习时间预测考试成绩。

输入x：学习时间3小时 → 模型用权重w=2预测成绩：
预测成绩=3×2=6分预测成绩=3×2=6分

目标t：实际成绩是90分 → 损失：
(90−6)2=7056(90−6)2=7056

调整权重：

发现预测太低了，系统自动调高权重（比如w从2变成10）。

下次预测：3小时 × 10 = 30分 → 损失还是大，继续调整。

反复调整，直到预测接近90分。

总结

权重：决定输入对结果的影响程度，像“音量调节器”。

调整权重：通过不断试错，让预测一步步逼近正确答案。

输入x和目标t：x是问题（比如学习时间），t是答案（比如考试成绩）。

损失函数：量化预测的错误程度，目标是让它越来越小。

一句话理解：模型像学生，权重是它的“知识”，通过不断做题（调整权重）减少错误（损失），最终学会正确答案（目标t）。

2.反向传播

同样我想给大家先介绍一下什么叫反向传播及其为什么需要反向传播：

反向传播就像“错误纠正老师”在批改作业。假设你有一份多层答案（比如数学题分步骤解答），老师从最终答案开始检查，发现哪里错了，然后一步步往前找原因，告诉每个步骤应该怎么改。在神经网络中，这个“老师”会从输出层开始，逐层计算每个权重（参数）对总误差的“责任”，并告诉它们该调整多少。

高效找错：
神经网络可能有几百层，手动计算每一层对误差的影响几乎不可能。反向传播自动完成这个复杂任务，像用计算器快速算账。

例子：如果你做菜难吃，反向传播能告诉你到底是盐放多了，还是火候不对，而不需要你瞎猜。

精准调整：
它精确计算每个权重该调大还是调小，而不是随机乱调。

比喻：导航软件不仅告诉你“方向错了”，还会说“向左转30度”而不是“随便拐”。

讲到反向传播，我们还需要了解一下它与我们前面讲的梯度下降有什么关系：

反向传播和梯度下降的关系

分工合作：

反向传播：负责“算账”——计算每个权重该调整多少（梯度）。

梯度下降：负责“执行”——按照计算结果更新权重。

比喻：反向传播是财务部算出公司亏损的原因（哪个部门花钱多），梯度下降是CEO砍预算。

配合流程：

前向传播：网络做出预测（比如猜图片是猫还是狗）。

计算误差：比较预测和真实答案的差距。

反向传播：从输出层开始，逐层计算各权重的“责任”。

梯度下降：用这些责任值（梯度）调整权重，减少误差。

举个生活例子

场景：教机器人调咖啡甜度。

目标：让咖啡甜度刚好（比如糖量=5克）。

反向传播：

机器人第一次放了3克糖（误差=2克）。

反向传播告诉它：“误差是2克，是因为你糖罐每次倒的量少了，应该多倒0.5克。”（你想想，这时候学习率就起作用了）

梯度下降：
机器人根据反馈调整糖罐阀门，下次倒3.5克。
反复几次后，误差越来越小，最终学会倒5克。

了解完他们之间的关系后，我还是po一道例题来进行讲解

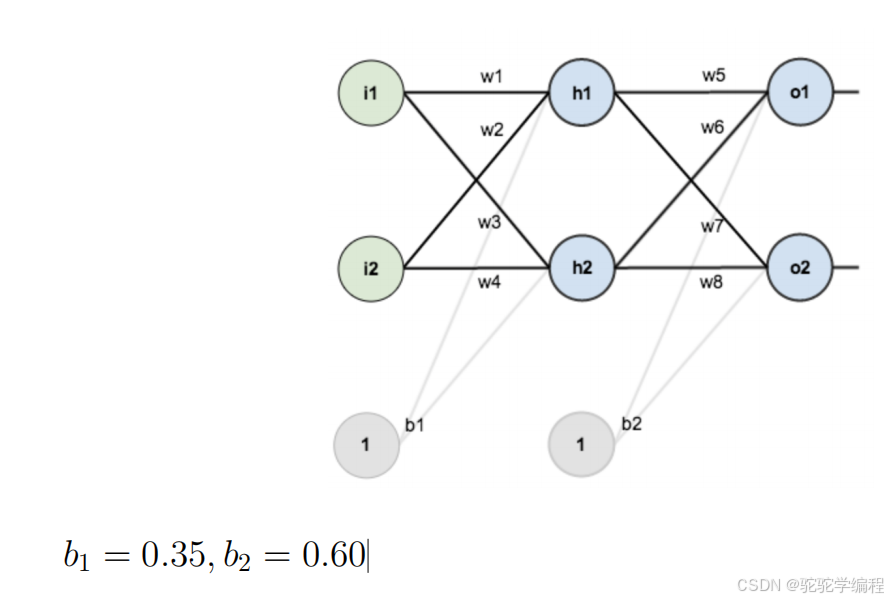
b1 = 0.35, b2 = 0.60 接下来我们还是先分析题意

网络结构

输入层：i1=0.05, i2=0.10

隐藏层：2个神经元（使用Sigmoid激活）

输出层：2个神经元（使用Sigmoid激活）

目标值：outo1=0.01, outo2=0.99

初始权重与偏置：
w1=0.15, w2=0.20, w3=0.25, w4=0.30,w5=0.40, w6=0.45, w7=0.50, w8=0.55,b1=0.35, b2=0.60.

首先我来解释一下这些专有名词以及常见的问题：

1.隐藏层是什么？

隐藏层就像厨房里的“切菜工”，负责把原始食材（输入数据）处理成厨师（输出层）能直接使用的形状。

例子：做披萨时，输入是面团和配料，隐藏层负责把面团擀平、切好蔬菜，输出层把这些半成品组装成披萨。

作用：提取数据的关键特征，比如从图片中识别边缘、颜色，再让输出层判断是不是猫。

2.目标值是什么？

目标值是你希望模型给出的“标准答案”。

例子：教小孩认动物时，你指着猫说“这是猫”，目标值就是“猫”。

在题目中：输入是 i1=0.05, i2=0.10，目标值是 outo1=0.01, outo2=0.99，表示希望输出层第一个神经元接近0.01，第二个接近0.99。

3.为什么有这么多权重？

权重决定了不同输入对结果的影响程度，就像水管上的“阀门”，控制水流大小。

输入层→隐藏层：每个输入节点连接到每个隐藏节点，形成多个“阀门”。

比如输入层2个节点，隐藏层2个节点 → 需要4个权重（w1~w4）。

隐藏层→输出层：同理，每个隐藏节点连接到每个输出节点 → 再加4个权重（w5~w8）。

总权重数：输入层到隐藏层4个 + 隐藏层到输出层4个 = 8个权重。

作用：通过调整这些“阀门”，让模型更灵活地学习复杂关系。

4.偏置是干什么的？

偏置像“保底分数”，即使所有输入为零，神经元也能有一定输出。

例子：考试卷面分是0，但老师可能给每个学生加10分“平时分”，这10分就是偏置。

在题目中：

隐藏层偏置 b1=0.35：保证隐藏神经元至少有一定激活值。

输出层偏置 b2=0.60：同理，调整输出的基准值。

作用：提高模型灵活性，防止输入全为零时神经元“死机”。

举个完整例子

任务：用神经网络判断明天是否下雨（输出1=下雨，0=不下雨）。

输入层：温度（25℃）、湿度（80%）→ 两个节点。

隐藏层：

提取特征，比如“湿度高且温度低容易下雨”。

权重 w1 控制温度对“下雨可能性”的影响，w2 控制湿度的影响。

输出层：综合隐藏层的信息，给出最终预测（比如0.7，表示70%可能下雨）。

目标值：如果实际下雨了，目标值就是1。

偏置：即使温度和湿度都是0，偏置也能让模型认为“可能有其他因素导致下雨”。

总结

隐藏层：数据加工的中间站，提取有用特征。

目标值：模型需要逼近的标准答案。

权重数量：每个连接都有独立“阀门”，越多模型越灵活。

偏置：保底调整项，防止模型僵化。

一句话理解：神经网络像多级流水线，权重是调节阀，偏置是保底分，目标值是质检标准，隐藏层是中间加工环节，共同协作产出合格产品。

反向传播的处理共分为三个步骤：

前向传播：通过加权和与激活函数逐层计算输出。

反向传播：从输出层开始，利用链式法则逐层计算误差梯度。

更新参数：根据梯度和学习率调整权重和偏置，使损失函数最小化。

我列举出计算中需要用到的所有公式（就本题而言）：

根据这些公式，我们可以开始进行运算：

同理，我来解释一下比较难以理解的点：

1.Sigmoid激活函数的作用

通俗解释：
Sigmoid函数就像一个“压缩器”，把神经元的输入信号变成一个0到1之间的数。比如，输入信号很大时，输出接近1，表示“可能性很高”；输入信号很小时，输出接近0，表示“可能性很低”。

为什么需要它：
没有它，神经网络就像一台只会做加减法的机器，无法处理复杂问题。Sigmoid让网络能“灵活思考”，比如判断图片是猫还是狗。

2.字符含义

通俗理解

权重（w）：像水管上的阀门，控制信息流动的强弱。

偏置（b）：像考试中的“平时分”，保证神经元最低活跃度。

激活函数（σ）：像过滤器，把原始信号变成0-1的概率值。

损失（E）：像成绩单，分数越低说明模型越聪明。

梯度（δ）：像导航箭头，告诉模型该往哪个方向调整参数。

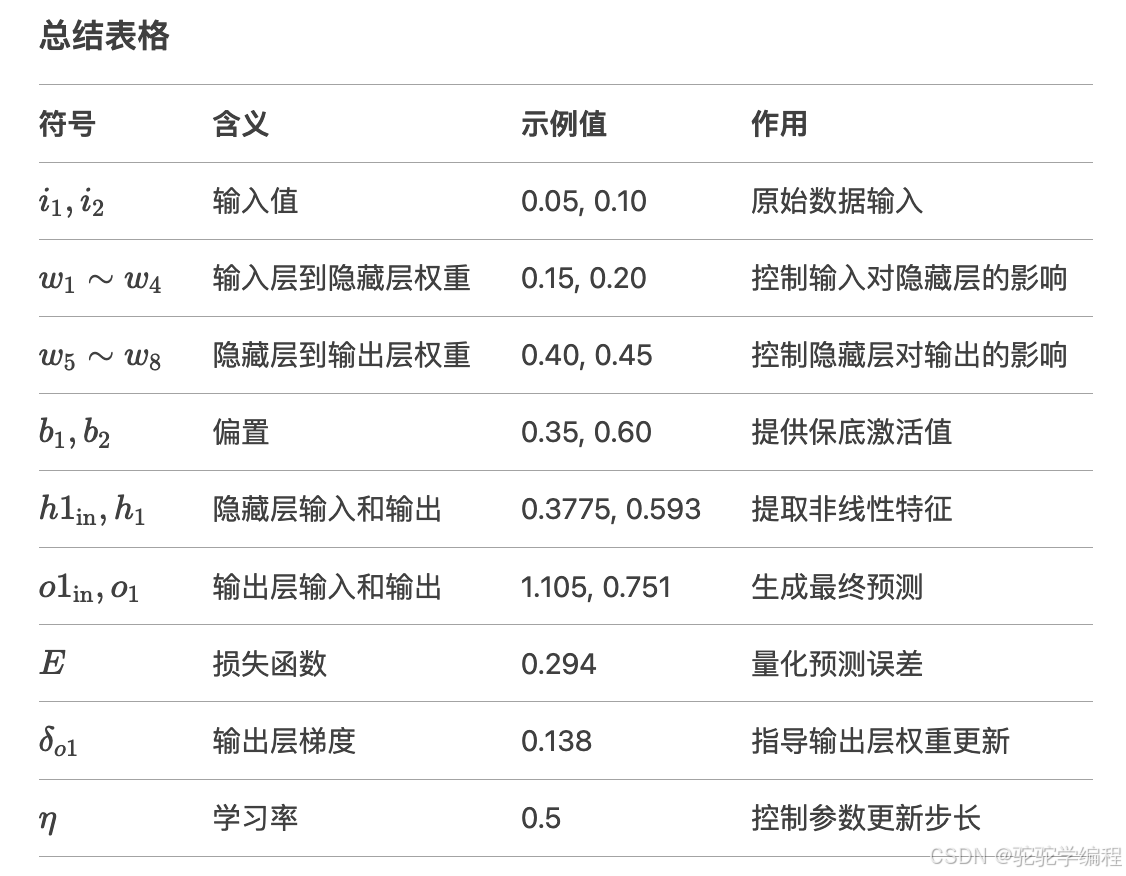
3.剖析符号及公式

a. 输入层符号

i1,i2

含义：输入特征值，即模型接收的原始数据。

示例：在题目中，i1=0.05，i2=0.10。

作用：类似“食材”，是模型加工的起点。

b. 权重符号

w1,w2,w3,w4

含义：输入层到隐藏层的连接权重。

示例：w1=0.15 表示第一个输入 i1 对隐藏层第一个神经元的“重视程度”。

作用：控制输入对隐藏层的影响大小，类似“音量调节旋钮”。

w5,w6,w7,w8

含义：隐藏层到输出层的连接权重。

示例：w5=0.40 表示隐藏层第一个神经元 h1 对输出层第一个神经元 o1 的贡献比例。

作用：决定隐藏层特征如何影响最终输出。

3. 偏置符号

b1

含义：隐藏层的偏置项。

示例：b1=0.35。

作用：即使所有输入为零，隐藏层神经元也能有一定激活值，类似“保底分数”。

b2

含义：输出层的偏置项。

示例：b2=0.60。

作用：调整输出层的基准值，避免输出僵化。

4. 隐藏层符号

h1in,h2in

含义：隐藏层神经元的输入（未激活的值）。

计算公式：
h1in=w1i1+w2i2+b1

作用：类似“未加工的食材”，需经过激活函数处理。

h1,h2

含义：隐藏层神经元的输出（激活后的值）。

计算公式：
h1=σ(h1in)

作用：提取输入数据的非线性特征，类似“半成品”。

5. 输出层符号

o1in,o2in

含义：输出层神经元的输入（未激活的值）。

计算公式：
o1in=w5h1+w6h2+b2

作用：综合隐藏层信息，准备生成最终输出。

o1,o2

含义：输出层神经元的最终预测值（激活后的值）。

计算公式：
o1=σ(o1in)

作用：模型的预测结果，例如分类概率或回归值。

6. 损失函数符号

E

含义：均方误差（Mean Squared Error, MSE），衡量预测值与目标值的差距。

计算公式：
E=1/2[(o1−outo1)^2+(o2−outo2)^2]

作用：量化模型的错误程度，是优化的目标。

7. 误差梯度符号

δo1,δo2

含义：输出层神经元的误差梯度，表示输出层对总误差的“责任”。

计算公式：
δo1=(o1−outo1)⋅o1(1−o1)

作用：指导输出层权重的调整方向和幅度。

δh1,δh2δh1,δh2

含义：隐藏层神经元的误差梯度，表示隐藏层对总误差的“责任”。

计算公式：
δh1=(δo1⋅w5+δo2⋅w7)⋅h1(1−h1)

作用：指导隐藏层权重的调整方向和幅度。

8. 更新公式中的符号

η

含义：学习率（Learning Rate），控制参数更新的步长。

示例：η=0.5 表示每次更新参数时，按梯度方向的50%调整。

作用：避免步子太大（震荡）或太小（收敛慢）。

h1,h2,i1,i2

来源：前向传播中计算得到的中间值（如 h1=σ(h1in)）。

作用：在反向传播中，用于计算权重更新的具体数值。例如：
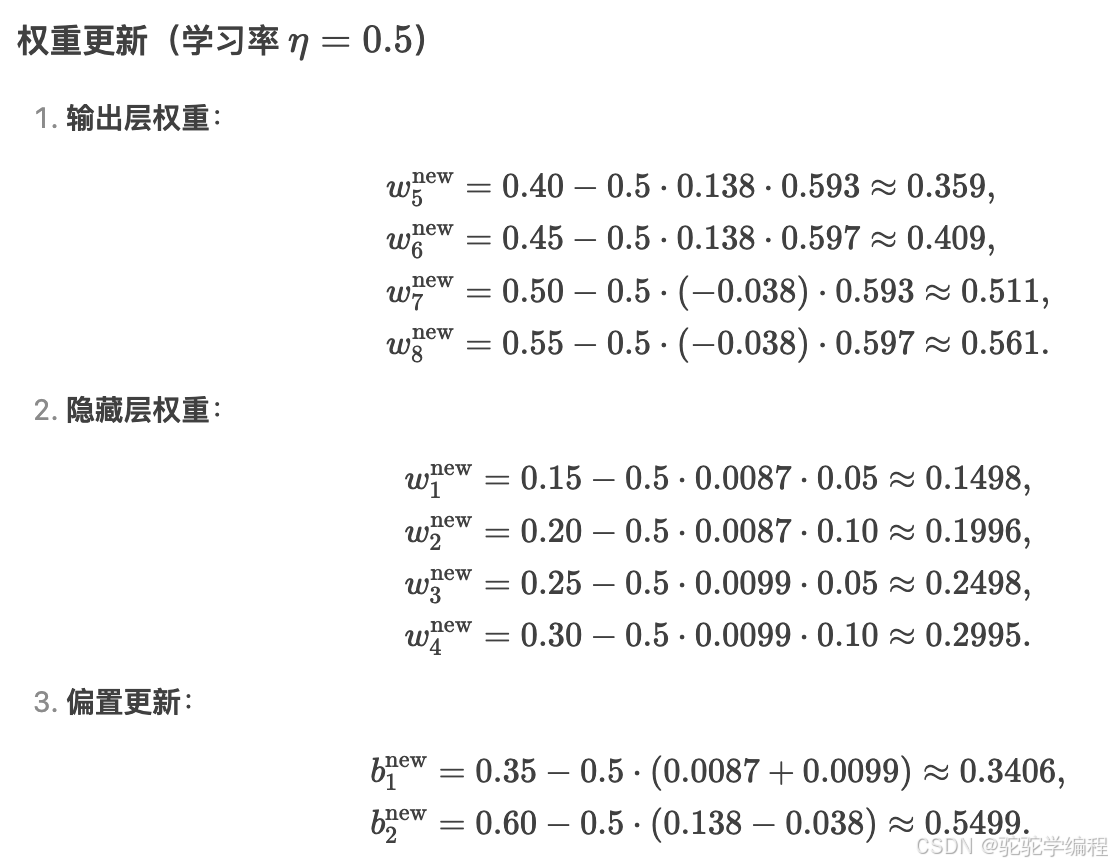
w5new=w5−η⋅δo1⋅h1