模型剪枝详解（一）：认识剪枝

模型剪枝详解（一）：认识剪枝

1. 背景

模型剪枝（Pruning）与蒸馏（KD）的目的是一样的都是为了缩小模型，进行模型压缩，来加速的一种技术方法。

知识蒸馏的文章可以翻一翻前面文章的详细介绍

1.1 什么是剪枝

剪枝是把对最终任务贡献很小的参数/通道/层删除，使模型更小、更快、更省电，同时尽量不掉精度。常见收益：

• 参数/显存：降低模型大小、加载时间、显存占用。
• 吞吐/延迟：在结构化剪枝或特定稀疏格式支持下显著加速。
• 正则化：一定程度上还能缓解过拟合。

1.2 为什么可以剪枝

• 参数冗余： 实现发现，在大多数神经网络的训练中，权重稀疏现象普遍存在，所谓稀疏是指权重大部分在0值附近。而我们只知道权重为0，恰恰是最不重要的值。因此权重参数大多是冗余的，减少权重参数成为了可能。
• 经验事实：把一大批权重置零（非结构化）或删通道/头/层（结构化），经过少量微调，精度通常几乎不变。
• 就是因为这种深网普遍冗余、可稀疏化、可结构选择，且删掉一部分参数/结构对函数扰动可控，才让剪枝成为可能。

---

2. 剪枝分类

剪枝可分为两大类，一个是非结构化剪枝，另一个是结构化剪枝。

2.1 非结构化剪枝

从字面意思很好理解，非结构化是不改变模型结构和参数的，而是将模型的一些参数设置为0。而这种剪枝实际上对模型提速有限，因为模型参数量是没有变的，只是有用参数减少了。如今实际应用很少，因为达不到真正加速。

看一个代码示例：

import torch  
import torch.nn as nn  
import torch.nn.utils.prune as prune  def global_unstructured_l1(model: nn.Module, amount: float = 0.5, remove: bool = False):  """对 Conv/Linear 的 weight 做全局 L1 非结构化剪枝。  amount=0.5 表示全局 50% 权重置零；remove=False 时保留 mask 以便微调。"""  params_to_prune = []  for m in model.modules():  if isinstance(m, (nn.Conv2d, nn.Linear)):  params_to_prune.append((m, "weight"))  prune.global_unstructured(  params_to_prune,  pruning_method=prune.L1Unstructured,  amount=amount,  )  if remove:  for m, _ in params_to_prune:  prune.remove(m, "weight")   # 固化并移除mask  class MLP(nn.Module):  def __init__(self):  super().__init__()  self.net = nn.Sequential(  nn.Flatten(),  nn.Linear(28*28, 300),  nn.ReLU(),  nn.Linear(300, 100),  nn.ReLU(),  nn.Linear(100, 10),  )  def forward(self, x): return self.net(x)  def report_sparsity(model: nn.Module, show_layers=True):  total, zeros = 0, 0  for name, m in model.named_modules():  if isinstance(m, (nn.Conv2d, nn.Linear)):  w = m.weight.detach()  z = (w == 0).sum().item()  n = w.numel()  total += n; zeros += z  if show_layers:  print(f"{name:30s}  weight sparsity: {z/n:6.2%} ({z}/{n})")  print(f"GLOBAL weight sparsity: {zeros/total:6.2%} ({zeros}/{total})")  def fold_masks(model: nn.Module):  for m in model.modules():  if isinstance(m, (nn.Conv2d, nn.Linear)) and hasattr(m, "weight_mask"):  prune.remove(m, "weight")   # 权重中保留0，移除mask与reparam  model = MLP()  
global_unstructured_l1(model, amount=0.8)  print("After pruning (mask active, not removed):")  
report_sparsity(model)  # 微调  
# ...  # 微调之后删除"weight_mask"  
fold_masks(model)  print()

在调用fold_masks(model) 之前打个断点看一下结果。
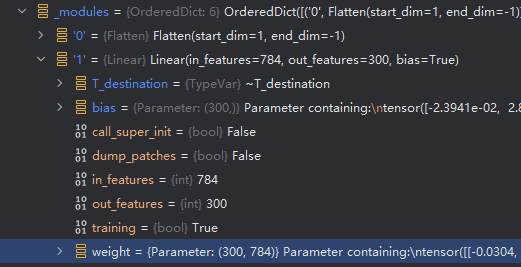
在调用global_unstructured_l1之后，有以下改变：

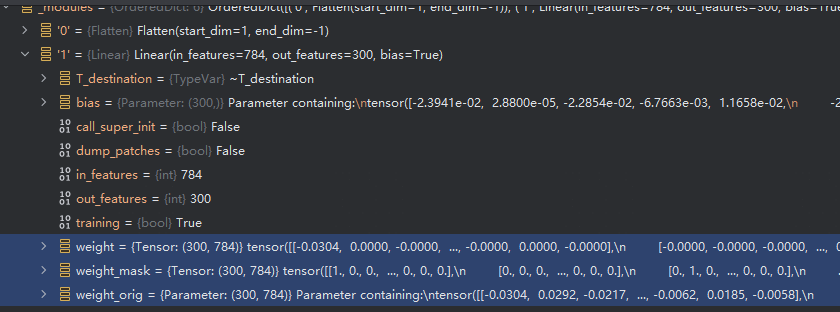
• 可以看到weight 大部分为0，且为0的地方为weight_mask
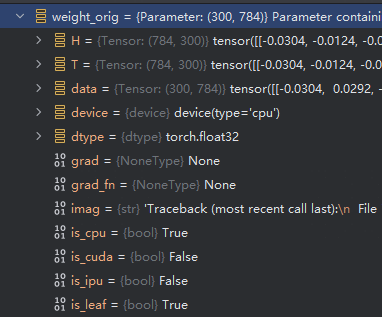
• weight_ori 为原始没被mask的参数，weight = weight_mask * weight_ori
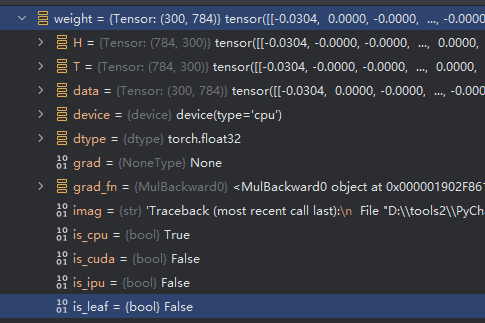
• weight_ori 是leaf 而weight已经不是leaf。而后续训练参数的更新，grad 也会被mask掉，weight_ori 才是被更新的参数，而weight只是计算后的结果。
  
  
  

---

看打印：
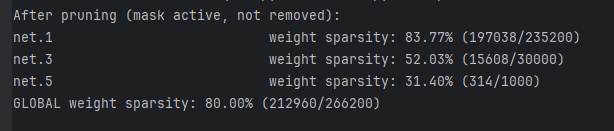
从打印来看，被置为0的参数确实是80%

---

remove 之后，debug看结果：
参数只剩下weight，并且叶子节点又回来了

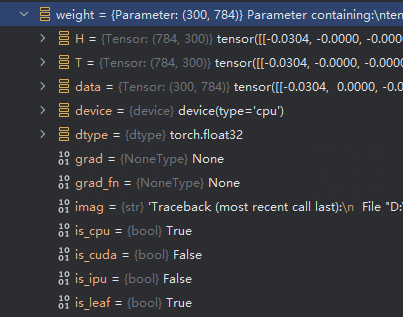
因此微调训练之前不能remov，因为remove之后，不在存在mask，而直接更新weight，会导致本来为0的地方重新回来了。违背了我们剪枝的本意。

2.2 结构化剪枝

把网络中一整块结构删掉，而不是把单个权重置零。典型粒度：

• Conv/Linear：删输出通道/输入通道（相当于删整列/整行）

• Transformer：删注意力头、缩小 FFN 中间维度、甚至删整层

• 更粗：删整个分支/Block

与非结构化不同，结构化剪枝会改变张量形状与计算图，因此：

• 一般能在常规 BLAS/GEMM/Conv 内核上获得真实加速、显存降低

• 但对精度更敏感，需要小步剪 + 微调/蒸馏

---

常见做法（两条线）

基于重要性评分的“删通道”：按每个通道的 L1/L2 范数、Taylor（|g·w|）、激活能量等打分，迭代删除得分最低的一部分，再微调。

1) 通道 L1 / L2 范数（weight-based）

定义：只看该通道对应的权重大小。
以 Conv2d(weight 形状 [C_out, C_in, kH, kW]) 为例，对输出通道 c 的分数：

• L1： $s_c={\sum }_{i,j,k}|W[c,i,j,k]|$

• L2： $s_c=\sqrt{{\sum }_{i,j,k}W[c,i,j,k{]}^2}$（很多实现直接用平方和不开方）

直觉：如果一个通道的权重整体很小，说明它对输出贡献可能也小 → 可剪。

优点：超快（只看权重），效果稳，是结构化剪枝最常用的基线。
缺点：不看数据/梯度，可能误删对特定输入分布重要但权重幅值偏小的通道。

---

2) Taylor 一阶（|g·w|，gradient × weight）

定义：用一阶泰勒展开估计“把某通道置零时，损失会增加多少”。
对该通道的所有权重 w 和它们的梯度 g：

$\Delta \mathcal{L}\approx \left|{\sum }_u{g}_u{w}_u\right|\text{（或逐元素取绝对后再和）}$

分数：$s_c=|⟨g_c,w_c⟩|$（通道内内积的绝对值）。

直觉：如果某通道的 $g\cdot w$ 小，说明把它压到 0 对损失的一阶影响小 → 更可剪。比纯幅值更贴近“对损失的敏感度”。

优点：考虑了梯度，通常比纯 L1/L2 更合理；只需要一次反向就能拿到 g。
缺点：需要在一个 batch/几个 batch 上跑前向+反向收集梯度；分数对 batch 选择较敏感。

---

3) 激活能量（activation-based / data-driven）

定义：看该通道在数据上的输出强度（不看梯度）。
设本层输出激活 A = conv(x)，形状 [N, C_out, H, W]，某通道 c 的分数可以是：

• 平均 L1：$s_c={\mathbb{E}}_{n,h,w}|A_{n,c,h,w}|$

• 或平均 L2：$s_c=\mathbb{E}\sqrt{{\sum }_{h,w}{A}_{n,c,h,w}^2}$

直觉：通道如果几乎不被激活（输出接近 0），对下游贡献小 → 可剪。它是基于数据分布的视角。

优点：反映真实数据上的“使用频率/强度”；不需要梯度。
缺点：需要跑一段校准数据收集统计；受输入分布影响大；激活为 0 也可能是“抑制”而非无用。

---

选哪个？怎么用？

• 起步/大多数场景：先用 L1/L2（快、稳）。
• 想更贴近损失：用 Taylor |g·w|（在校准 batch 上做一次 backward）。
• 数据分布很关键（如门控/稀疏激活网络）：加上 激活能量 做多指标融合（可线性加权或归一后取加权和）。

---

常见坑

• 维度搞错：Conv 输出通道看 dim=0，Linear 输出单元看 dim=0；输入通道则是另一维。

• Taylor 分数必须有梯度：别在 no_grad/验证阶段收集。

• 激活统计要代表部署分布：用校准数据；BN 层最好做一次 BN 重校准 后再评估。

• 一次剪太狠：迭代小步（10–30%）+ 微调更稳。

---

训练期诱导组稀疏：加 Group Lasso 或门控变量（可微/硬门）让某些通道自然收缩到 0，收敛后把接近 0 的整通道移除。

这是在训练阶段就主动“引导”网络学出整通道为 0（或几乎 0）的做法。等训练收敛后，你只需把这些“几乎为 0 的通道”整体删掉（改网络形状），就完成了结构化剪枝。

---

1) Group Lasso（组稀疏正则）

把一整组参数的范数（比如 Conv 的“一个输出通道就是一组”）加到损失里，鼓励整组一起变小到 0。

以 Conv2d 权重 W ∈ ℝ[C_out, C_in, kH, kW] 为例，对每个输出通道 cc 的组范数：

$$|W_c{\Vert }_2=\sqrt{\sum _{i,j,k}{W}_{c,i,j,k}^2}$$

整体正则项就是：

$${\mathcal{R}}_{\text{group}}(W)=\sum _{c=1}^{C_{\text{out}}}\Vert W_c{\Vert }_2$$

训练时最小化：

$$\underset{\theta }{\min }{\mathcal{L}}_{\text{task}}(\theta )+\lambda \sum _{\text{layers}}\sum _c\Vert W_c{\Vert }_2$$

当某些通道的 $\Vert W_c{\Vert }_2$ 被压得接近 0，它们的输出也会很弱——收敛后直接删除这些通道。

训练完之后：按照每层 $\Vert W_c{\Vert }_2$ 的大小设置阈值，把接近 0 的整通道删掉。

---

2) 门控变量（gating）：给每个通道一个“开关”

给每个输出通道引入一个可学习的标量门 $g_c$（乘在该通道的输出或权重上），并对 $g$ 加稀疏化正则（常用 L1；更激进可用 L0 的可微近似）。

• 结构：$y_c=g_c\cdot {\text{Conv}}_c(x)$
• 正则：$\mathcal{R}(g)=\alpha {\sum }_c|g_c|（L1）$，或 Hard-Concrete/L0 近似使 $g_c$真正稀疏到 0/1。
• 训练后很多 $g_c\approx 0$，直接把这些通道及其后续依赖删掉。

训练时：loss = task_loss + alpha * R(g), 训练收敛后：挑选 |gate| 很小的通道整体删除，并联动下游层
进阶：把 L1 换成 Hard-Concrete（Louizos et al., 2018）之类的 L0 近似，可得到更“硬”的 0/1 门；实现略复杂，这里给出直观易用的 L1 版本。

---

选哪个方法

• 想动改动最少、实现快：Group Lasso（几行正则 + 阈值 + 改结构）
• 想控制更直接、可解释：门控（门=通道重要性），还能做稀疏度调度/硬门
• 两者可以结合：先加门控，再对权重加 Group Lasso/Weight Decay，效果更稳

---

对比一下两条路线：

---

接下俩我给出了第一条路线的一个示例代码：

import torch  
import torch.nn as nn  
import torch_pruning as tp  class TinyCNN(nn.Module):  def __init__(self):  super().__init__()  self.conv1 = nn.Conv2d(3, 32, 3, padding=1)  self.bn1   = nn.BatchNorm2d(32)  self.conv2 = nn.Conv2d(32, 64, 3, padding=1)  self.bn2   = nn.BatchNorm2d(64)  self.pool  = nn.AdaptiveAvgPool2d((8,8))  self.head  = nn.Linear(64*8*8, 10)  self.act   = nn.ReLU()  def forward(self, x):  x = self.act(self.bn1(self.conv1(x)))  x = self.act(self.bn2(self.conv2(x)))  x = self.pool(x).flatten(1)  return self.head(x)  model = TinyCNN().eval()  
print("剪枝前：", model, sep="\n")  example_inputs = torch.randn(1, 3, 32, 32)  importance = tp.importance.MagnitudeImportance(p=1)   # L1  
ignored_layers = [model.head]                            pruner = tp.pruner.MagnitudePruner(  model,  example_inputs=example_inputs,  importance=importance,  global_pruning=False,      # 每层按比例  pruning_ratio=0.30,        # 删 30% 输出通道  ignored_layers=ignored_layers,  
)  pruner.step()  # 执行一次剪枝（也可以多轮：循环 step() + 微调）  print("剪枝后：", model, sep="\n")

运行结果，可以看到，模型通道数确实会减少很多。

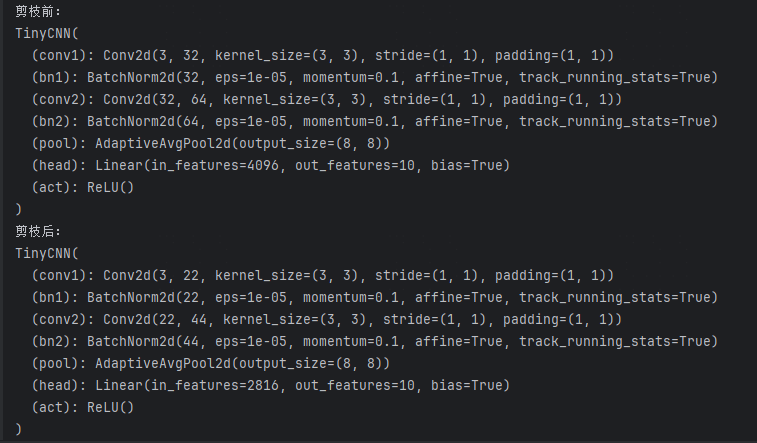
工程领域一般选结构化剪枝，因为结构化剪枝才是真正的缩小模型

3 微调（常搭配蒸馏）

简短结论：多数情况下建议用蒸馏来微调（finetune）剪枝后的模型，尤其是**结构化剪枝、剪得比较狠（>20–30% 通道/头）**或者你的数据不算很大时。轻度剪枝（<10–15%）常规微调也能收回大部分精度。