2025年--Lc188--221. 最大正方形(多维动态规划,矩阵）--Java版

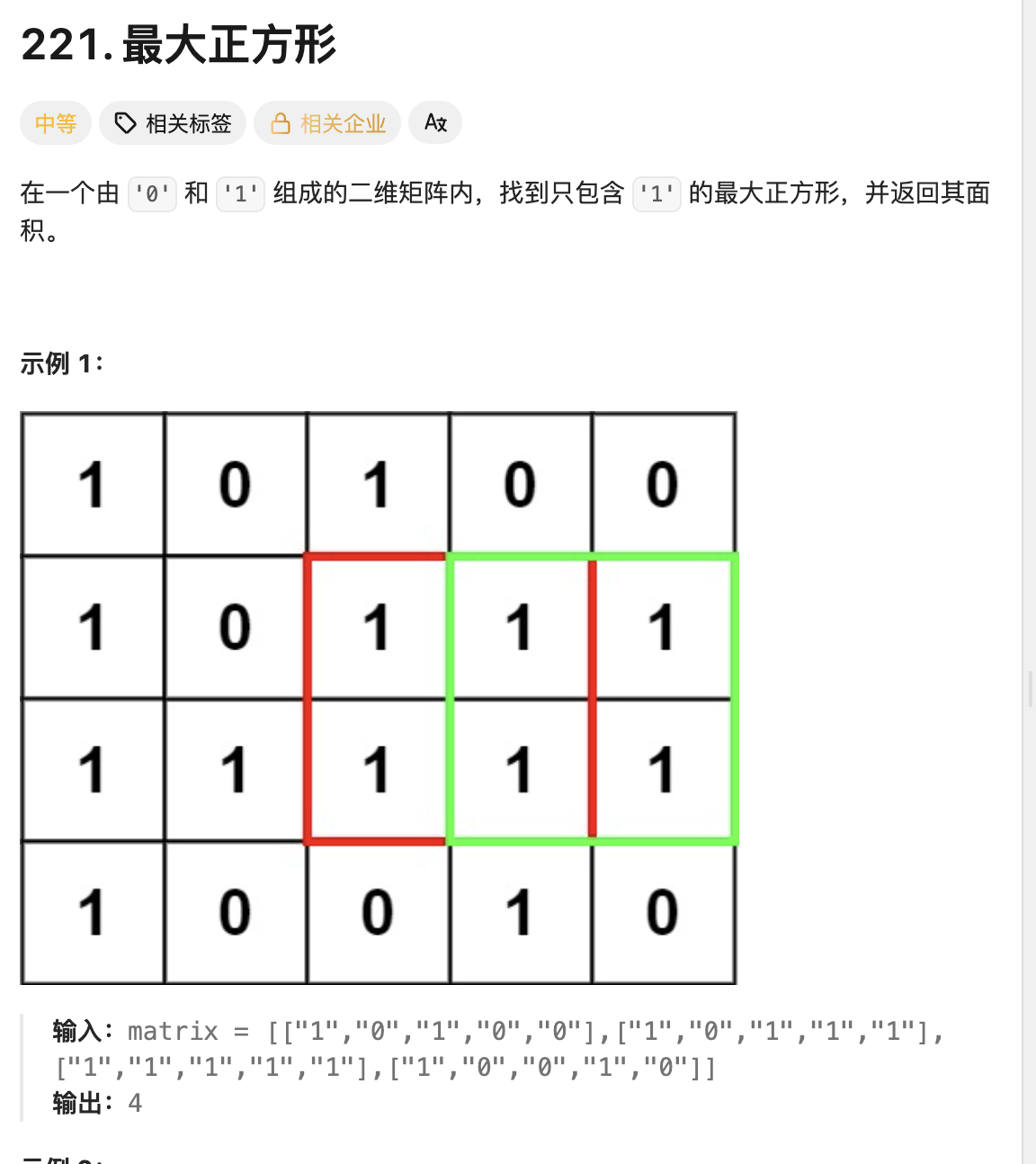
1.题目描述

2.思路

**dp[i][j] 表示：以 (i,j) 为右下角的、全是 ‘1’ 的最大正方形的“边长”。**要把它做大，必须依赖左、上、左上三个位置：dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]。
当 i0 或 j0（第一行或第一列）时，缺少上/左/左上这些邻居，无法扩成更大的正方形；如果此格是 ‘1’，那它能形成的最大正方形就只有自己这个 1×1，所以 dp[i][j] = 1；如果此格是 ‘0’，当然 dp[i][j] = 0。

matrix (3×4):
1 1 1 0
1 1 1 1
0 1 1 1

第一行 i=0：

(0,0)=‘1’ → dp[0][0]=1

(0,1)=‘1’ → dp[0][1]=1

(0,2)=‘1’ → dp[0][2]=1
这些都在第一行，所以只能是 1×1。

到 (1,2) 时就可以用三邻居扩张：

dp[1][2] = 1 + min(dp[0][2], dp[1][1], dp[0][1]) = 1 + min(1,1,1) = 2

3.代码实现

class Solution {public int maximalSquare(char[][] matrix) {//行数int m=matrix.length;//列数int n=matrix[0].length;//定义dp数组int[][] dp=new int[m][n];int side=0;//如果只有矩阵为空，面积直接是0//matrix.length == 0：没有任何行（0×N 矩阵），只有一列，是长方形不满足题意//matrix[0].length == 0：虽然有行，但第一行列数为 0（N×0 矩阵）。长方形不满足题意if(matrix==null||matrix.length==0||matrix[0].length==0){return 0;}//初始化正方形, 先遍历行,再遍历列for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(matrix[i][j]=='1'){ //边界情况//i==0说明只有一行，然后元素又含有1，此时最大的正方形只能有1个，面积为1//j==0说明只有一列，然后元素又含有1，此时最大的正方形只能有1个,面积为1if(i==0||j==0){//当前这个格子位于第一行或第一列。dp[i][j]=1;}else//正常情况{//dp[i][j]本身是正方形，面积为1，要判断它的左、上、左上的元素的值dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;}side=Math.max(side,dp[i][j]);}}}int sum=side*side;return sum;}
}