当前位置：首页 > news >正文

禁止显示网站目录人工做流量的网站

news 2025/10/16 1:11:52

禁止显示网站目录,人工做流量的网站,怎么知道网站哪家公司做的,视频类网站备案1. 引言在现代控制理论中，如何在系统存在噪声和不确定性的情况下实现稳定控制，是工程界普遍面临的问题。经典的 LQR（线性二次型调节器） 能为确定性系统提供最优状态反馈控制，但在状态无法完全观测、传感器存在测量噪声…

1. 引言

在现代控制理论中，如何在系统存在噪声和不确定性的情况下实现稳定控制，是工程界普遍面临的问题。经典的 LQR（线性二次型调节器） 能为确定性系统提供最优状态反馈控制，但在状态无法完全观测、传感器存在测量噪声时，单纯依赖 LQR 便难以保证性能。
此时，LQG（Linear Quadratic Gaussian）控制器应运而生，它将 LQR 控制器 与 卡尔曼滤波器结合，能够在噪声环境中实现对系统的高精度最优控制。

2. LQG 控制的基本思想

LQG 控制的框架非常清晰：

LQR 部分：解决“给定状态下，如何施加控制输入最优”的问题。
卡尔曼滤波部分：解决“如何从带噪测量中恢复真实状态”的问题。

最终，LQG 控制器的作用就是：

在噪声存在时，依然能通过状态估计 + 最优控制，实现系统稳定、能耗平衡的控制效果。

3. 系统建模

考虑一个典型的离散线性系统：

4. LQR 控制器

LQR（Linear Quadratic Regulator，线性二次型调节器） 是现代控制理论中最经典的 最优控制方法 之一。它的目标是：

在满足系统动力学约束的前提下，找到一个最优反馈控制律，使得系统稳定的同时，兼顾控制性能和能量消耗。

换句话说，LQR 不仅追求“误差要小”，还希望“控制输入不要太激烈”，在精度与能耗之间找到最佳平衡点。

LQR 的目标是在状态反馈下找到一个控制律：

调参含义：

增大 Q：系统更重视精度（快速回到目标）
增大 R：系统更重视能耗（减少控制动作）

5. 卡尔曼滤波器

尔曼滤波（Kalman Filter, KF） 是一种在噪声环境下对动态系统状态进行最优估计的算法。

它的目标是：

在系统模型和测量值都不完美的情况下，融合二者的信息，得到最接近真实状态的估计值，并且在均方误差意义下最优。

换句话说，卡尔曼滤波器就是一个智能加权平均器：既不完全相信预测，也不完全相信测量，而是动态决定该信谁更多。

在实际中，xk不可直接获得，只能通过测量 yk 间接获取。

卡尔曼滤波每个时刻分 预测（Prediction） 和 更新（Correction） 两个阶段：

1. 预测（Prediction）：

根据系统模型，预测下一时刻状态及误差：

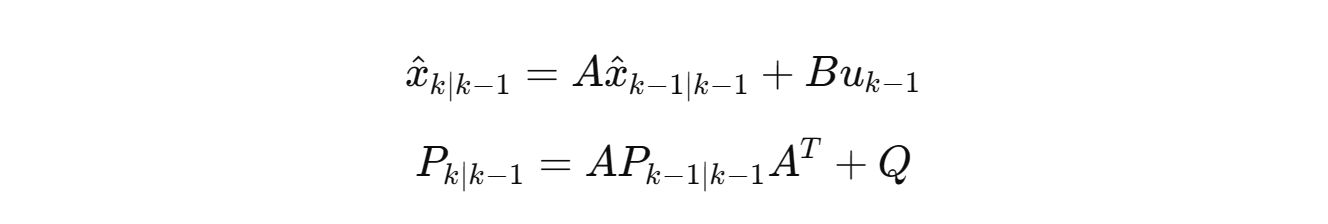
2. 更新（Correction）：

利用测量值来修正预测：

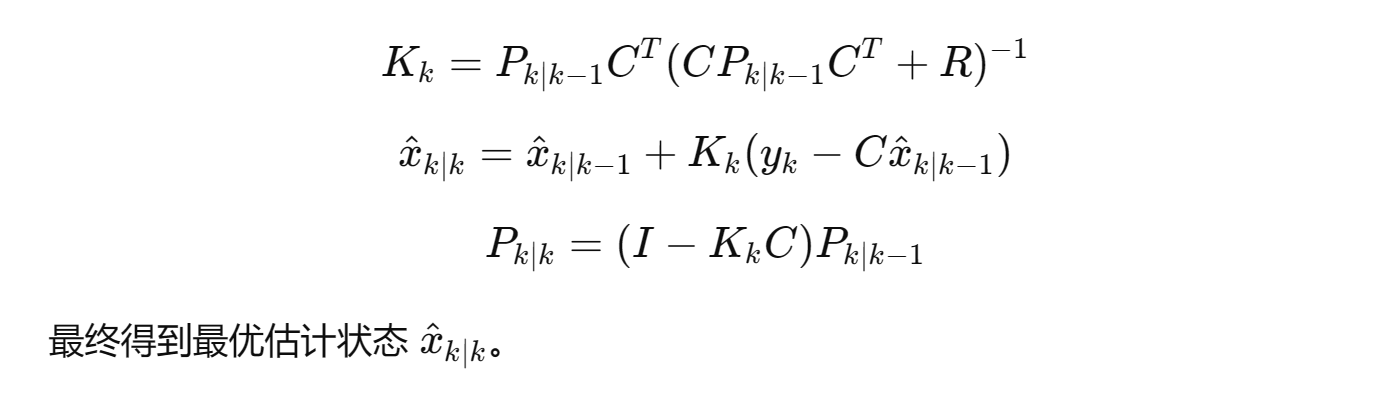
6. LQG 控制器结构

LQG 控制器就是 卡尔曼滤波 + LQR 的组合：

卡尔曼滤波器提供状态估计x^k
LQR 根据估计状态计算控制输入：

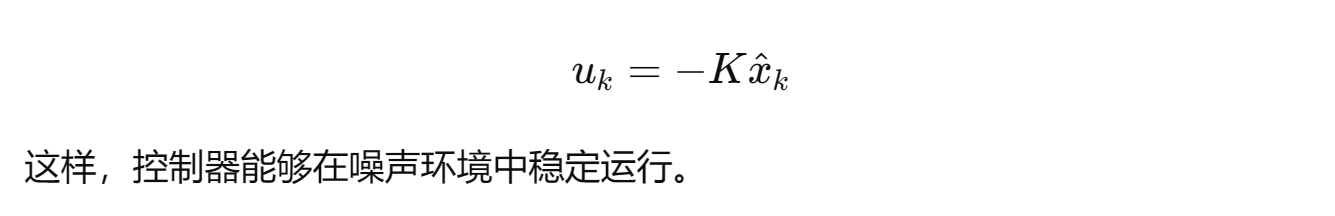
7. Python 实现示例

下面给出一个基于 Python 的简单 LQG 控制实现框架（双积分小车模型）：

import numpy as np
import scipy.linalg# 系统模型
A = np.array([[1, 0, 1, 0],[0, 1, 0, 1],[0, 0, 1, 0],[0, 0, 0, 1]])
B = np.array([[0, 0],[0, 0],[1, 0],[0, 1]])
C = np.eye(4)# 噪声协方差
Q = 0.01 * np.eye(4)   # 过程噪声
R = 0.05 * np.eye(4)   # 测量噪声# LQR 设计
Qx = np.diag([10, 10, 1, 1])
Ru = np.eye(2)
P = scipy.linalg.solve_discrete_are(A, B, Qx, Ru)
K = np.linalg.inv(B.T @ P @ B + Ru) @ (B.T @ P @ A)# 初始值
x_hat = np.zeros((4,1))
P_cov = np.eye(4)def kalman_filter(y, u, x_hat, P_cov):# 预测x_pred = A @ x_hat + B @ uP_pred = A @ P_cov @ A.T + Q# 更新K_gain = P_pred @ C.T @ np.linalg.inv(C @ P_pred @ C.T + R)x_hat = x_pred + K_gain @ (y - C @ x_pred)P_cov = (np.eye(4) - K_gain @ C) @ P_predreturn x_hat, P_cov# 控制器循环
x = np.array([[0],[0],[0],[0]])  # 真值
for k in range(50):# 假设有测量值y = C @ x + np.random.multivariate_normal([0,0,0,0], R).reshape(-1,1)# 控制输入u = -K @ x_hat# 更新状态x = A @ x + B @ u + np.random.multivariate_normal([0,0,0,0], Q).reshape(-1,1)# 卡尔曼滤波更新x_hat, P_cov = kalman_filter(y, u, x_hat, P_cov)