【高中小蓝本】数论 02 最大公约数 最小公倍数
一、求最大公约数的方法
数论中最大公约数的概念。首先说明,当a、b不全为零时,能同时整除a和b的整数(像这类)就是它们的公约数。因为a、b不全为零,根据相关性质,可知a、b的公约数数量是有限的。然后,把这些公约数里最大的那个叫做a、b的最大公约数,用符号
来表示,并且最大公约数是正整数。
1. 辗转相除法(欧几里得算法)
核心逻辑:用较大数除以较小数取余数,再用除数和余数重复此操作,直到余数为0,此时的除数就是最大公约数。公表达:c(x表示a除以b的余数)。

2. 更相减损法(辗转相减法,出自《九章算术》)
步骤:① 若两数都是偶数,用2约简 (就是除以2,重复此步骤直到至少一个数为奇数);
② 用大数减小数,再用所得的 “差” 与 “较小数” 重复相减,直到两数相等(此时的数称为 “等数”);
③ 最终最大公约数为 “等数” 与①中约简的所有2的乘积。
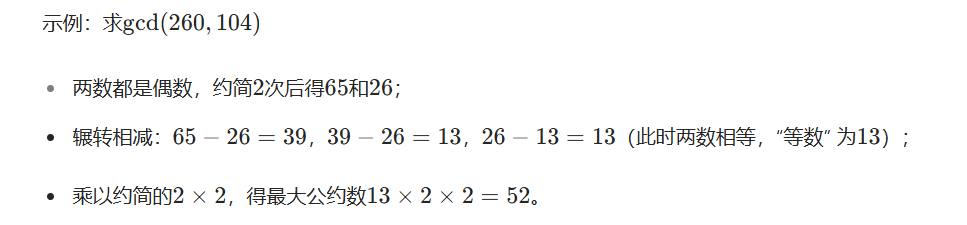
3. 分解质因数法
步骤:将两个数分别分解为质因数的乘积,提取所有公有质因数并相乘,结果即为最大公约数。

4.穷举法
穷举法的基本思路
穷举法(枚举法)求最大公约数的步骤是:
- 找到两个数中 较小的那个数(因为最大公约数不可能大于较小的数)。
- 从这个较小的数开始,向下依次尝试更小的整数。
- 检查每个数是否能同时整除原来的两个数。
- 找到的第一个符合条件的数,就是最大公约数。
性质
结合律
GCD 具有结合律:GCD(a,b,c) = GCD(GCD(a,b), c)
示例:求 gcd (12, 18)
- 较小的数是 12。
- 我们从 12 开始检查:
- 检查 12:
- 12 ÷ 12 = 1(整除)
- 18 ÷ 12 = 1 …… 余 6(不能整除)
- 所以 12 不是最大公约数。
- 检查 12:
- 接下来,按穷举法的规则,我们要检查比 12 小的下一个整数,也就是 11、10、9、8、7、6……
- 11:12 ÷ 11 余 1(不行)
- 10:12 ÷ 10 余 2(不行)
- 9:12 ÷ 9 余 3(不行)
- 8:12 ÷ 8 余 4(不行)
- 7:12 ÷ 7 余 5(不行)
- 6:
- 12 ÷ 6 = 2(整除)
- 18 ÷ 6 = 3(整除)
- 所以 6 是最大公约数。
为什么可以直接跳到 6
虽然穷举法是 “从大到小逐个试”,但在实际操作中,我们知道最大公约数一定是两数之差的约数(这个是数论性质)。
- 18 - 12 = 6
- 所以最大公约数一定是 6 的约数,也就是可能是 6、3、2、1。
- 这样我们可以直接从 6 开始试,减少中间多余的步骤。
✅ 总结第二次判断 6 是因为:
- 穷举法是从较小数开始,由大到小检查。
- 12 不行,就尝试更小的数。
- 利用数学性质可以直接跳到 6(两数之差),减少多余计算。
- 6 正好能同时整除 12 和 18,所以它就是最大公约数。
5. 递归法(基于辗转相除法的递归实现)
通过递归函数实现辗转相除法的逻辑:当余数\(b = 0\)时,返回当前的除数a;否则递归调用\gcd(b, a mod b)。代码逻辑示例(伪代码):
plaintext
int gcd(int a, int b) {if (b == 0) return a;return gcd(b, a % b);
}
示例:求gcd(6, 12),递归过程为gcd(6, 12) to gcd(12, 6) to gcd(6, 0),返回6。
6. 短除法
步骤:用两数的公约数连续去除两数,直到商为互质数(即只有公约数1),最后将所有除数相乘,结果就是最大公约数。
示例:求gcd(36, 54)
先除以公约数 2 得到 18 ,27
再除以公约数3,得到6 ,9
再除以3 得到 2,3 , 2,3 互为质数 。
除数相乘 2*3*3 =18 最大公约数为18。
二、求两个数最小公倍数
求两个数的最小公倍数有多种方法,以下是常用且清晰的方法总结(含原理、步骤与示例):
性质 结合律
多个数的 LCM 同样具有结合律:LCM(a,b,c) = LCM(LCM(a,b), c)。注意:两个数的 LCM 公式为 LCM(a,b) = a×b // GCD(a,b)(先乘后除,避免精度问题)。
一、公式法(利用最大公约数)
核心原理:两个正整数的乘积等于它们的 ** 最大公约数(GCD)与最小公倍数(LCM)** 的乘积,即:
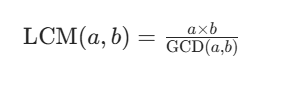
步骤:
- 先求两数的最大公约数(可通过辗转相除法、更相减损法等实现);
- 用两数的乘积除以最大公约数,结果即为最小公倍数。
示例:求LCM(12,18)
- 第一步:求GCD(12,18)。用辗转相除法:18/12 余 6;12 / 6 = 2 余 0,故GCD(12, 18) = 6。
- 第二步:计算最小公倍数:LCM(12, 18) = (12*18)/6=36。
二、分解质因数法
核心原理:将两个数分解为质因数的乘积,取每个质因数的最高次幂相乘,结果即为最小公倍数。
步骤:
- 分别分解两个数的质因数;
- 找出所有质因数,并确定每个质因数在两个数中的最高次幂;
- 将这些最高次幂的质因数相乘。
示例:求
- 分解质因数:12 =2^2*3,18=3^2 * 2;
- 取最高次幂:质因数 2 的最高次幂为 2^2(来自 12),质因数 3 的最高次幂为 3^2(来自 18);
- 相乘:2^2 * 3^2 =36。
三、短除法
核心原理:用两个数的公有质因数连续除,直到商为互质数(只有公约数 1),再将所有除数和最终的商相乘。
步骤:
- 用两数的最小公有质因数(通常从最小的质数开始,如 2、3 等)去除两数,得到商;
- 继续用新商的公有质因数去除,直到商互质;
- 把所有除数和最后两个互质的商相乘。
示例:求 \(\text{LCM}(16, 24)\)
- 用 2 除:\(16 \div 2 = 8\),\(24 \div 2 = 12\);
- 再用 2 除:\(8 \div 2 = 4\),\(12 \div 2 = 6\);
- 再用 2 除:\(4 \div 2 = 2\),\(6 \div 2 = 3\)(此时 2 和 3 互质);
- 相乘:\(2 \times 2 \times 2 \times 2 \times 3 = 48\)。
四、特殊情况快速法
根据两数的关系,可直接得出最小公倍数:
1. 互质关系
若两数的最大公约数为 1(互质),则最小公倍数为两数的乘积。
示例:
- 7 和 8 互质(只有公约数 1),故 \(\text{LCM}(7, 8) = 7 \times 8 = 56\);
- 2、3、5 两两互质,故 \(\text{LCM}(2, 3, 5) = 2 \times 3 \times 5 = 30\)。
2. 倍数关系
若一个数是另一个数的倍数,则较大的数就是最小公倍数。
示例:
- 25 是 5 的倍数,故 \(\text{LCM}(25, 5) = 25\)。
五、累加法(迭乘法)
核心原理:最小公倍数是两数的共同倍数,因此将其中一个数依次扩大倍数,直到能被另一个数整除。
步骤:
- 选两数中较大的数(或任选其一);
- 依次将其扩大 1 倍、2 倍、3 倍……;
- 第一个能被另一个数整除的数,即为最小公倍数。
示例:求 \(\text{LCM}(12, 8)\)
- 选 12,依次扩大:\(12 \times 1 = 12\)(\(12 \div 8\) 余 4,不行);\(12 \times 2 = 24\)(\(24 \div 8 = 3\),能整除);
- 故 \(\text{LCM}(12, 8) = 24\)。
六、枚举法(暴力枚举)
核心原理:从两数的较大值开始,依次加 1,直到找到能同时被两数整除的最小数。
步骤:
- 找出两数中的较大值;
- 从该值开始,依次加 1,检查是否能同时被两数整除;
- 第一个符合条件的数即为最小公倍数。
示例:求 \(\text{LCM}(12, 8)\)
- 较大值为 12;
- 检查 12:\(12 \div 8\) 余 4(不行);
- 检查 13:\(13 \div 12\) 余 1,\(13 \div 8\) 余 5(不行);
- …… 直到 24:\(24 \div 12 = 2\),\(24 \div 8 = 3\)(能整除);
- 故 \(\text{LCM}(12, 8) = 24\)。(注:此方法效率低,适合小数。)
方法适用场景总结
- 公式法、分解质因数法:适合大多数情况,逻辑清晰且计算高效;
- 短除法:直观易操作,适合初学者理解 “质因数与公倍数的关系”;
- 特殊情况快速法:可大幅简化计算(如互质、倍数关系的数);
- 累加法、枚举法:更偏向基础理解或验证,适合小数值或教学演示。
算法题
3334. 数组的最大因子得分 - 力扣(LeetCode)
