当前位置：首页 > news >正文

分治：最大子段和

news 2025/10/15 9:21:47

题目：P1115 最大子段和 - 洛谷

计算左半边的最大子段和，计算右半边的最大子段和，计算中间的最大子段和，返回这三个中最大的。结束条件是 l >= r 时，返回数组所在的这个数。

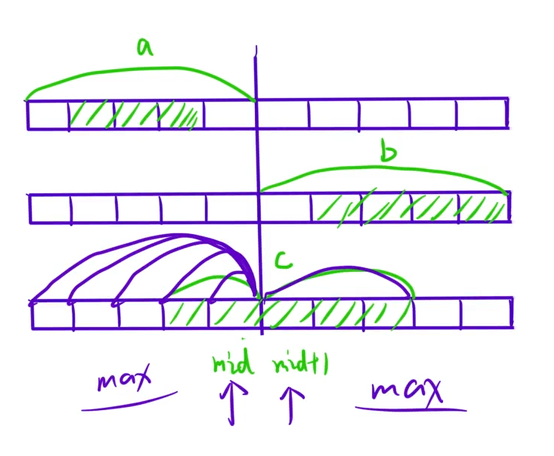
提几个细节问题

分割区间：

将区间分割为 [l, mid-1]和 [mid, r]，这会导致区间重叠或间隙。例如，当 l和 r相邻时，mid-1可能小于 l，导致空区间或无效访问。

正确的分割方式应该是将区间分为 [l, mid]和 [mid+1, r]，确保区间连续且不重叠。

计算跨越中间的最大子段和：

跨越中点的子段应该由左半部分的最大后缀和右半部分的最大前缀和组成。

从中点 mid向左扫描求最大后缀和（从大往左走）从中点 mid+1向右扫描求最大前缀和（从小往右），然后相加。

ret 应该作为局部区间

ret不能作为全局，不然值容易被覆盖出现问题。

循环i的起始点

一个值计算总和，一个值计算最大。有suml, maxl 等于a[mid]（往左走的起点），有sumr，maxr等于a[mid+1]。所以循环i的起点分别是mid-1 ，mid+2。

#include <iostream>
using namespace std;const int N = 2e5 +10; int n;
int a[N];int dfs(int l, int r)
{if (l >= r) return a[l];int mid = (l+r)>>1;int ret = max(dfs(l, mid), dfs(mid+1, r));int suml = a[mid], sumr = a[mid+1];int maxl = suml, maxr = sumr;for (int i = mid-1; i >= l; i--){suml += a[i];maxl = max(maxl, suml);	}	 for (int i = mid+2; i <= r; i++){sumr += a[i];maxr = max(maxr, sumr);}return max(maxr + maxl, ret);
}int main()
{cin >> n;for (int i = 1; i <= n; i++) cin>> a[i];cout << dfs(1, n) << endl;return 0;}