当前位置：首页 > news >正文

CSP-S模拟赛五总结（实际难度远低于提高组）

news 2025/10/15 9:13:45

T1

题面：

第一题一开始没看到是最短路径，然后硬控了我一小时（呜呜呜，下次一定仔细审题）。

因为是最短路径，所以上来肯定直接跑 Dijkstra。那这时有一种非常水的情况：如果从起点到终点的最短路径小于等于 K，那任意两个点都可以连边，直接输出 $\frac{n(n-1)}{2}$ （但如果不判这种情况的话会 WA 一个点）。

另一种情况，就是最短路径比 K 大。这时我们就必须选两个点连起来，使得最短路径更短（当然，不一定是在最短路径上修改），我们假设从起点 $s$ 走了 $i$ 个单位长度，从终点 $t$ 走了 $j$ 个单位长度，那么要满足条件的话就要保证 $i+j+L\le K$ ，也就是 $j\le K-L-i$ ，那 $j$ 能取的上限就是 $K - L - i$ ，因此在这个范围以内的我们都可以取，怎么算有多少个呢？很简单：排个序再二分一下不就对了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
#define INF 0x3f3f3f3f3f3f3f3f
code by plh;
int n,m,s,t,L,K,ans,dis1[200006],dis2[200006],vis[200006];
vector<pair<int,int>>v[200006];
void dijkstra(int st,int *dis)
{priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;for(int i=1;i<=n;i++){dis[i]=INF;vis[i]=0;}dis[st]=0;pq.push(make_pair(dis[st],st));while(!pq.empty()){pair<int,int>p=pq.top();pq.pop();int u=p.second;if(vis[u]){continue;}vis[u]=1;for(auto i:v[u]){if(dis[i.first]>dis[u]+i.second){dis[i.first]=dis[u]+i.second;pq.push(make_pair(dis[i.first],i.first));}}}
}
signed main()
{// freopen("portal.in","r",stdin);// freopen("portal.out","w",stdout);cin>>n>>m>>s>>t>>L>>K;for(int i=1,x,y,z;i<=m;i++){cin>>x>>y>>z;v[x].push_back(make_pair(y,z));v[y].push_back(make_pair(x,z));}dijkstra(s,dis1);if(dis1[t]<=K){cout<<n*(n-1)/2;return 0;}dijkstra(t,dis2);sort(dis1+1,dis1+1+n);sort(dis2+1,dis2+1+n);K-=L;for(int i=1;i<=n;i++){if(K<dis1[i]){break;}int cnt=upper_bound(dis2+1,dis2+n+1,K-dis1[i])-dis2-1;ans+=cnt;}cout<<ans;return 0;
}

T2

题面：

这题让我想到了这道题，只不过比那道题似乎还要好写一点。

首先看到后缀表达式，明显用栈建树，接下来就是要考虑反转表达式的值了。

首先，有两种无可奈何的情况（即必须把值改了）：

$1\mid x=1$ 。
$0\&x=0$ 。

在这两种情况下，你需要把所有决定了表达式的值全部倒过来，这时没办法的。

不过也有其他的：

$0\mid0=0$ 。
$1\&1=1$ 。

这时，左右两边随便选一个变化一下就行，这里也没什么特殊的做法，直接左右子树暴力就行了。

然后就 AC 了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct Tree{int ls,rs,op,num,siz;
}nd[500006];
int t,n,m,ans,a[500006];
string s;
void build()
{stack<int>st;int len=s.size();int num=n;for(int i=0;i<len;i++){if(s[i]=='x'){i++;int z=0;while(s[i]>='0'&&s[i]<='9'){z=z*10+s[i]-'0';i++;}st.push(z);nd[z].siz=1;}else if(s[i]=='&'){int x=st.top();st.pop();int y=st.top();st.pop();num++;nd[num].ls=x,nd[num].rs=y,nd[num].op=1,nd[num].siz=nd[x].siz+nd[y].siz;st.push(num);}else if(s[i]=='|'){int x=st.top();st.pop();int y=st.top();st.pop();num++;nd[num].ls=x,nd[num].rs=y,nd[num].op=2,nd[num].siz=nd[x].siz+nd[y].siz;st.push(num);}}m=num;
}
void dfs(int x)
{if(x<=n){nd[x].num=a[x];return;}if(nd[x].op==1){dfs(nd[x].ls);dfs(nd[x].rs);nd[x].num=(nd[nd[x].ls].num&nd[nd[x].rs].num);}else{dfs(nd[x].ls);dfs(nd[x].rs);nd[x].num=(nd[nd[x].ls].num|nd[nd[x].rs].num);}
}
int dfs1(int x)
{if(x<=n){return 1;}if(nd[x].op==1){if(nd[x].num==1){return min(dfs1(nd[x].ls),dfs1(nd[x].rs));}else{int sum=0;if(nd[nd[x].ls].num==0){sum+=dfs1(nd[x].ls);}if(nd[nd[x].rs].num==0){sum+=dfs1(nd[x].rs);}return sum;}}else if(nd[x].op==2){if(nd[x].num==0){return min(dfs1(nd[x].ls),dfs1(nd[x].rs));}else{int sum=0;if(nd[nd[x].ls].num==1){sum+=dfs1(nd[x].ls);}if(nd[nd[x].rs].num==1){sum+=dfs1(nd[x].rs);}return sum;}}
}
signed main()
{// freopen("logic.in","r",stdin);// freopen("logic.out","w",stdout);cin>>t;while(t--){cin>>n;getline(cin,s);getline(cin,s);for(int i=1;i<=n;i++){cin>>a[i];}build();dfs(m);cout<<dfs1(m)<<'\n';ans=0;for(int i=1;i<=m;i++){nd[i].ls=nd[i].num=nd[i].op=nd[i].rs=nd[i].siz=0;}}return 0;
}

T3

题面：

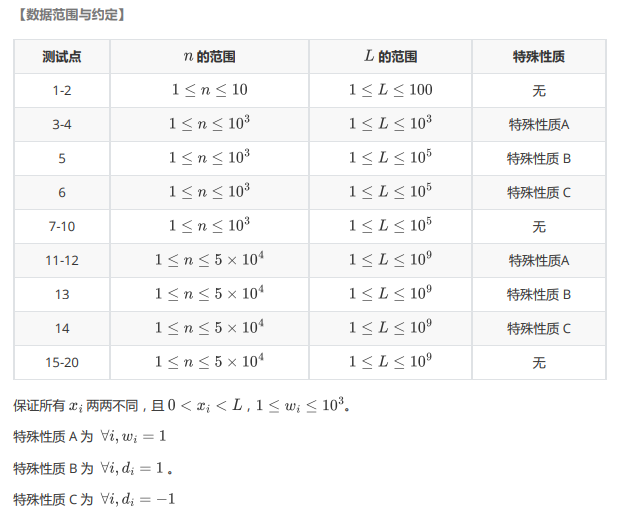
这里有三条重要的性质，如果想不到这题就做不出来（一下所有性质针对的都是在蚂蚁还没进洞之前的情况）：

任意两只蚂蚁的相对移动范围是不会变的（即在最左边的蚂蚁一直在最左边，在中间的蚂蚁一直在中间）。
如果有一只蚂蚁在 $x$ 处，那在 $T$ 时刻过后必然有一只蚂蚁在 $a + T$ 处。
两只蚂蚁相撞，其实就是两只蚂蚁互换了体重且方向不变（这一条最重要！！！）。

其中，前两条性质都可以通过第三条性质证出来（关于我考试时没意识到第三条性质反而用大脑直接想出了前两条性质……然后我没做出来）。

现在有了这三条性质，我们就能很轻松的解决这道题了。首先第一条性质告诉我们：每次回蚁穴的都必定是最边上的蚂蚁，因此在最边上的蚂蚁回去之前，中间的蚂蚁我们是不能让它们“莫名其妙地回去”的。其次第二条性质告诉我们：如果一只蚂蚁所在的位置是 $a$ ，方向向右，那么它所需要的时间就是 $L - a$ ，向左就是 $a$ 。然后结合第一条性质，我们就可以直接算出时间，然后从小到大排序（因为最边上的肯定最小）。

最后根据最后一条性质，我们可以推算出蚂蚁之间体重交换的规律：因为一只蚂蚁经过了很多只蚂蚁之后，最后带走的是最后一只蚂蚁的重量，所以每只蚂蚁在穿过“蚁群”之后的重量都是当前最后一只蚂蚁的重量。而它的重量则给了第一只蚂蚁，第一只蚂蚁的重量给了它之后它又给了第二只蚂蚁……以此类推，最后整个“蚁群”的重量就是：w[0],w[1],w[2],...,w[n-1] w[n]，其中 w[0] 表示穿过“蚁群”的那只蚂蚁重量。

然后我们就可以这样做这道题了：首先算出每只蚂蚁到达蚁穴时的重量和时间，然后按照时间从小到大排序，再从前往后依次扫一遍，如果到了某个位置之后蚁穴内的重量达到了最大限制，那么记录下时间，跳出，最后根据时间算每只蚂蚁能走的最远地点（这里我为了方便，用了相对运动，具体见代码），然后再加上个单调队列，就没了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct Ant{int w,x,d;
}a[50006];
int n,L,sum,ans;
vector<pair<int,int>>v;
int read()
{int z=0,f=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}while(c>='0'&&c<='9'){z=z*10+c-'0';c=getchar();}return z*f;
}
signed main()
{n=read(),L=read();for(int i=1;i<=n;i++){a[i].w=read(),a[i].x=read(),a[i].d=read();sum+=a[i].w;}sort(a+1,a+n+1,[&](Ant x,Ant y){return x.x<y.x;});deque<int>dq;for(int i=n;i>=1;i--){dq.push_front(a[i].w);if(a[i].d==1){v.push_back(make_pair(L-a[i].x,dq.back()));dq.pop_back();}}dq.clear();for(int i=1;i<=n;i++){dq.push_front(a[i].w);if(a[i].d==-1){v.push_back(make_pair(a[i].x,dq.back()));dq.pop_back();}}sort(v.begin(),v.end());int ww=0,t=0;for(auto i:v){ww+=i.second;if(ww>=sum/2){t=i.first;break;}}queue<int>q;for(int i=1;i<=n;i++){if(a[i].d==1){q.push(a[i].x);}else{while(q.front()<a[i].x-t*2)//动用相对运动之力{q.pop();}ans+=q.size();}}cout<<ans;return 0;
}

T4

题面：

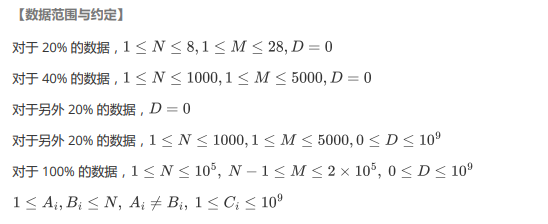
$n - 1$ 条边，还要边权和最小，很容易想到最小生成树。所以上来直接跑一遍 kruskal。

接下来就是换边的问题了：因为我们要在保证边权和最小的情况下让总天数尽可能的少，所以我们要尽可能的换最开始我们用过的边。那要让边权和尽可能的小，我们肯定要尽可能的换边权更大的边，多大呢？直接选最大的边来换。

因此这个问题就变成了这样：我们要从最开始用过的边中选择一条边让边权减掉 D 之后替换最长边（当然最后也必须形成一棵树）。那因为树上边权最大的边一定是 kruskal 算法中的最后一条边，所以我们其实可以先建 $n - 2$ 条边，最后一条边暴力枚举出来，然后就 AC 了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
#define INF 0x3f3f3f3f
code by plh;
struct edge{int st,ed,s,id;
}a[200006];
int n,m,d,fa[100006],b[200006],bb[200006];
int find(int x)
{return fa[x]=(fa[x]==x?fa[x]:find(fa[x]));
}
void merge(int x,int y)
{int fx=find(x);int fy=find(y);fa[fy]=fx;
}
void kruskal()
{for(int i=1;i<=n;i++){fa[i]=i;}sort(a+1,a+m+1,[&](edge x,edge y){return x.s<y.s||x.s==y.s&&b[x.id]<b[y.id];});for(int i=1,cnt=0;i<=m&&cnt<n-2;i++){if(find(a[i].st)!=find(a[i].ed)){bb[a[i].id]=1;merge(a[i].st,a[i].ed);cnt++;}}
}
signed main()
{memset(b,INF,sizeof(b));memset(bb,INF,sizeof(bb));cin>>n>>m>>d;for(int i=1;i<=m;i++){cin>>a[i].st>>a[i].ed>>a[i].s;a[i].id=i;if(i<n){b[i]=1;}}kruskal();int ans=0;for(int i=1;i<=m;i++){a[i].s=max(a[i].s-d,0ll);}sort(a+1,a+m+1,[&](edge x,edge y){return x.s<y.s||x.s==y.s&&b[x.id]<b[y.id];});for(int i=1;i<=m;i++){if(find(a[i].st)==find(a[i].ed)){continue;}merge(a[i].st,a[i].ed);bb[a[i].id]=1;break;}for(int i=1;i<=m;i++){if(b[i]!=bb[i]){ans++;}}cout<<ans/2;return 0;
}