2025年RAS SCI2区，基于事件触发的城市无人机跟踪地面运动目标集成动态任务分配，深度解析+性能实测

---

1.摘要

本文提出了一种通过事件触发机制实现的集成动态任务分配方法，用于多个无人机（UAVs）在城市环境中协同跟踪多个地面移动目标（GMTs）。构建了时变01整数规划（ZOIP）模型用于任务分配，并提出递归视界框架进行路径规划，将问题转化为混合整数非线性规划（MINLP）模型。通过松弛的满意度顺序，设计了一个包含三目标和优先级的模糊满意度目标规划模型，作为集成任务分配中的时变奖励。为了减轻计算负担，设计了基于三种触发条件的事件触发机制，实现集成优化与纯路径规划的切换。考虑到解决集成任务分配MINLP模型的困难，采用了二进制混合粒子群优化（BHPSO）算法进行求解。

2.问题描述

问题假设无人机同构，飞行高度一致；目标状态已知；建筑物高度已知。

无人机模型

四旋翼无人机模型：
$$\{\begin{array}{ll}{\dot{x}}_{ui}=v_i\cos {\psi }_i& \\ {\dot{y}}_{ui}=v_i\sin {\psi }_i& \\ {\dot{z}}_{ui}=0& \\ {\dot{\psi }}_i={\omega }_i& \\ {\dot{v}}_i=-\frac{1}{{\tau }_v}{v}_i+\frac{1}{{\tau }_v}{u}_{vi}& \\ {\dot{\omega }}_i=-\frac{1}{{\tau }_{\omega }}{\omega }_i+\frac{1}{{\tau }_{\omega }}{u}_{\omega i}& \end{array}$$

目标模型

地面目标被视为一个以变化速度移动的理想点，离散模型表示为：
$${\vec{\zeta }}_q(k+1)=G{\vec{\zeta }}_q(k)+e(k)$$

离散模型表示为目标状态的转移方程，包括位置、速度和加速度。状态转移矩阵和过程噪声用于描述目标状态的变化，且无人机具有相同的探测能力。

动态任务分配方法

无人机的任务分配是一个高度复杂的优化问题，需要在任务目标与任务执行相关的多重约束之间取得精细平衡。在实际应用中，将无人机分配给特定目标的标准本质上是动态的，并且取决于与无人机飞行路径相关的时变奖励函数。
max⁡∑i=1N∑q=1Mtiq(k)fiq(k)s.t. ∑i=1Ntiq(k)≥1,∑q=1Mtiq(k)=1tiq(k)∈{0,1}fiq(k)∈Gf(k)i=1,2,…,N;q=1,2,…,M\begin{align*} \max & \sum_{i=1}^{N} \sum_{q=1}^{M} t_{iq}(k) f_{iq}(k) \\ \text{s.t. } & \sum_{i=1}^{N} t_{iq}(k) \geq 1, \quad \sum_{q=1}^{M} t_{iq}(k) = 1 \\ & t_{iq}(k) \in \{0,1\} \\ & f_{iq}(k) \in G_{f}(k) \\ & i = 1,2,\ldots,N; \quad q = 1,2,\ldots,M \end{align*} maxs.t. ​i=1∑N​q=1∑M​tiq​(k)fiq​(k)i=1∑N​tiq​(k)≥1,q=1∑M​tiq​(k)=1tiq​(k)∈{0,1}fiq​(k)∈Gf​(k)i=1,2,…,N;q=1,2,…,M​

奖励函数

为优化未来时间段内的跟踪性能，并最大化总奖励值，本模型引入了滚动时域优化框架。基于模糊目标规划与分布式模型预测控制方法，在预测时域内对三个关键目标进行模糊化。

目标覆盖度奖励

$$f_1^{iq}(k)=\max {\mu }_{{\varsigma }_1^{iq}}(k)=\min \frac{{\varrho }_1^n}{P_{iq}^{\ast }-P_{iq}^{\min }}$$

控制成本奖励

$$f_2^{iq}(k)=\max {\mu }_{{\zeta }_2^{iq}}(k)=\min \frac{{\varrho }_2^p}{\frac{u_v^{\max }+u_w^{\max }}{2}-\frac{u_v^{\ast }+u_w^{\ast }}{2}}$$

传感器能耗奖励

$$f_3^{iq}(k)=\max {\mu }_{{\zeta }_3^{iq}}(k)=\min \frac{{\varrho }_3^n}{{\left(1-D^E\right)}^{-1}}$$

目标函数：
$$\min \frac{1}{3}\left[\frac{{\rho }_1^n}{P_{iq}^{\ast }-P_{iq}^{\min }}+\frac{{\rho }_2^p}{\frac{u_v^{\max }+u_w^{\max }}{2}-\frac{u_v^{\ast }+u_w^{\ast }}{2}}+\frac{{\rho }_3^n}{{\left(1-D^E\right)}^{-1}}\right]+\lambda {\gamma }_{iq}(k)$$

3.二元混合粒子群算法

针对时变混合整数非线性规划这一求解难题，本文采用混合二进制粒子群优化算法（BHPSO）进行求解。在算法设计上，通过混合编码机制分别表示任务匹配关系（二进制变量）和控制输入（连续变量），并采用惩罚函数法将复杂约束条件转化为适应度函数中的惩罚项。当解方案违反避障、防撞、输入限制等关键约束时，惩罚项将自动增加，从而确保算法在追求目标函数最优的同时满足所有操作约束。
$$\begin{array}{rl}{v}_{ad}& =v_{a(d-1)}+c_1\cdot rand()\cdot (p_{ad}-x_{a(d-1)})\\ & +c_2\cdot rand()\cdot (p_{gd}-x_{a(d-1)})\end{array}$$

$$\begin{array}{rl}& \mathrm{or}\\ & \{\begin{array}{ll}s(v_{ad})=\frac{1}{1+\exp (-v_{ad})}& \\ x_{ad}=\{\begin{array}{llc}1& ifrand()\le s(v_{ad})& \\ 0& otherwise& \end{array}& \end{array}\end{array}$$

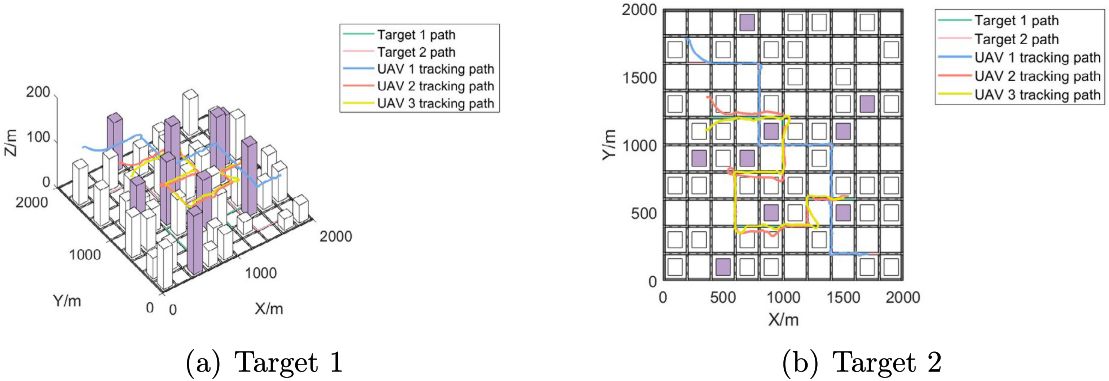
4.结果展示

5.参考文献

[1] Hu C, Li Y, Qu G. Integrated dynamic task allocation via event-triggered for tracking ground moving targets by UAVs in urban[J]. Robotics and Autonomous Systems, 2025: 105061.

6.代码获取

xx

7.算法辅导·应用定制·读者交流

xx