当前位置：首页 > news >正文

十四、OpenCV中的形态学操作

news 2025/10/15 6:57:19

文章目录

- 一、概述
- 二、膨胀（Dilation）的概念
- 三、腐蚀（Erosion）的概念
- 四、开运算（Opening）
- 五、闭运算（Closing）
- 六、形态学梯度（Morphological Gradient）
- 七、顶帽运算（Top-hat）
- 八、黑帽运算（Black-hat）

一、概述

在 OpenCV 中，形态学操作（Morphological Operations）是一类基于图像形状的图像处理方法，常用于去噪、提取轮廓、填补空洞、突出特征等。

二、膨胀（Dilation）的概念

膨胀的作用是：让前景（通常是白色部分）扩大，背景（通常是黑色部分）缩小。

简单理解就是：

图像中的亮区域会“长大”；
暗区域会“被侵蚀”；
小的黑洞会被填平；
分离的小白点可能会被连接起来。

数学定义：
在这里插入图片描述

在 OpenCV 中的实现
函数原型：

void cv::dilate(InputArray src,OutputArray dst,InputArray kernel,Point anchor = Point(-1, -1),int iterations = 1,int borderType = BORDER_CONSTANT,const Scalar& borderValue = morphologyDefaultBorderValue()
);

参数说明：
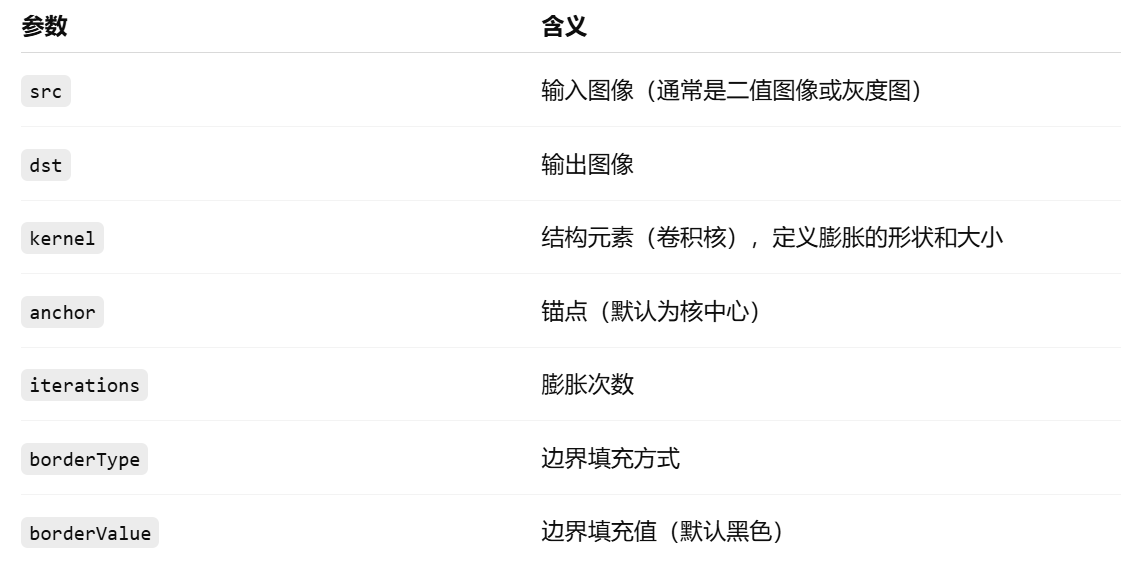
在这里插入图片描述

结构元素的定义
使用 getStructuringElement() 创建核：

Mat kernel = getStructuringElement(MORPH_RECT, Size(5, 5));
// MORPH_RECT：矩形核
// MORPH_ELLIPSE：椭圆形核
// MORPH_CROSS：十字形核

可选类型如下：
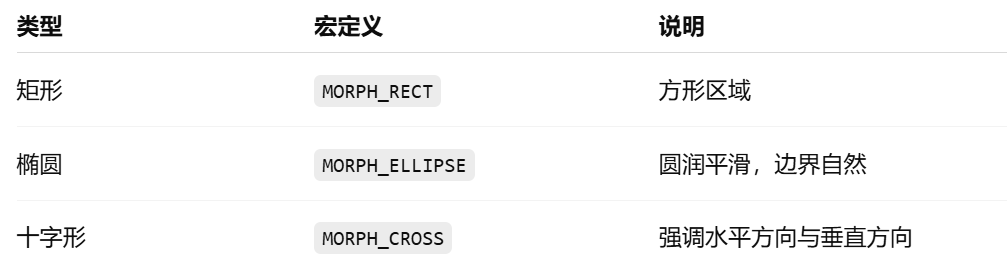
在这里插入图片描述

示例代码：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("binary.png", IMREAD_GRAYSCALE);// 定义结构元素Mat kernel = getStructuringElement(MORPH_RECT, Size(5, 5));// 膨胀操作Mat dst;dilate(src, dst, kernel);imshow("Original", src);imshow("Dilated", dst);waitKey(0);return 0;
}

效果对比
假设原图如下（白色是目标）：

经过膨胀后（3×3核）：

白色区域变大，边缘被“扩张”。

常见应用场景
在这里插入图片描述

在灰度图中的效果
在灰度图像中，膨胀操作的含义变为：每个像素的新值 = 邻域中最大值。

因此可以：

提亮亮区域；
模糊暗边；
用于图像增强。

代码：

dilate(grayImage, result, kernel);

与腐蚀（Erosion）的对比
在这里插入图片描述

三、腐蚀（Erosion）的概念

在图像形态学中，腐蚀（Erosion）是指让图像中的前景（通常是白色部分）区域变小的一种操作。如果把膨胀比作“让白色区域扩张”，那么腐蚀就是“让白色区域收缩”。

直观理解：

膨胀是“白色吃黑色”
腐蚀是“黑色吃白色”。

腐蚀的核心思想是：

用一个结构元素（Kernel）在图像上滑动，
只有当结构元素完全被白色像素覆盖时，输出位置才设为白色，否则为黑色。

在这里插入图片描述

在 OpenCV 中，可以使用以下函数来实现腐蚀：

cv::erode(src, dst, kernel, anchor, iterations, borderType, borderValue);

参数详解：
在这里插入图片描述
结构元素（kernel）可以使用以下方式生成：

cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3));

结构元素类型包括：

MORPH_RECT（矩形）
MORPH_ELLIPSE（椭圆）
ORPH_CROSS（十字形）

示例代码：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("input.png", IMREAD_GRAYSCALE);Mat dst;// 创建3x3矩形结构元素Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));// 腐蚀操作erode(src, dst, kernel);imshow("原图", src);imshow("腐蚀后", dst);waitKey(0);return 0;
}

效果说明：
在这里插入图片描述

四、开运算（Opening）

定义：开运算 = 腐蚀（Erosion） → 膨胀（Dilation）

公式表示为：
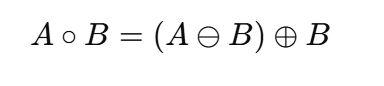
在这里插入图片描述
原理理解：

第一步：腐蚀
去掉目标物体边界上的小白点、小毛刺，分离靠得太近的物体。
第二步：膨胀
让剩下的主体恢复原来的大小。

这样可以：

去除小的噪声点
保留主体形状
分离相邻目标

代码示例：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("binary.png", IMREAD_GRAYSCALE);Mat dst;// 创建结构元素Mat kernel = getStructuringElement(MORPH_RECT, Size(5, 5));// 开运算：先腐蚀后膨胀morphologyEx(src, dst, MORPH_OPEN, kernel);imshow("Original", src);imshow("Open Operation", dst);waitKey(0);return 0;
}

开运算效果举例：
原图（含噪点）：

腐蚀 → 小白点被去除；膨胀 → 主体恢复形状；最终：噪声消除，目标保持。

五、闭运算（Closing）

定义：闭运算 = 膨胀（Dilation） → 腐蚀（Erosion）

公式表示为：
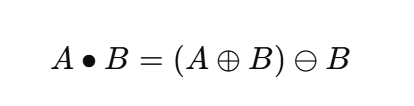
在这里插入图片描述

原理理解：

第一步：膨胀
填补前景区域中的小黑洞、间隙。
第二步：腐蚀
恢复目标边界到原来的大小。

这样可以：

填补小黑洞
连接断裂的目标
保持整体形状

代码示例：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("binary.png", IMREAD_GRAYSCALE);Mat dst;Mat kernel = getStructuringElement(MORPH_RECT, Size(5, 5));// 闭运算：先膨胀后腐蚀morphologyEx(src, dst, MORPH_CLOSE, kernel);imshow("Original", src);imshow("Close Operation", dst);waitKey(0);return 0;
}

开与闭的对比总结
在这里插入图片描述

六、形态学梯度（Morphological Gradient）

定义：梯度 = 膨胀 − 腐蚀

公式为：
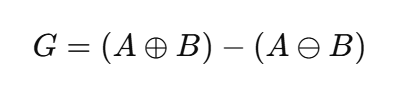
在这里插入图片描述
原理理解：
梯度的本质是提取前景的边缘：

膨胀会让白色区域“变大”；
腐蚀会让白色区域“变小”；
两者相减后，留下的就是边缘区域。

示例代码：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("binary.png", IMREAD_GRAYSCALE);Mat dst;Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));// 形态学梯度 = 膨胀 - 腐蚀morphologyEx(src, dst, MORPH_GRADIENT, kernel);imshow("Original", src);imshow("Morphological Gradient", dst);waitKey(0);return 0;
}

效果：结果类似于边缘检测（类似 Canny 或 Sobel），但基于形态学原理：

对噪声更鲁棒；
特别适用于二值图像或分割掩码的边缘提取。

七、顶帽运算（Top-hat）

定义：顶帽 = 原图 − 开运算结果

公式：
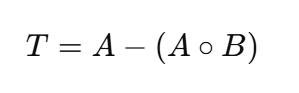
在这里插入图片描述
原理理解：
开运算会“去掉小的亮点”并平滑区域。所以原图减去开运算结果后，留下的就是那些比周围更亮的小目标。

示例代码：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("gray.png", IMREAD_GRAYSCALE);Mat dst;Mat kernel = getStructuringElement(MORPH_RECT, Size(15, 15));// 顶帽运算：原图 - 开运算morphologyEx(src, dst, MORPH_TOPHAT, kernel);imshow("Original", src);imshow("Top-hat", dst);waitKey(0);return 0;
}

八、黑帽运算（Black-hat）

定义：黑帽 = 闭运算结果 − 原图

公式：
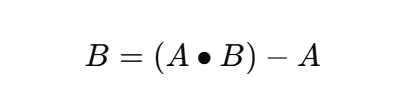
在这里插入图片描述
原理理解：
闭运算会填补小的黑洞、阴影区域；所以闭运算结果减去原图后，得到的就是那些比周围更暗的小区域。

示例代码：

#include <opencv2/opencv.hpp>
using namespace cv;int main() {Mat src = imread("gray.png", IMREAD_GRAYSCALE);Mat dst;Mat kernel = getStructuringElement(MORPH_RECT, Size(15, 15));// 黑帽运算：闭运算 - 原图morphologyEx(src, dst, MORPH_BLACKHAT, kernel);imshow("Original", src);imshow("Black-hat", dst);waitKey(0);return 0;
}