织梦模板大气网站建设类网站模板php做网站主题

数组是最简单的数据结构。数组的一个应用是高精度，高精度算法就是大数的计算方法。

        例如两个整数的计算，C++的最大数据类型是64位的long long，更大的数不能直接计算，需要用数组来模拟。例如两个200位的十进制数相加，定义int a[205]和int b[205]，a[i]和b[i]代表整数的第i位，a[0]为个位，a[1]为十位，以此类推。

一、以下是关于大数组变量分配问题的三点重要知识点:

第一点：

        使用很大的数组时，不要使用malloc()动态分配，因为动态分配需要多写代码而且容易出错。大数组应该定义为全局静态数组，而且不需要初始化为0，因为全局变量在编译时会自动初始化为全0。

代码示例：

#include<bits/stdc++.h>
using namespace std;
int a[10000000];
int main()
{cout<<a[0];return 0;
}

第二点：

        大数组不能定义在函数内部，可能会导致栈溢出错误。因为大多数编译器的局部变量是在用到时才分配，大小不能超过栈，而栈一般大小不会很大。下面代码这样使用很可能会报错：

#include<bits/stdc++.h>
using namespace std;int main()
{int a[10000000]={0};cout<<a[0];return 0;
}

第三点：

        注意全局变量和局部变量的初值。全局变量如果没有赋值，在编译时会被自动初始化为0.在函数内部定义的局部变量，若需要初值为0，一定要初始化为0，否则初值不可预测。

#include<bits/stdc++.h>
using namespace std;int a;
int c=999;
int main()
{int b;cout<<a<<endl;cout<<b<<endl;cout<<c<<endl;return 0;
}

二、高精度计算（加、减、乘、除）

        模拟每一位的计算，并处理进位或者借位。注意数字的读取和存储。设整数a有1000位，因为数值太大，无法直接赋值给变量,所以不能按数字读入，只能按字符读入。可以用字符串string读入大数sa，然后转换为int a[ ]，一个字符 sa[ ]存为一位数字a[ ]。注意存储的顺序,在读入的时候,字符串sa[0]是最高位，sa[n-1]是最低位；但是在计算时习惯用a[0]表示最低位，a[n-1]表示最高位，所以需要把输入的字符串 sa 倒过来存到 a[ ]中。

接下来看加、减、乘、除四种高精度计算来熟悉数组的应用： 

关于开数组大小（以下面高精度加法为例）：

        开数组 a 和 b 的大小为 1005 是一个经验值，主要是为了确保能够处理足够大的整数，同时避免数组越界的问题。以下是具体的依据和原因：

---

1. 输入长度的限制

• 代码中假设输入的两个大整数的长度（位数）不会超过 1000 位。

• 数组大小为 1005，其中 1000 位用于存储输入的数字，额外的 5 位是为了处理可能的进位和边界情况。

---

2. 进位处理

• 在大整数加法中，最高位可能会产生进位。例如：999 + 1 = 1000

  这里，3 位数相加后变成了 4 位数，因此需要额外的一位来存储进位。

• 数组大小为 1005，可以确保即使输入的两个数都是 1000 位，且最高位产生进位，也不会发生数组越界。

---

3. 边界安全性

• 在代码中，数组 a 和 b 的下标是从 0 到 lmax-1，而 lmax 的最大值是 lena 或 lenb 的最大值加 1（如果有进位）。

• 如果输入的两个数都是 1000 位，且最高位有进位，那么 lmax 的最大值为 1001。

• 数组大小为 1005，可以确保即使 lmax 达到 1001，也不会发生数组越界。

---

4. 经验值

• 在实际编程竞赛或算法题中，通常会将数组大小设置为比题目要求的最大输入规模稍大一些，以避免边界问题。

• 1005 是一个常见的经验值，既能满足大多数大整数运算的需求，又不会占用过多的内存。

---

5. 代码中的具体体现

• 在代码中，数组 a 和 b 的大小为 1005，而输入的两个字符串 sa 和 sb 的长度最大为 1000。

• 即使两个 1000 位的数相加，结果最多为 1001 位，因此 1005 的大小足够安全。

---

6. 如果需要处理更大的数

• 如果需要处理更大的整数（例如 10^6 位），可以将数组大小调整为更大的值，例如 a[1000005] 和 b[1000005]。

• 但需要注意，数组大小过大会占用更多的内存，因此需要根据实际需求进行权衡。

---

总结

数组大小设置为 1005 是一个经验值，主要基于以下考虑：

1. 输入的最大长度为 1000 位。

2. 最高位可能产生进位，需要额外的一位。

3. 为了避免数组越界，通常会设置一个比实际需求稍大的值。

        如果题目明确规定了输入的最大长度，可以根据具体需求调整数组大小。例如，如果题目规定输入的最大长度为 10^6，那么可以将数组大小设置为 a[1000005] 和 b[1000005]。

1、高精度加法

P1601 A+B Problem（高精） - 洛谷

算法代码：

#include<bits/stdc++.h>  // 包含常用的头文件，如iostream、string等
using namespace std;char a[1005], b[1005];  // 定义两个字符数组a和b，用于存储两个大整数的每一位数字// 定义函数add，用于实现两个大整数的加法
string add(string sa, string sb)
{int lena = sa.size(), lenb = sb.size();  // 获取两个字符串的长度// 将字符串sa中的字符转换为数字，并逆序存储到数组a中for(int i = 0; i < lena; i++){a[lena - 1 - i] = sa[i] - '0';  // sa[i] - '0'将字符转换为数字}// 将字符串sb中的字符转换为数字，并逆序存储到数组b中for(int i = 0; i < lenb; i++){b[lenb - 1 - i] = sb[i] - '0';  // sb[i] - '0'将字符转换为数字}int lmax = lena > lenb ? lena : lenb;  // 获取两个字符串中较长的长度// 逐位相加，并处理进位for(int i = 0; i < lmax; i++){a[i] += b[i];  // 将a[i]和b[i]相加a[i + 1] += a[i] / 10;  // 处理进位，将进位加到下一位a[i] %= 10;  // 保留当前位的个位数}// 如果最高位有进位，则增加结果的长度if(a[lmax]){lmax++;}string ans;  // 定义字符串ans，用于存储最终的结果// 将数组a中的数字逆序转换为字符串for(int i = lmax - 1; i >= 0; i--){ans += a[i] + '0';  // a[i] + '0'将数字转换为字符}return ans;  // 返回结果字符串
}int main()
{string sa, sb;  // 定义两个字符串sa和sb，用于存储输入的两个大整数cin >> sa >> sb;  // 从标准输入读取两个大整数cout << add(sa, sb);  // 调用add函数进行加法运算，并输出结果return 0;
}

        由于C++中的int类型无法处理非常大的整数，因此这里通过字符串来表示大整数，并模拟手工加法的过程来实现两个大整数的相加。 

代码思路总结

1. 输入处理：从标准输入读取两个大整数，存储为字符串sa和sb。

2. 字符转数字：将字符串中的字符转换为数字，并逆序存储到数组a和b中。逆序存储是为了方便从低位到高位进行加法运算。

3. 逐位相加：从低位到高位逐位相加，并处理进位。如果某一位的和大于等于10，则将进位加到下一位。

4. 处理最高位进位：如果最高位相加后有进位，则增加结果的长度。

5. 结果转换：将数组a中的数字逆序转换为字符串，得到最终的结果。

6. 输出结果：输出相加后的结果。

2、高精度减法 

P2142 高精度减法 - 洛谷 

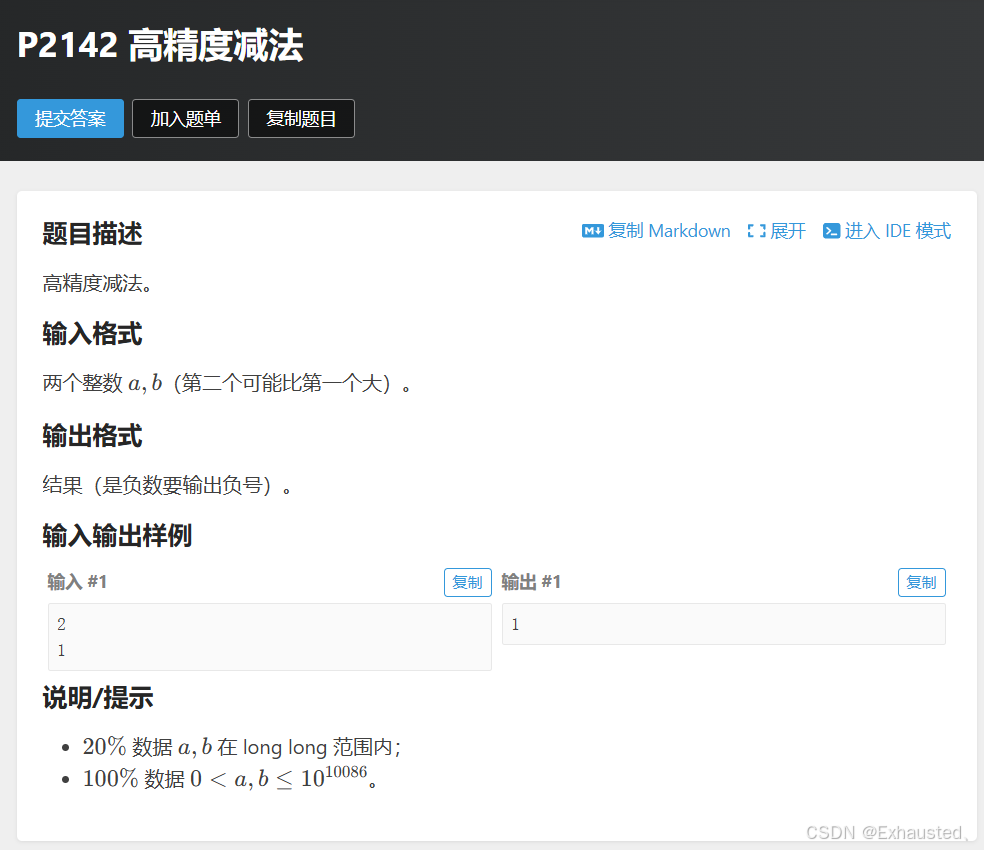
代码思路

        这段代码实现的是大整数减法。由于 C++ 的 int 或 long long 类型无法处理非常大的整数，因此通过字符串来表示大整数，并模拟手工减法的过程来实现两个大整数的相减。

算法代码： 

#include<bits/stdc++.h>  // 包含常用的头文件，如iostream、string等
using namespace std;char a[11000], b[11000];  // 定义两个字符数组a和b，用于存储两个大整数的每一位数字// 定义函数sub，用于实现两个大整数的减法
string sub(string sa, string sb)
{// 如果两个数相等，直接返回 "0"if (sa == sb){return "0";}// 判断结果是否为负数bool neg = 0;if (sa.size() < sb.size() || (sa.size() == sb.size() && sa < sb)){swap(sa, sb);  // 交换sa和sb，确保sa >= sbneg = 1;       // 标记结果为负数}int lena = sa.size(), lenb = sb.size();  // 获取两个字符串的长度// 将字符串sa中的字符转换为数字，并逆序存储到数组a中for (int i = 0; i < lena; i++){a[lena - 1 - i] = sa[i] - '0';  // sa[i] - '0'将字符转换为数字}// 将字符串sb中的字符转换为数字，并逆序存储到数组b中for (int i = 0; i < lenb; i++){b[lenb - 1 - i] = sb[i] - '0';  // sb[i] - '0'将字符转换为数字}int lmax = lena;  // 结果的最大长度初始化为lena// 逐位相减，并处理借位for (int i = 0; i < lmax; i++){a[i] -= b[i];  // 将a[i]和b[i]相减if (a[i] < 0)  // 如果当前位不够减，需要借位{a[i] += 10;  // 借位后当前位加10a[i + 1]--;  // 高位减1}}// 去掉结果的前导零while (!a[--lmax] && lmax > 0);  // 从最高位开始，找到第一个不为0的位置lmax++;  // 调整lmax为有效长度// 将数组a中的数字逆序转换为字符串string ans;for (int i = lmax - 1; i >= 0; i--){ans += a[i] + '0';  // a[i] + '0'将数字转换为字符}// 如果结果为负数，添加负号if (neg){ans = "-" + ans;}return ans;  // 返回结果字符串
}int main()
{string sa, sb;  // 定义两个字符串sa和sb，用于存储输入的两个大整数cin >> sa >> sb;  // 从标准输入读取两个大整数cout << sub(sa, sb);  // 调用sub函数进行减法运算，并输出结果return 0;
}

核心逻辑：

1. 输入处理：从标准输入读取两个大整数，存储为字符串 sa 和 sb。

2. 判断大小：如果 sa < sb，则交换 sa 和 sb，并标记结果为负数。

3. 字符转数字：将字符串中的字符转换为数字，并逆序存储到数组 a 和 b 中（逆序存储是为了方便从低位到高位进行减法运算）。

4. 逐位相减：从低位到高位逐位相减，并处理借位。

5. 去掉前导零：去掉结果中的前导零。

6. 结果转换：将数组 a 中的数字逆序转换为字符串，得到最终的结果。

7. 输出结果：输出相减后的结果。

3、高精度乘法 

P1303 A*B Problem - 洛谷 

        这段代码实现了一个高精度乘法算法，用于计算两个非常大的非负整数的乘积。由于输入的数字可能非常大（不超过 102000102000），因此不能直接使用普通的整数类型来存储和计算。

算法代码：

#include <bits/stdc++.h>  // 包含标准库头文件，提供常用的数据结构和算法
using namespace std;      // 使用标准命名空间int a[2005], b[2005], c[4005];  // 定义数组a和b存储输入的两个大数，c存储乘积结果string mul(string sa, string sb) {  // 定义乘法函数，接受两个字符串形式的大数if(sa == "0" || sb == "0") return "0";  // 如果其中一个数为0，直接返回"0"int lena = sa.size(), lenb = sb.size();  // 获取两个大数的长度// 将字符串sa转换为整数数组a，反转存储，方便从低位到高位计算for(int i = 0; i < lena; i++) a[lena - i] = sa[i] - '0';// 将字符串sb转换为整数数组b，反转存储for(int i = 0; i < lenb; i++) b[lenb - i] = sb[i] - '0';// 模拟竖式乘法，逐位相乘并累加到结果数组c中for(int i = 1; i <= lena; i++)for(int j = 1; j <= lenb; j++)c[i + j - 1] += a[i] * b[j];  // c[i+j-1]存储a[i]和b[j]的乘积// 处理进位，确保每一位的结果都在0到9之间for(int i = 1; i <= lena + lenb; i++) {c[i + 1] += c[i] / 10;  // 将进位加到下一位c[i] %= 10;             // 当前位只保留个位数}string ans;  // 定义字符串ans存储最终结果// 如果最高位有值，将其添加到结果字符串中if(c[lena + lenb]) ans += c[lena + lenb] + '0';// 从高位到低位将结果数组c中的数字转换为字符并添加到ans中for(int i = lena + lenb - 1; i >= 1; i--)ans += c[i] + '0';return ans;  // 返回结果字符串
}int main() {string sa, sb;  // 定义字符串sa和sb存储输入的两个大数cin >> sa >> sb;  // 读取输入cout << mul(sa, sb);  // 调用mul函数计算乘积并输出结果return 0;  // 程序结束
}

 代码思路总结

1. 输入处理：

   • 将输入的两个大数字符串转换为整数数组，并反转存储，方便从低位到高位计算。

2. 乘法计算：

   • 模拟小学竖式乘法，逐位相乘并将结果累加到结果数组 c 中。

3. 进位处理：

   • 处理乘法过程中产生的进位，确保每一位的结果都在0到9之间。

4. 结果输出：

   • 将结果数组 c 转换为字符串并输出。

关键点

• 反转存储：将输入字符串反转存储，方便从低位到高位计算。

• 逐位相乘：通过双重循环逐位相乘并累加结果。

• 进位处理：通过循环处理进位，确保结果的正确性。

• 结果转换：将结果数组转换为字符串并输出。

4、高精度除法 

P1480 A/B Problem - 洛谷

方法一（模拟）： 

        通过模拟竖式除法的方式，实现了大数除以小数的计算。通过逐位计算商和余数，并处理前导零，最终输出商的整数部分。适用于被除数非常大而除数较小的情况。

算法代码：

#include <bits/stdc++.h>  // 包含标准库头文件，提供常用的数据结构和算法
using namespace std;      // 使用标准命名空间long long a[10001], b, c[10001];  // 定义数组a存储被除数，b存储除数，c存储商int main() {string sa;  // 定义字符串sa存储被除数cin >> sa >> b;  // 读取被除数和除数int len = sa.size();  // 获取被除数的长度// 将被除数逐位存储到数组a中for (int i = 1; i <= len; i++)a[i] = sa[i-1] - '0';  // 将字符转换为数字并存储到数组a中long long d = 0;  // 定义变量d存储余数// 逐位计算商和余数for (int i = 1; i <= len; i++) {c[i] = (d * 10 + a[i]) / b;  // 计算当前位的商d = (d * 10 + a[i]) % b;     // 计算新的余数}int lenc = 1;  // 定义变量lenc用于删除前导零// 跳过商的前导零，找到第一个非零数字的位置while (c[lenc] == 0 && lenc < len) lenc++;// 输出商的整数部分for (int i = lenc; i <= len; i++) cout << c[i];return 0;  // 程序结束
}

 逐行注释解释

1. 头文件和命名空间：

   • #include <bits/stdc++.h>：包含标准库头文件，提供常用的数据结构和算法。

   • using namespace std;：使用标准命名空间。

2. 变量定义：

   • long long a[10001], b, c[10001];：定义数组 a 存储被除数的每一位，b 存储除数，c 存储商的每一位。

3. 主函数：

   • int main() {：主函数开始。

4. 输入处理：

   • string sa;：定义字符串 sa 存储被除数。

   • cin >> sa >> b;：读取被除数和除数。

5. 获取被除数长度：

   • int len = sa.size();：获取被除数的长度。

6. 将被除数逐位存储到数组 a 中：

   • for (int i = 1; i <= len; i++) a[i] = sa[i-1] - '0';：将字符转换为数字并存储到数组 a 中。

7. 定义余数变量：

   • long long d = 0;：定义变量 d 存储余数。

8. 逐位计算商和余数：

   • for (int i = 1; i <= len; i++) {：循环逐位计算商和余数。

   • c[i] = (d * 10 + a[i]) / b;：计算当前位的商。

   • d = (d * 10 + a[i]) % b;：计算新的余数。

9. 删除前导零：

   • int lenc = 1;：定义变量 lenc 用于删除前导零。

   • while (c[lenc] == 0 && lenc < len) lenc++;：跳过商的前导零，找到第一个非零数字的位置。

10. 输出商的整数部分：

    • for (int i = lenc; i <= len; i++) cout << c[i];：从第一个非零数字开始输出商的整数部分。

11. 程序结束：

    • return 0;：主函数结束，程序正常退出。

方法二（连续减）：  

#include <bits/stdc++.h>  // 包含标准库头文件
using namespace std;string subtract(string a, string b) {// 实现大数减法，a - bint lenA = a.size(), lenB = b.size();// 补齐位数，方便计算while (lenB < lenA) b = "0" + b;int carry = 0;string result;for (int i = lenA - 1; i >= 0; i--) {int digitA = a[i] - '0';int digitB = b[i] - '0';int diff = digitA - digitB - carry;if (diff < 0) {diff += 10;carry = 1;} else {carry = 0;}result = char(diff + '0') + result;}// 删除前导零result.erase(0, result.find_first_not_of('0'));return result.empty() ? "0" : result;
}string divideBySubtraction(string a, string b) {if (b == "0") return "NaN";  // 除数为0，返回无效值string quotient = "0";  // 初始化商为0while (a.size() > b.size() || (a.size() == b.size() && a >= b)) {a = subtract(a, b);  // a = a - b// 商加1int qLen = quotient.size();int carry = 1;for (int i = qLen - 1; i >= 0; i--) {int digit = quotient[i] - '0' + carry;if (digit >= 10) {digit -= 10;carry = 1;} else {carry = 0;}quotient[i] = digit + '0';}if (carry) quotient = "1" + quotient;}return quotient;  // 返回商
}int main() {string a, b;cin >> a >> b;  // 读取被除数和除数cout << divideBySubtraction(a, b) << endl;  // 输出商return 0;
}

代码思路

1. 大数减法：

   • 实现一个函数 subtract，用于计算两个大数的差。

   • 通过逐位相减并处理借位，得到结果。

2. 除法实现：

   • 使用 subtract 函数，不断从被除数 a 中减去除数 b，直到 a 小于 b。

   • 每次减法操作后，商加1。

   • 最终返回商。

3. 主函数：

   • 读取被除数和除数，调用 divideBySubtraction 函数计算商并输出。

示例

输入：10 3

输出：3

解释：

• 10 连续减去 3，减了 3 次，剩下 1（不够减），所以商是 3。

优缺点

优点：

• 实现简单，逻辑直观。

• 适用于小规模的除法计算。

缺点：

• 效率较低，尤其是当被除数很大而除数很小时，减法次数会非常多。

• 对于非常大的数（如 105000105000），这种方法会非常慢，甚至无法在合理时间内完成计算。

总结

        使用减法实现除法是一种简单直观的方法，适用于小规模的除法计算。但对于大数除法，效率较低，通常需要使用更高效的算法（如竖式除法或高精度除法）。