CSP集训错题集 第五周
B

这题没做出来是真说不过去,想打自己两棒子。
因为密码学里有一些类似的案例,pq素数十分接近,就能通过开根号n来找pq。我知道这题肯定是往 这上面去想,但还是没想清楚。
那么现在马后炮来了:为什么要这么做?有什么好处?
很容易想到,如果你遍历x和y,那是一个规划问题,时间复杂度为 ,所以我们得把
看成一个整体。这样的,我们寻找x,然后计算相应的y方,也就是tmp。
这里的计算是有损失的,准确的函数表达我理解的是 ,那么
,我们目前找出来的tmp是
,如果开根号,它一定是落在[y,y+1]这个区间的。
所以我们找到局部最小值rgans,再和之前的最小值比较,就是最后答案。
写代码时划重点,不能int i=0,必须i64 i=0,因为问题出在中间计算上,tmp=n-i*i,这个i*i会导致整数溢出,结果是未定义行为。
Code
#include<iostream>
#include<cmath>
#define i64 long long
using namespace std;
i64 n=0,tmp=0,ya=0,yb=0;
i64 rgans=1e9+7,ans=1e9+7;
int main() {cin>>n;for(i64 i=0;i<=(i64)sqrt(n);i++){tmp=n-i*i;if(tmp<0) continue;//tmp表示y方ya=(i64)sqrt(tmp);yb=(i64)sqrt(tmp)+1;//cout<<tmp<<' '<<abs(i*i+ya*ya-n)<<' '<<abs(i*i+yb*yb-n)<<endl;rgans=min(abs(i*i+ya*ya-n),abs(i*i+yb*yb-n));ans=min(rgans,ans);}cout<<ans;return 0;
}
C

这是 atcoder_abc331_b 题,我当时以为自己蠢到这题都写不出。
结果一查,居然是dp!
我一直都知道dp这个东西但是从来没主动用过,也不会构造。于是我把攻略的构造方法写在这以加深理解。
首先要理解到,不浪费任何一个鸡蛋,那么一定要是6 8 12三者能相加凑出来的数字,我暂且称为临界点。即使如此也还可能会有浪费,比如你要买12个但是最优解是买2盒8只的。所以这个临界也是相对的。
把其他点设置为最大值mx,这题的解法就是只有临界点有更新的机会,其它点保持mx不动。最后就是算n本身到n+11的最小值,因为你顶多多买一盒12个的,浪费11个。
然后对于6、8、12,他们的关系是平行的,而不会是else if。因为比如对于N=24,有可能3*8比4*6效果更好,但是如果你一直死磕4*6,那么就不会跳转进入3*8这一层。
(解法感觉有点怪怪的,没见过这样的dp,也许是我太菜了吧)
Code
#include<iostream>
#define mx 1e9+7
using namespace std;
long long dp[120]={0};
long long n,s,m,l,ans=mx;
void init();
int main() {cin>>n>>s>>m>>l;init();for(int i=0;i<=n;i++){if(dp[i]==mx) continue;if(i+6<=n+11) dp[i+6]=min(dp[i+6],dp[i]+s);if(i+8<=n+11) dp[i+8]=min(dp[i+8],dp[i]+m);if(i+12<=n+11) dp[i+12]=min(dp[i+12],dp[i]+l);//平行关系,不是else,因为上面执行的下面也能执行,公倍数则两个都得比较。 }//这段代码意思是不需要我们每个点都去算,而是我们只需要去算临界的节点,其它非节点都是mxfor(int i=n;i<=n+11;i++){ans=min(ans,dp[i]);//cout<<dp[i]<<' ';} cout<<ans;return 0;
}
void init(){for(int i=1;i<=n+15;i++){dp[i]=mx;}
}L
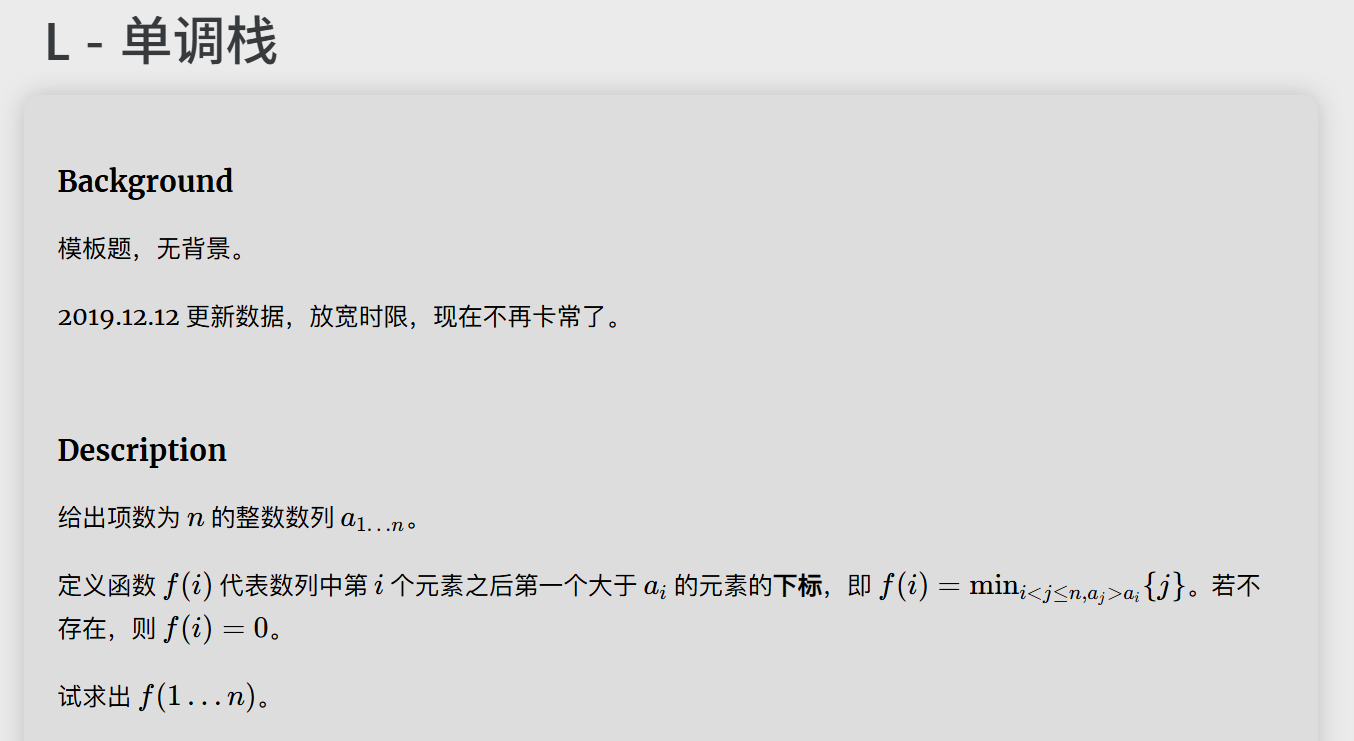
学这题最气的是,偷窥题解,结果发现没有一篇讲明白了这个题目本身和单调栈是什么关系。
好吧我资质愚钝我输了,反正这题看了好久我甚至都没看懂。
那我就来自己解释一下,以
5
1 5 2 3 4
为例子,具体讲一下这个单调栈是怎么形成的。

首先,单调栈不是存放数组本身,而是存放下标!其次,单调栈从后往前读,而不是从前往后读。
懂了这两点,就已经学会一半了。
a[5]=4,栈空,下标5入栈,此时top=1,栈含5.
a[4]=3,栈不空,但3<4(a[4]<a[stack[top]]),下标4入栈,此时top=2,栈含5 4.
a[3]=2,栈不空,但2<3(a[3]<a[stack[top]]),下标3入栈,此时top=3,栈含5 4 3.
a[2]=5,栈不空,然后我们发现a[2]>栈内任何数,所以全部出栈,然后把下标2放进来。
a[1]=1,栈不空,但1<2(a[1]<a[stack[top]]),下标1入栈,此时top=2,栈含2 1.
那么模拟了一遍,你想清楚了这和题目有什么关系吗?
单调栈是从后往前单调递减的栈,所以对于a[i],找后面更大的元素,直接看栈顶是什么就行了,因为栈顶就是比a[i]更大的元素(单调性在这里体现)所在位置的下标!!!
Code
#include<iostream>
#define i64 long long
using namespace std;
i64 n=0,a[3000010],stack[3000010],ans[3000010],top=0;
void push(i64 x);
void pop();
int main() {ios::sync_with_stdio(0);cin.tie(0);cin>>n;for(i64 i=1;i<=n;i++){cin>>a[i];}for(i64 i=n;i>=1;i--){while(top>0&&a[i]>=a[stack[top]]){pop();//弹出去,直到比栈顶更小 }//top为0表示栈空了ans[i]=stack[top];push(i);}for(i64 i=1;i<=n;i++)cout<<ans[i]<<' ';return 0;
}
void push(i64 x){stack[++top]=x;return ;
}
void pop(){stack[top]=0;--top;return ;
}M
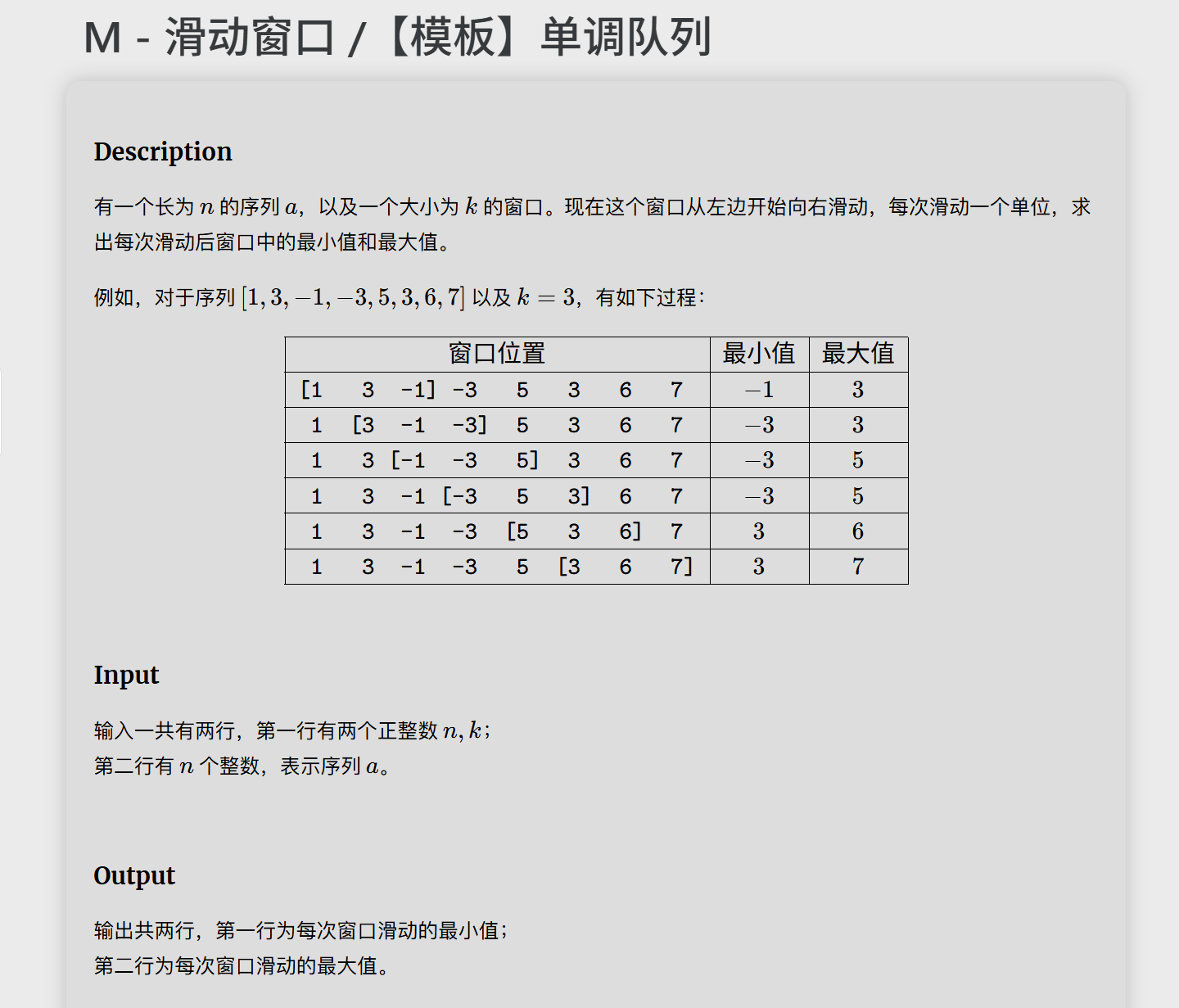
模版题,又要痛苦学习新东西。这篇题解把滑动窗口讲的非常清楚了。
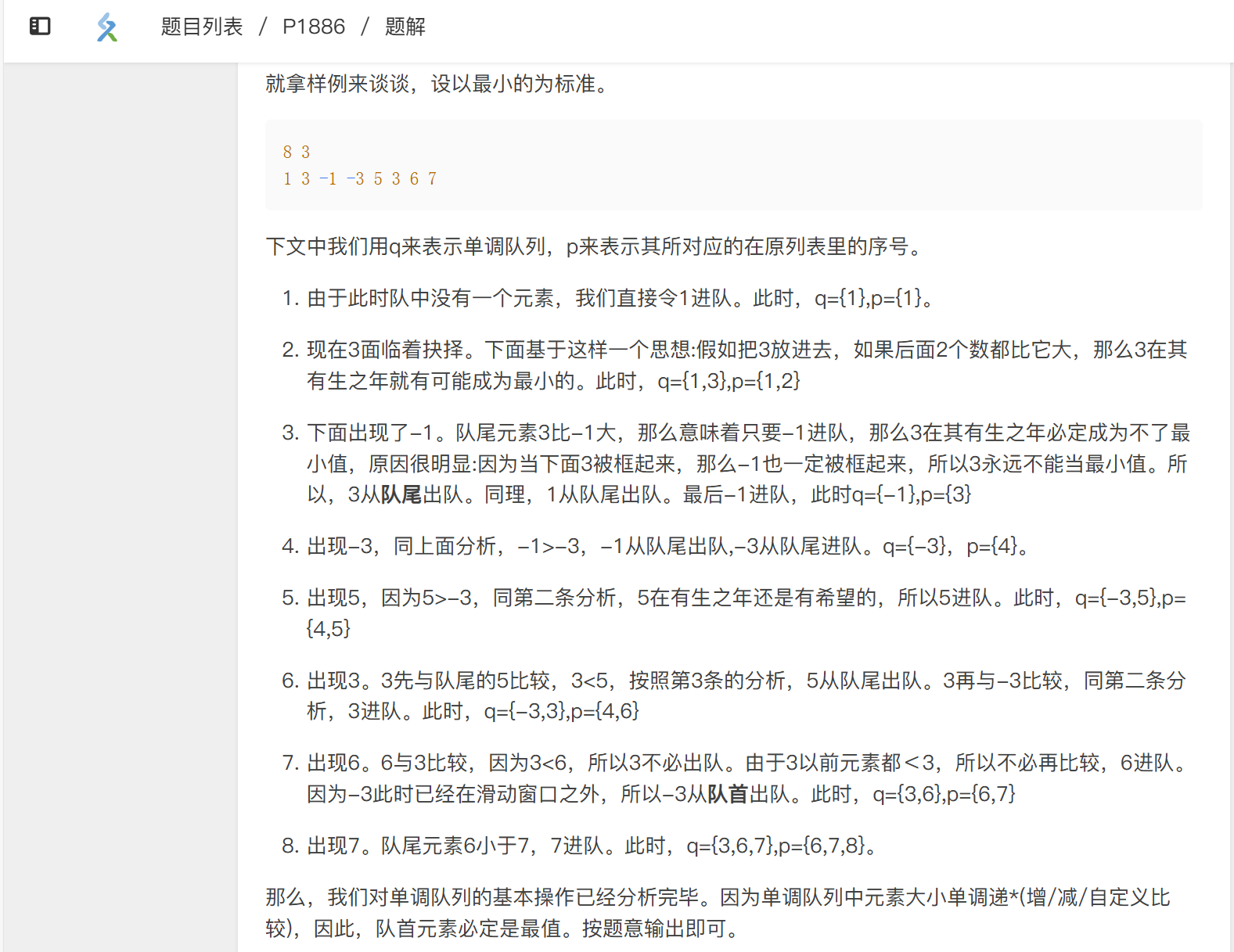
不过,实现细节其实还是非常非常复杂的,我一开始也是纯队列写,后来改成了双指针队列(省去了队首出列数组平移的操作)。再一个,head、tail的细节也非常多。
具体的细节注意我放注释里,写的很详细了,可以说一开始打模版全是坑,还需要以后的沉淀才能牢牢掌握这点。
#include<iostream>
#define i64 long long
using namespace std;
i64 n=0,k=0,a[1000010];
i64 q[1000010],head=1,tail=0,qpos[1000010];
void init();
void pop(i64 x[1000010],bool op);
void push(i64 input,i64 x[1000010]);
int main() {ios::sync_with_stdio(0);cin.tie(0);cin>>n>>k;for(i64 i=1;i<=n;i++){cin>>a[i];}//先处理最小值 for(i64 i=1;i<=n;i++){//队列q有元素,若a[i]小于等于队尾元素,就让队尾出队 while(tail>=head&&a[i]<=q[tail]){//cout<<a[i]<<' '<<tail<<' '<<q[tail]<<endl;pop(q,0);pop(qpos,0);--tail;//顺序不能错,先操作数组再把队尾--}//a[i]大于之前的元素了,那么入队 ++tail;push(a[i],q);push(i,qpos); //滑动窗口到期,队首出队 //cout<<qpos[1]<<' '<<tail<<endl;while(i-qpos[head]>=k){pop(q,1);pop(qpos,1);++head; }if(i>=k)cout<<q[head]<<' '; }cout<<endl;//再处理最大值 init();for(i64 i=1;i<=n;i++){while(tail>=head&&a[i]>=q[tail]){//只有判断条件要改 pop(q,0);pop(qpos,0);--tail;}++tail;push(a[i],q);push(i,qpos); while(i-qpos[head]>=k){ pop(q,1);pop(qpos,1);++head;}if(i>=k)cout<<q[head]<<' ';}cout<<endl;return 0;
}
void pop(i64 x[1000010],bool op){if(tail==0)return ;if(op==1){//队首出队 x[head]=0;}else if(op==0){//队尾出队 x[tail]=0;}return ;
}
void push(i64 input,i64 x[1000010]){x[tail]=input;return ;
}
void init(){head=1;tail=0;for(int i=1;i<=n;i++){q[i]=0;qpos[i]=0;}
}
P


说实话,有的题解真的治低血压。。。反正看代码之前我仍然没get到一些题解。
先来问:栈是什么栈?
这个栈是储存每个字符串操作结果的栈!!!
所以,我们应当分为一个目前的字符串s和一个字符串栈stk,这样才能保存数据。
那么和undo操作有什么关系?
出栈就代表undo操作!
这就是这题的全部逻辑,我们只需要理解到这个栈不是字符栈而是串栈就懂了。
当然还有个恶心的事情,这题卡while(cin>>n)但题目没说。。。
#include<iostream>
#include<stack>
#define i64 long long
using namespace std;
i64 n;
int main() {ios::sync_with_stdio(0);cin.tie(0);while(cin>>n){i64 op;stack<string> stk;stk.push("");for(i64 i=1;i<=n;i++){cin>>op;if(op==1){string tmp;cin>>tmp;stk.push(stk.top()+tmp);}else if(op==2){string tmp=stk.top();int k,len=tmp.length();cin>>k;tmp.erase(len-k,k);stk.push(tmp);//erase函数第一个参数是从哪个下标开始删,第二个参数表示删除几个。 }else if(op==3){int k;cin>>k;string tmp=stk.top();cout<<tmp[k-1]<<endl;}else if(op==4){stk.pop();}}}return 0;
}
Q
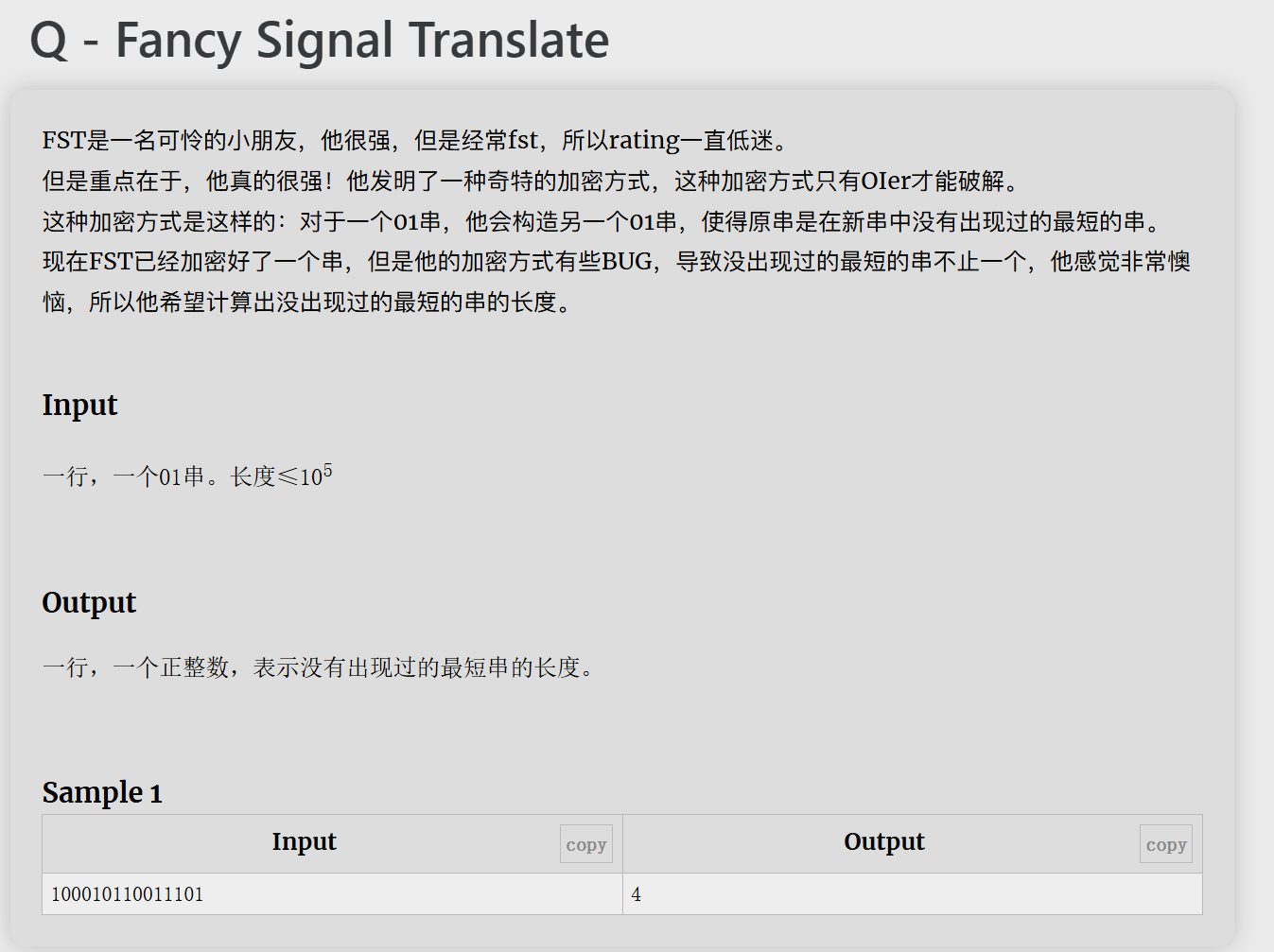
这题轮到语文发力了,不让AI做解释我是一点都看不懂题目。

而且看懂了也不会往二分答案去想。
既然都说了二分答案,那么就继续看下去吧,它是怎么实现的呢?
怎么统计出现过的字符串的呢?
它用了Map这个STL。
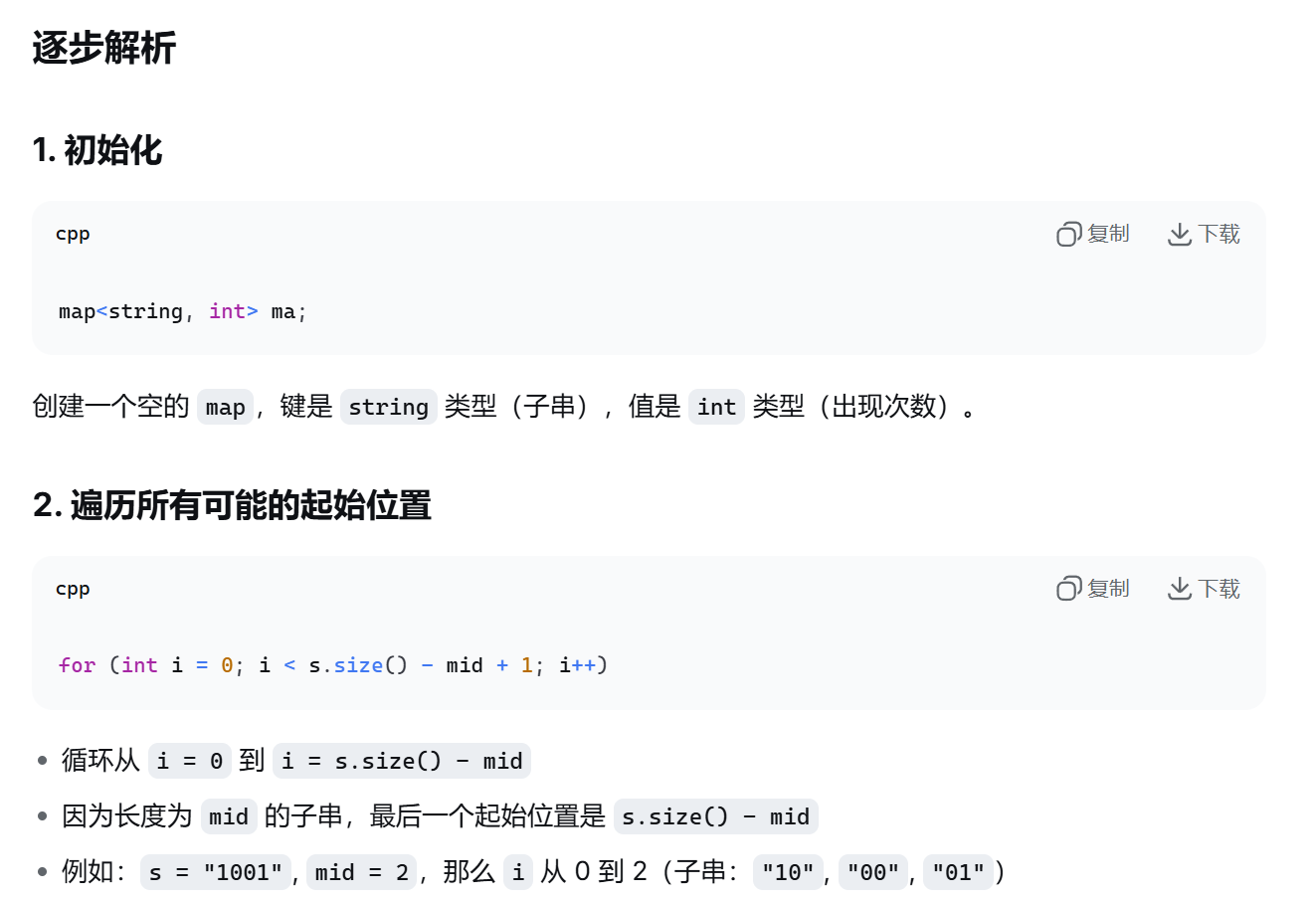
这题最大的实现细节是要返回第一个不成立的值,而不是成立的最大值。
现在学到了字符串s.substr(a,b),是从位置a开始,提取长度为b的子串。
还有练了一下左移和右移这种牛逼操作,确实简洁很多,不需要pow库了。
#include<iostream>
#include<map>
#define i64 long long
using namespace std;
i64 n,len,r=0;
string s;
void half_ans(i64 l,i64 r);
bool solve(int x);
int main() {ios::sync_with_stdio(0);cin.tie(0);cin>>s;len=s.length();while(len>=(1<<r)){r++;}half_ans(1,r);return 0;
}
void half_ans(i64 l,i64 r)
{i64 ans=0;i64 mid=(l+r)>>1;while(l<r){if(solve(mid)){//如果全部都包含,那么mid应该变大 l=mid+1;}else{r=mid;}mid=((r+l)>>1);}cout<<l<<endl;return ;
}
bool solve(int x){map<string,i64> m;for(int i=0;i<=len-x;i++){m[s.substr(i,x)]++;}if(m.size()==(1<<x)) return 1;else return 0;
}R
这题的思路我是基本上想对了,但一是我觉得不太可能搞这么复杂的东西,而是我本来也不会写树,当然G了。
所以这个树是怎么被瓜分的呢?显然应该清楚这个。这就又要到stl容器了。
我们假设有一个5的树被瓜分(超认真画图.jpg)
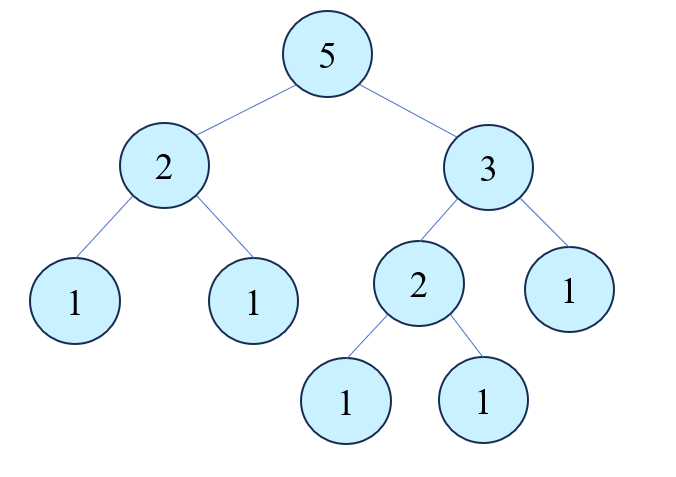
下面的树其实是不严谨的,或者说可以同级同根无序(比如3可以在2的左边也没毛病啊)
然后我们的答案可以是11111,也可以是1121甚至是113,221。也就是说不一定要到最底部可能就给分出来了。
那么怎么去对应到呢?又是map容器发力了。
我们先把所有理论的值给记录一遍,然后把树给dfs一下,看往下分分出来的值有谁不在这个map里面,那么就错了,如果全部都在map里面,大概率就是成立的。
“大概率”,因为还有一种可能,就是你的map里面多出了一些东西,比如n=5,但是要分出6个1,也就是五个玩偶分出6堆,怎么可能!所以先判定和是不是等于n。
然后操作下去,如果找到一个值,那么map[这个值]--。这个值本身能被找到,那就返回1。如果找不到,那么往下找直到分解出1,如果1也不对,那就是错了。
这题还有两个细节要注意:
我们寻找map里的数,不能直接if(map[n]),因为如果n本身不在map里,会给你创建一个键值对(n,0)出来。
如果你说创建这么个键值对,第二个数反正是0,就不影响吧?那你肯定也不知道erase函数是干啥了。
我们需要明白,分完的标志是什么?是map里面所有的值都成功归0,也就是n能被瓦解到a[i]中。
所以你的判定,不需要遍历所有的map[n]=0,而是当它为0的时候,把这个键值对从容器里删掉。
反之永远实现不了mp.size()=0。
#include<iostream>
#include<map>
#define i64 long long
using namespace std;
i64 n,m,x,sm=0;
map<i64,i64> mp;
bool dfs(i64 n);
int main(){cin>>n>>m;for(i64 i=1;i<=m;i++){cin>>x;mp[x]++;sm+=x;}if(sm!=n){cout<<"ham"<<endl;}else if(dfs(n)&&mp.size()==0){cout<<"misaka"<<endl; }else{cout<<"ham"<<endl;}return 0;
}
bool dfs(i64 n){//如果n就是要找的目标 if(mp.find(n)!=mp.end()){//不能直接写m[n],因为如果m[n]不存在会自动创建键值对(n,0) mp[n]--;if(mp[n]<=0)mp.erase(n);//如果键值对变成(n,0),那么需要删掉这个键值对本身,不然永远不会m.size()=0,只会残留一堆的键值对尾巴为0。 return 1;}//n=1而且找不到相应的匹配,那么失败 if(n<=1)return 0;if(dfs(n/2) && dfs(n-n/2))return 1;elsereturn 0;
}