当前位置：首页 > news >正文

从底层到上层的“外挂”：deque、stack、queue、priority_queue 全面拆解

news 2025/10/14 6:47:25

个人主页

🎬 个人主页：Vect个人主页

🎬 GitHub：Vect的代码仓库
🔥 个人专栏: 《数据结构与算法》《C++学习之旅》《计算机基础》

⛺️Per aspera ad astra.

在这里插入图片描述

文章目录

1. 容器适配器
- 1.1. 什么是适配器
- 1.2. 容器适配器家族
- 1.3. deque容器
- - 基本思想
  - 内存分布
  - deque的优缺点
  - 为什么选择deque作为stack和queue的底层默认容器
2. stack的模拟实现和应用
- 2.1. 模拟实现
- 2.2. 应用
3. queue的模拟实现和应用
- 3.1. 模拟实现
- 3.2. 应用
4. priority_queue
- 4.1. 功能介绍
- 4.2. 模拟实现
- - 设计模式
  - 完整实现
  - 核心：仿函数的使用
  - - 1. 纯逻辑比较/无状态仿函数
    - 2. 自定义排序逻辑：按绝对值、按长度、按字段
5. 总结
- 两种设计模式
- 容器适配器总结
- 写在最后

1. 容器适配器

1.1. 什么是适配器

生活中，适配器是两端接口不匹配的转换器

例如：旅行插头：国标->美标；Type-C转HDMI：手机/电脑->显式器；翻译：中文<->英文

都有如下共同点：不改变两端事物本身，只在中间“转一下接口/协议/形状”，让他们可以合作

回到C++设计，容器适配器的本质是一种设计模式：在已有容器之上，封装出特定用法的外壳，只暴露少量接口，不让用户随意访问修改

为什么要适配器？专注“行为”而非“存放方式”。对于一个需求的实现，我们只需要关心实现的行为“后进先出/先进先出/拿最大的先出”，而对于底层，我们无需关心

1.2. 容器适配器家族

家族成员：std::stack 、std::queue 、 std::priority_queue
默认底层结构：
1. stack<T,Container=deque<T>>
2. queue<T,Container=deque<T>>
3. priority_queue<T,Container=vector<T>,Compare=less<T>>默认是大根堆

1.3. deque容器

deque名为双端队列，是一种顺序容器

基本思想

分块存储(bloks)+指针表(map)： deque不像vector那样一整条连续的内存，而是把元素分配在若干个定长的数据块中，在用一张指针表(map)(又称中控数组)记录各个区块的地址。可以在两端扩张

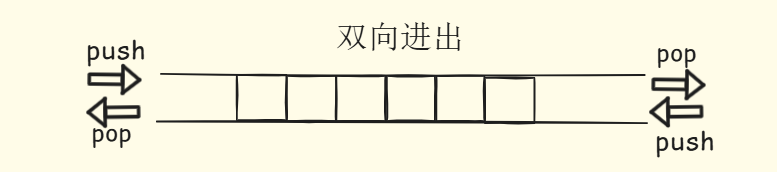
在这里插入图片描述

复杂度：
1. 随机访问operator[]: $O (1)$ ，经过指针表->块->元素的两次寻址
2. 头/尾插入删除： $O (1)$
3. 中间插入删除： $O (n)$

可以把deque想象成一条大街切割成一段段街区，手里拿着一张“街区索引表”。在两端增加删除街区很容易；若要在中间增加删除，则需要挪一串

内存分布

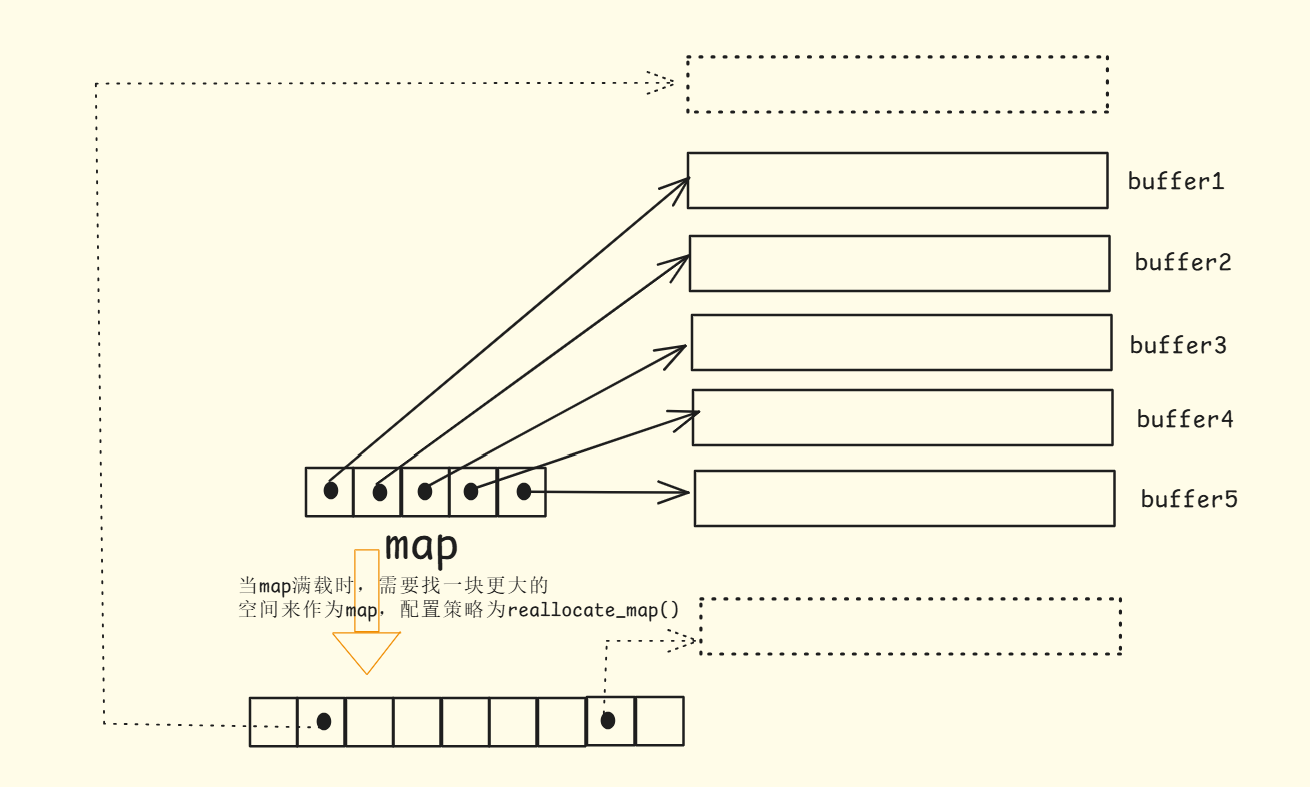
在这里插入图片描述

双端队列是一段假象的连续空间，实际上是分段连续，为了维护“整体连续”和随机访问的假象，设计了复杂的deque迭代器

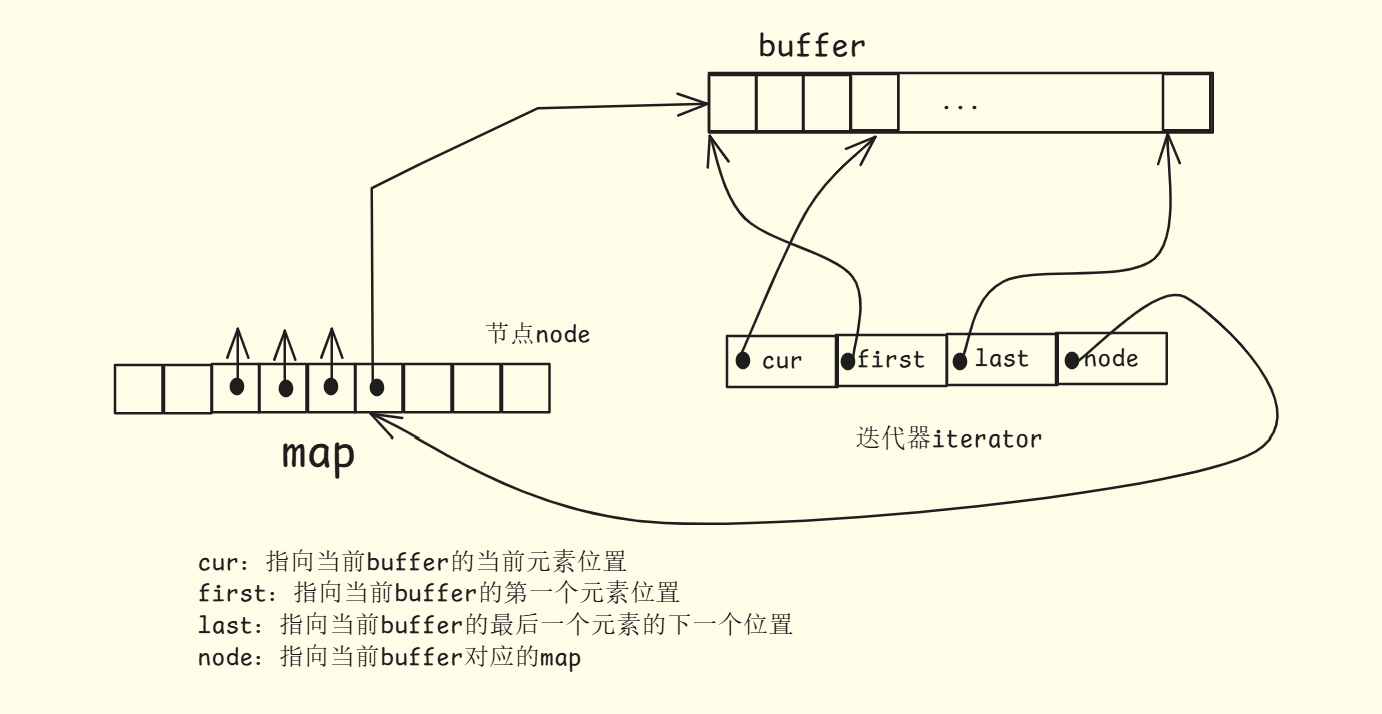
在这里插入图片描述

deque如何借助迭代器维护其假想的连续结构呢？

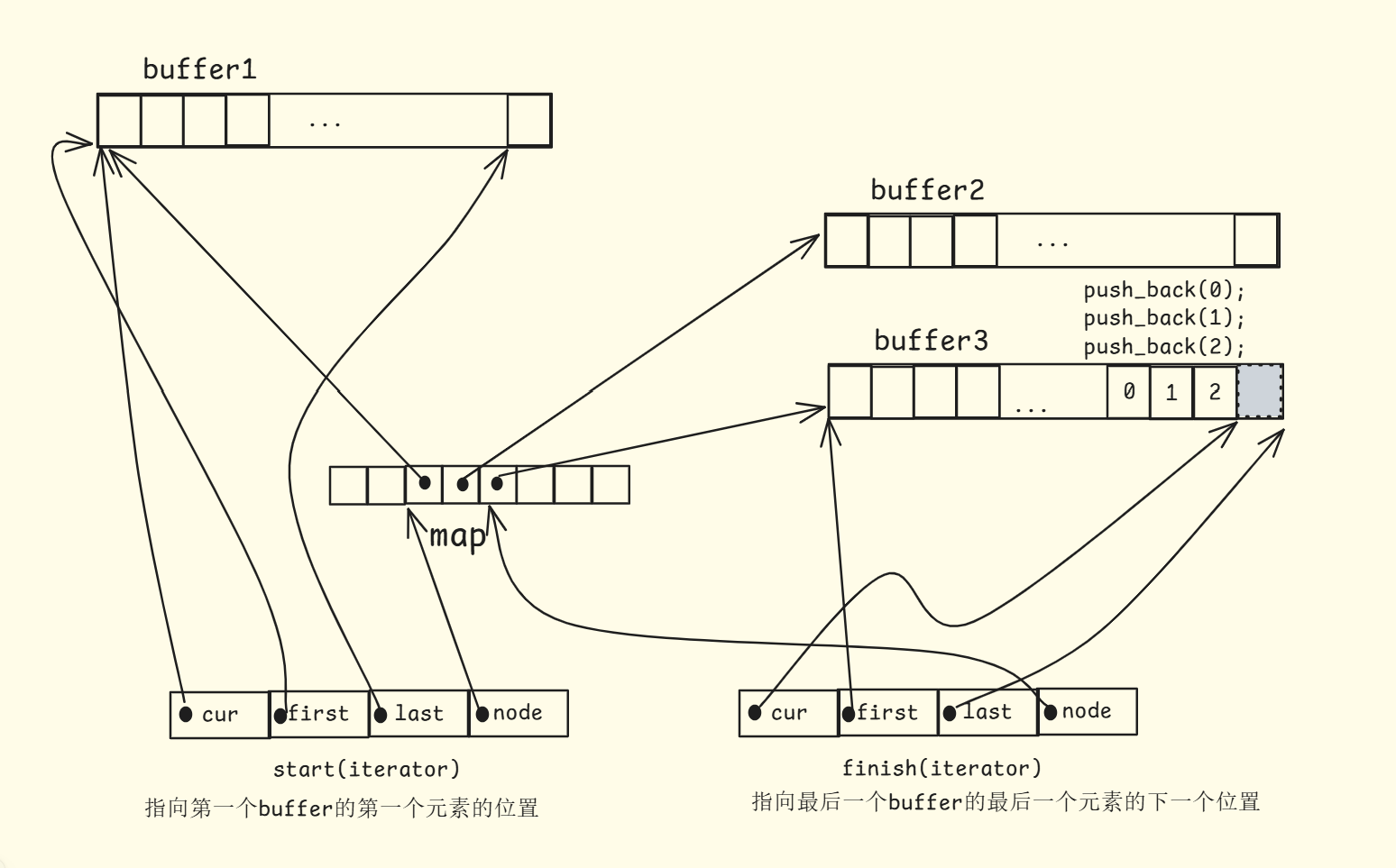
在这里插入图片描述

deque的优缺点

优势：和vector比较，头部插入删除时，不需要挪动数据，效率高，扩容时也不需要挪动大量数据，和list相比，底层是连续空间，空间利用率较高，不用存储额外字段
劣势：不适合遍历，在遍历时，deque的迭代器要频繁地检测是否移动到某段小空间的边界，导致效率低下。在序列场景下，需要经常遍历，所以选择线性结构时，优先考虑vector和list，deque主要作为satck和queue的底层结构

为什么选择deque作为stack和queue的底层默认容器

satck后进先出，因此只需要push_back()和pop_back()操作的线性结构，那么vector和list也适配，queue先进先出，因此只需要push_back()和pop_front()操作的线性结构，那么list适配。

但是STL中却采用了deque，理由如下：

satck和queue无需遍历操作（所以stack和queue没有迭代器），只需要在固定的一段或者两端操作
satck中元素增长时，deque比vector的效率高（扩容不用挪动大量数据），queue中元素增长时，deque的效率和内存使用率都很高

2. stack的模拟实现和应用

2.1. 模拟实现

对于satck更多详细介绍请看这篇文章：

从直线到环形：解锁栈、队列背后的空间与效率平衡术-CSDN博客

#pragma once
#include <iostream>
#include <deque>namespace Vect {// 第二个参数：适配器 传一个容器template <class T, class Container = std::deque<T>>class stack {public:stack(){}void push(const T& val) { _con.push_back(val); }void pop() { _con.pop_back(); }bool empty() const { return _con.empty(); }const size_t size() const { return _con.size(); }const T& top() const { return _con.back(); }T& top() { return _con.back(); }private:// 底层是容器 Container _con;};
}

2.2. 应用

155. 最小栈 - 力扣（LeetCode）

思路：用一个栈存序列所有元素，一个栈存序列的最小值

过程演示：

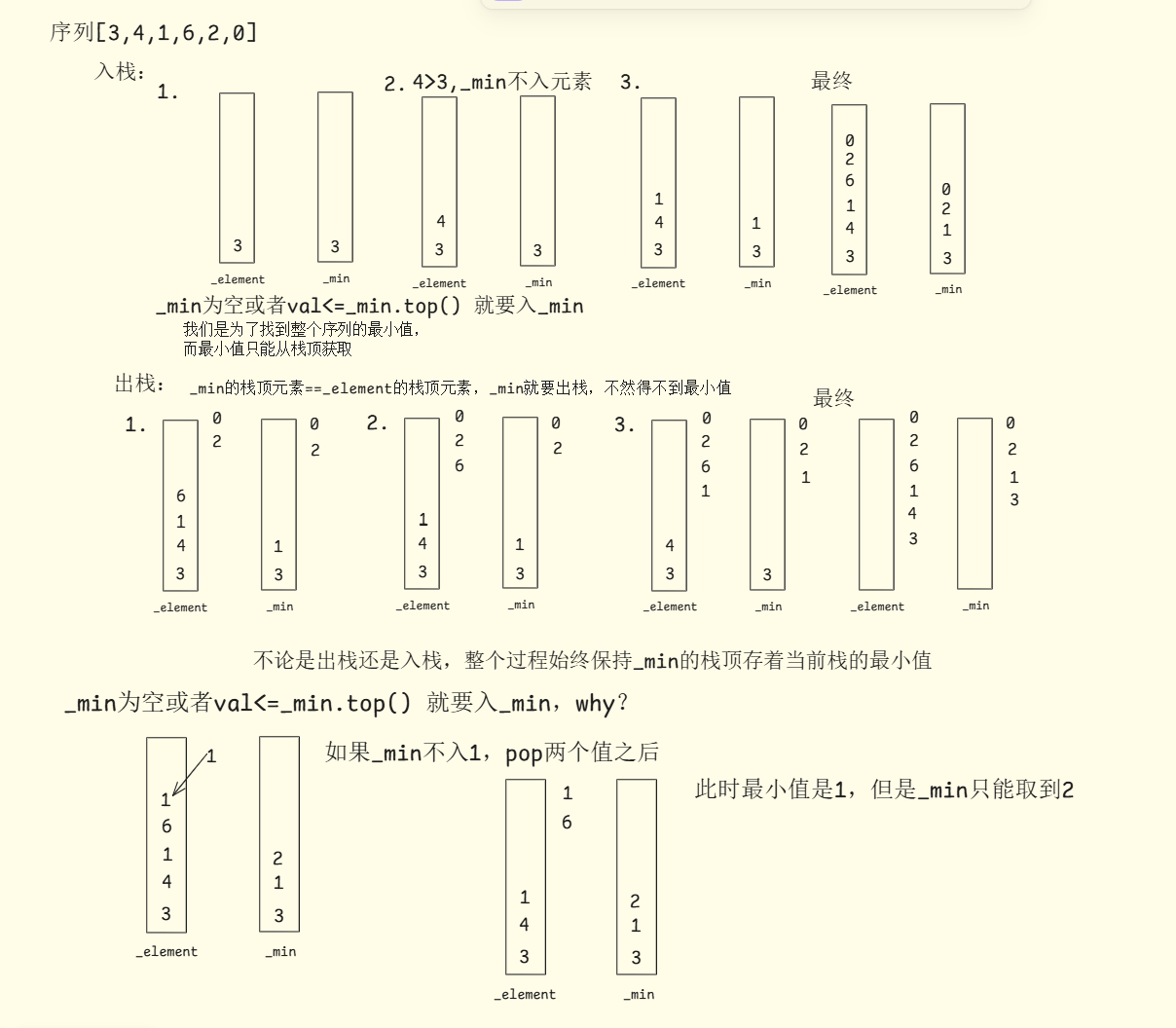
在这里插入图片描述

代码：

class MinStack {
public:MinStack() { }void push(int val) {// _min为空or_min的栈顶元素>=val 入栈if(_min.empty() || _min.top() >= val) _min.push(val);// _element正常入栈_element.push(val);}void pop() {// _min的栈顶元素==_element的栈顶元素，出栈，保证_min存的永远是当前阶段最小值if(_min.top() == _element.top()) _min.pop();_element.pop();}int top() {return _element.top();}int getMin() {return _min.top();}
private:stack<int> _element; // 存序列所有元素stack<int> _min; // 存当前序列的最小值
};

栈的压入、弹出序列_牛客题霸_牛客网

思路：

入栈序列入栈一个元素
用栈顶元素和出栈序列进行比较，会有两种情况：

栈顶元素==出栈序列当前元素，出栈序列往后遍历，弹出当前元素，回到步骤2继续
栈顶元素!=出栈序列当前元素或栈为空，回到步骤1继续

具体步骤：

在这里插入图片描述

代码：

 bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// 入栈序列和出栈序列size不同 一定不匹配if(pushV.size() != popV.size()) return false;// 定义出栈序列和入栈序列索引size_t pushIdx = 0, popIdx = 0;stack<int> st;while(popIdx < popV.size()){// 栈为空或者栈顶元素和出栈序列元素不相等 入栈while(st.empty() || st.top() != popV[popIdx]){if(pushIdx < pushV.size()) st.push(pushV[pushIdx++]);else return false;}// 栈顶元素和出栈序列元素相等 出栈st.pop();++popIdx;}return true;}
};

3. queue的模拟实现和应用

3.1. 模拟实现

对于queue更多详细介绍请看这篇文章：

从直线到环形：解锁栈、队列背后的空间与效率平衡术-CSDN博客

#pragma once
#include <iostream>
#include <deque>namespace Vect {template <class T, class Container = std::deque<int>>class queue {public:void push(const T& val) { _con.push_back(val); }void pop() { _con.pop_front(); }bool empty() const { return _con.empty(); }const T& front() cosnt { _con.front(); }T& front() { _con.front(); }const T& back() const { _con.back(); }T& back() { _con.back(); }const size_t size() const { return _con.size(); }private:Container _con;};
}

3.2. 应用

102. 二叉树的层序遍历 - 力扣（LeetCode）

思路：

利用levelSize变量获取每一层的节点数，利用队列先进先出的特性，第一层入队列，出队列前将第二层子节点带入队列，然后出队列，循环往复

代码：

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ret;if(root == nullptr) return ret;// 控制一层一层进队列size_t levelSize = 1;queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> v;// 控制一层一层出队列while(levelSize--){TreeNode* front = q.front();q.pop();v.push_back(front->val);if(front->left) q.push(front->left);if(front->right) q.push(front->right);}ret.push_back(v);// 当前层已经出完 下一层也带到了队列中levelSize = q.size();}return ret;}
};

4. priority_queue

4.1. 功能介绍

优先级队列是一种容器适配器，它的第一个元素总是所有元素中最大或最小的
本质就是堆，在堆中可以随时插入元素，并且只能检索堆顶元素（优先队列中位于顶部的元素）
底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。支持以下操作：

empty()：检测容器是否为空
size()：返回容器中有效元素个数‘
front：返回容器中第一个元素的引用
push_back()：在容器尾部插入元素
pop_back():删除容器尾部元素

4.2. 模拟实现

设计模式

底层容器： 用vector<int>存堆（连续内存+随机访问效率高）
堆的公式： 索引0是堆顶top()，对任意节点i满足：
1. 父节点：parent = (i - 1) / 2
2. 左孩子：left = 2 * i + 1
3. 右孩子：right = 2 * i + 2
Compare仿函数： 类型参数Compare(默认是less<T>)

约定：若Compare(a,b)为真，表示a的优先级低于b，于是：

默认less<T> -> 大顶堆
改成great<T> ->小顶堆

完整实现

#pragma once
#include <iostream>
#include <vector>
#include <functional>
#include <utility>namespace Vect {// 维护一个二叉堆// Compare(a,b) == true 表示a的优先级低于btemplate <class T>struct myLess {// 返回 true 表示 a 小于 b// 用途：//   1) std::sort(vec.begin(), vec.end(), myLess<int>{})  → 升序//   2) std::priority_queue<int, std::vector<int>, myLess<int>>//        使用a<b为低优先级 → 形成大顶堆bool operator()(const T& a, const T& b) const { return a < b;}};template <class T>struct myGreater {// 返回 true 表示 a 大于 b// 用途：//   1) std::sort(vec.begin(), vec.end(), myGreater<int>{}) → 降序//   2) std::priority_queue<int, std::vector<int>, myGreater<int>>//        使用a>b为低优先级 → 形成小顶堆bool operator()(const T& a, const T& b) const { return a > b;}};template <class T, class Container = std::vector<T>, class Compare = myLess<T>>class priority_queue {public:// 默认构造 priority_queue() = default;// 迭代器区间构造template <class InputIterator>priority_queue(InputIterator first, InputIterator last) {while (first != last) {_con.push_back(*first);++first;}// 建堆int n = (int)_con.size();for (int i = (n - 2) / 2; i >= 0; --i) {// 向下调整adjustDown(i);}}// 向上调整 void adjustUp(int child) {Compare comFunc;// 找父节点int parent = (child - 1) / 2;while (child > 0) {// if(_con[parent] < _con[child])if (comFunc(_con[parent], _con[child])) {std::swap(_con[parent], _con[child]);child = parent;parent = (child - 1) / 2;}else {break;}}}// 向下调整void adjustDown(int parent) {Compare comFunc;// 假设左孩子是两个孩子中更大的int child = 2 * parent + 1;while (child < (int)_con.size()) {// 假设错误//  if (child + 1 < _con.size() && _con[child] < _con[child + 1])if (child + 1 < (int)_con.size() && comFunc(_con[child], _con[child + 1])) {++child;}// 比较孩子和父亲// if (_con[parent] > _con[child])if (comFunc(_con[parent], _con[child])) {std::swap(_con[child], _con[parent]);parent = child;child = 2 * parent + 1;}else {break;}}}// 交换堆顶堆底元素 删除堆底元素 向下调整void pop() {std::swap(_con[0], _con[_con.size() - 1]);_con.pop_back();if (!_con.empty()) adjustDown(0);}// 尾插 向上调整void push(const T& val) {_con.push_back(val);adjustUp((int)_con.size() - 1);}const T& top() const { return _con[0]; }T& top() { return _con[0]; }size_t size() const { return _con.size(); }bool empty() const { return _con.empty(); }private:Container _con;};}

核心：仿函数的使用

仿函数(functor)是像函数一样可以调用的对象，本质是重载了operator()的类。好处有：

能作为模板参数的类型出现
比函数指针灵活（可以内联，实例化成对象）

1. 纯逻辑比较/无状态仿函数

// ============== priority_queue.h ============
template <class T>
struct myLess {               // a<b ⇒ a 的优先级低 ⇒ 形成【大顶堆】bool operator()(const T& a, const T& b) const { return a < b; }
};template <class T>
struct myGreater {            // a>b ⇒ a 的优先级低 ⇒ 形成【小顶堆】bool operator()(const T& a, const T& b) const { return a > b; }
};// ============== test.cpp ============
#include "queue.h"
#include "stack.h"
#include "priority_queue.h"int main() {// 大顶堆 myLess return a < bVect::priority_queue<int, std::vector<int>, Vect::myLess<int>> maxHeap;for (int arr : {5,3,1,6,20,12,60,999})maxHeap.push(arr);std::cout << "堆顶：" << maxHeap.top() << std::endl;// 小顶堆 myGreater return a > bVect::priority_queue<int, std::vector<int>, Vect::myGreater<int>> minHeap;for (int arr : {5, 3, 1, 6, 20, 12, 60, 999})minHeap.push(arr);std::cout << "堆顶：" << minHeap.top() << std::endl;return 0;
}

2. 自定义排序逻辑：按绝对值、按长度、按字段

按绝对值大的优先：

// ============== priority_queue.h ============// 按照绝对值小的排 |a| < |b|template <class T>struct absLess {bool operator()(const T& a, const T& b) const { return std::abs(a) < std::abs(b); }
};// ============== test.cpp ============
#include "queue.h"
#include "stack.h"
#include "priority_queue.h"
int main() {// -1 -10 -2 -6 -7 // 按照绝对值小的走 反而是小根堆了 如果全负数Vect::priority_queue<int, std::vector<int>, Vect::absLess<int>> absHeap;for (int arr : {-1, -10, -2, -6, -7})absHeap.push(arr);std::cout << "堆顶：" << absHeap.top() << std::endl;for (size_t i = 0; i < absHeap.size(); i++){std::cout << absHeap[i] << " ";}return 0;
}

按字符串长度大的优先：

// ============== priority_queue.h ============// 按字符串长度大的优先 a.size() < b.size()struct strLess {bool operator()(const std::string& a, const std::string& b) {return a.size() < b.size();}};// ============== test.cpp ============
#include "queue.h"
#include "stack.h"
#include "priority_queue.h"
int main() {// 按字符串长度大的优先 a.size() < b.size()Vect::priority_queue<std::string, std::vector<std::string>, Vect::strLess> strHeap;for (std::string strArr : {"nihao", "hhh", "1234", "1433223"})strHeap.push(strArr);std::cout << "堆顶：" << strHeap.top() << std::endl;return 0;
}

按照结构体规则排序：

// ============== priority_queue.h ============// 按照结构体比较 分数高的优先 分数相同的按照名字字典序优先struct StudentInfo {int score;std::string name;};struct structLess {// 返回 true 表示 左操作数 优先级 低 于 右操作数bool operator()(const StudentInfo& stuA, const StudentInfo& stuB) const {if (stuA.score != stuB.score) return stuA.score < stuB.score; // 分数高的优先return stuA.name > stuB.name; // 分数相同，name 小的优先（ASCII 小在前）}};
// ============== test.cpp ============
#include "queue.h"
#include "stack.h"
#include "priority_queue.h"
int main() {// 按照结构体比较 分数高的优先 分数相同的按照名字字典序优先Vect::priority_queue<Vect::StudentInfo,std::vector<Vect::StudentInfo>, Vect::structLess> structHeap;for (const Vect::StudentInfo& stu :std::initializer_list<Vect::StudentInfo>{{91,  "coke"},{50,  "hhh"},{100, "1234"},{100, "22"}}) {structHeap.push(stu);}std::cout << "堆顶：" << structHeap.top().score<< " " << structHeap.top().name << std::endl;return 0;
}

5. 总结

两种设计模式

截至目前，我们已经掌握了两种设计模式： 迭代器和适配器

迭代器：
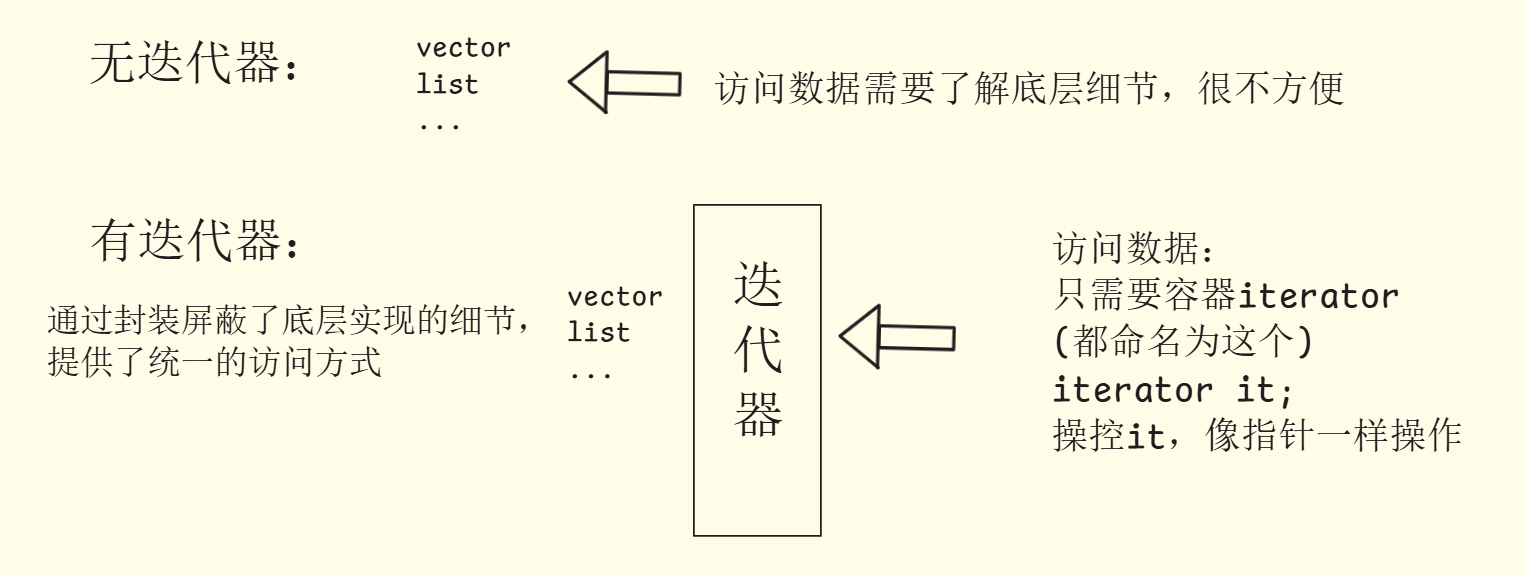
**容器适配器：**核心作用是转换，将一个类的接口转换成用户所期望的另一个接口，而不修改底层细节，也无需关心底层细节，这也是封装的思想

容器适配器总结

适配器	底层默认容器	数据结构	功能
`stack`	`deque`	栈（先进后出）	只允许在一端（栈顶）插入(`push`) 删除(`pop`) 访问(`top`)数据
`queue`	`deque`	队列（先进先出）	允许在两端，队头删除(`pop`）、队尾插入(`push`)数据，两端都可访问数据(`front和back`)
`priority_queue`	`vector`	堆（优先级队列）	元素出队顺序按照优先级（默认大根堆），从堆顶出数据）