机器学习：支持向量机

支持向量机的介绍

来源：图片来源:BiliBili-数之道

概念

支持向量机(Support Vector Machine,SVM)是常用的分类算法之一。其目标是找到一个最优的决策边界，这个边界能够最大程度的将不同类别的样本分离开。 关键是找到最大决策边界，即不仅要完成分类正确，还要让样本距离这个决策边界尽可能的远。

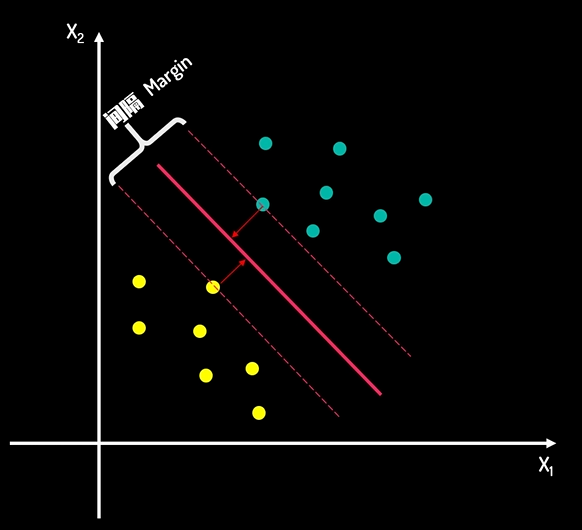
根据图片，就把一个分类问题转换为一个“求最大间隔”问题。间隔的正中间就是“决策边界”，当有新数据需要判断时，即可看对应的数据处于决策边界的哪一侧。而两侧的距离决策边界最近的点构成的平行线称为“支持向量”。

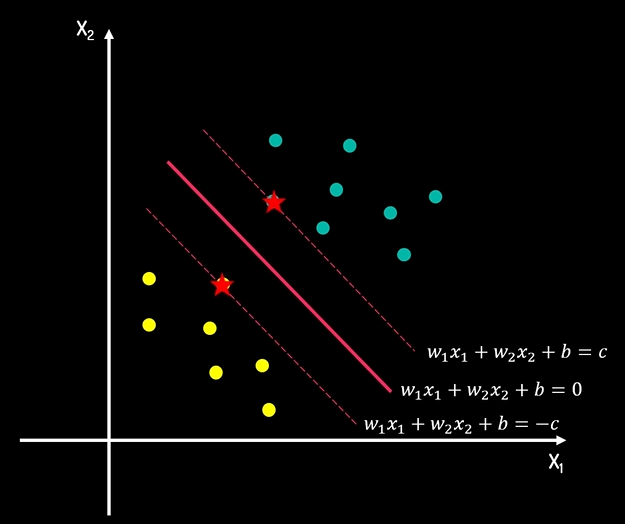
软间隔和硬间隔

在进行分类任务的时候，大多数情况下很难找到上图类似的理想线性可分的样本点。

1.硬间隔：理想化的完美世界

假设：数据是完美线性可分的
目标：找到一条超平面，能够100%正确分类所有样本
要求：所有样本都必须正确分类，且距离决策边界至少有一定距离

2.软间隔：面对现实的妥协

承认：现实数据可能存在噪声、异常值、重叠
目标：在尽可能正确分类和保持较大间隔之间取得平衡
允许：少数样本可以出现在“错误的一侧”或者距离决策边界很近

3.惩罚因子

上述描述在软间隔内，允许部分点出现错误，那么怎么进行衡量呢？主要使用到惩罚因子C；
(1)当$C\to \infty$时，软间隔接近硬间隔，不允许出现任何错误，容易出现过拟合；
(2)当$C\to 0$时，间隔可以无限放款，几乎不关心分类的正确性，可能出现欠拟合。
所以在训练SVM模型时，需要选取适中的C，在间隔宽度和分类错误之间取得平衡。

核函数

当在处理分类问题时，如果低维平面无法确定一个核函数，可以利用核函数对问题进行升维处理。核函数允许SVM在高维特征空间中学习线性决策边界，而无需显式计算高维映射，从而避免“维度灾难”。

1.线性核linear

特点：
(1)最简单、计算效率最高
(2)可解释性强
(3)只有一个超参数(惩罚因子C)
适用场景
(1)特征维度很高(如文本分类)
(2)数据近似线性可分
(3)需要快速训练和预测
(4)作为基线模型

2.多项式核poly

超参数说明：
(1)degree:多项式次数，控制复杂度
(2)gamma:缩放因子，默认scale
(3)coef0:常数项，控制偏置
特点：
(1)可以学习多项式决策边界
(2)多项式次数越大，模型越复杂，容易过拟合
(3)需要仔细调参(3个参数)
适用场景:
(1)数据存在明显的多项式关系
(2)需要中等复杂的非线性边界
(3)有先验知识表明数据适合多项式拟合

3.径向基核RBF- 最常用

特点：
(1)最常用、最强大的非线性核
(2)将数据映射到无限维特征空间
(3)具有局部性：仅附近样本点影响决策
(4)需要特征标准化（对尺度敏感）
适用场景：
(1)大多数非线性问题的首选
(2)没有先验知识关于数据分布时
(3)图像识别、复杂模式识别

网格搜索

网格搜索是一种通过穷举搜索预先定义的参数组合，来寻找最佳超参数的方法。它就像在一个"网格"上逐个尝试所有可能的参数组合。
核心思想：
(1)为每个超参数定义一组候选值
(2)尝试所有可能的组合
(3)使用交叉验证评估每种组合的性能
(4)选择性能最好的参数组合

SVM实现

实现分类

import matplotlib.pyplot as plt
# sklearn实现svm
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,classification_report
# 1.生成数据
data = {'学习时长': [5, 3, 5, 6, 3, 4, 5, 4, 6, 3, 5, 4, 6, 3, 5, 4, 6, 5, 3, 4],'做题数量': [20, 10, 15, 25, 5, 18, 22, 8, 20, 12, 9, 15, 28, 7, 17, 11, 6, 19, 13, 14],'是否通过': [1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
}
# 转换为pandas
data = pd.DataFrame(data)
X = data[['学习时长','做题数量']].values
y = data['是否通过'].values
# 2.数据集切分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42,shuffle=True)
# 3.定义网格搜索
param_grid = {'kernel':['rbf','linear','poly'],'C':[0.5,1.0,1.1,1.2,2.0,1.5]
}
base_model = SVC()
model = GridSearchCV(estimator=base_model,param_grid=param_grid,cv=5,scoring='accuracy',verbose=1)
# 4.模型训练
model.fit(X_train,y_train)
# 5.查看分类效果
pred_data = model.predict(X_test)
print(f'准确率为:{accuracy_score(y_test,pred_data):.3f}')
print(f'召回率为:{recall_score(y_test,pred_data):.3f}')
print(f'精确率为:{precision_score(y_test,pred_data):.3f}')
print(f'混淆矩阵:\n{confusion_matrix(y_test,pred_data)}')
print(f'分类报告:\n{classification_report(y_test,pred_data)}')
print(f'最佳预估器分类参数:{model.best_params_}')
# 画图显示
passes_data = data[data['是否通过']==1][['学习时长', '做题数量']]
deny_data = data[data['是否通过']==0][['学习时长', '做题数量']]
plt.figure(figsize=(12,5))
plt.scatter(passes_data['学习时长'],passes_data['做题数量'],label='pass',color='red')
plt.scatter(deny_data['学习时长'],deny_data['做题数量'],label='deny',color='black')
plt.xlabel('Learning_Time')
plt.ylabel('Number_Question')
plt.legend()
plt.show()

输出如下：

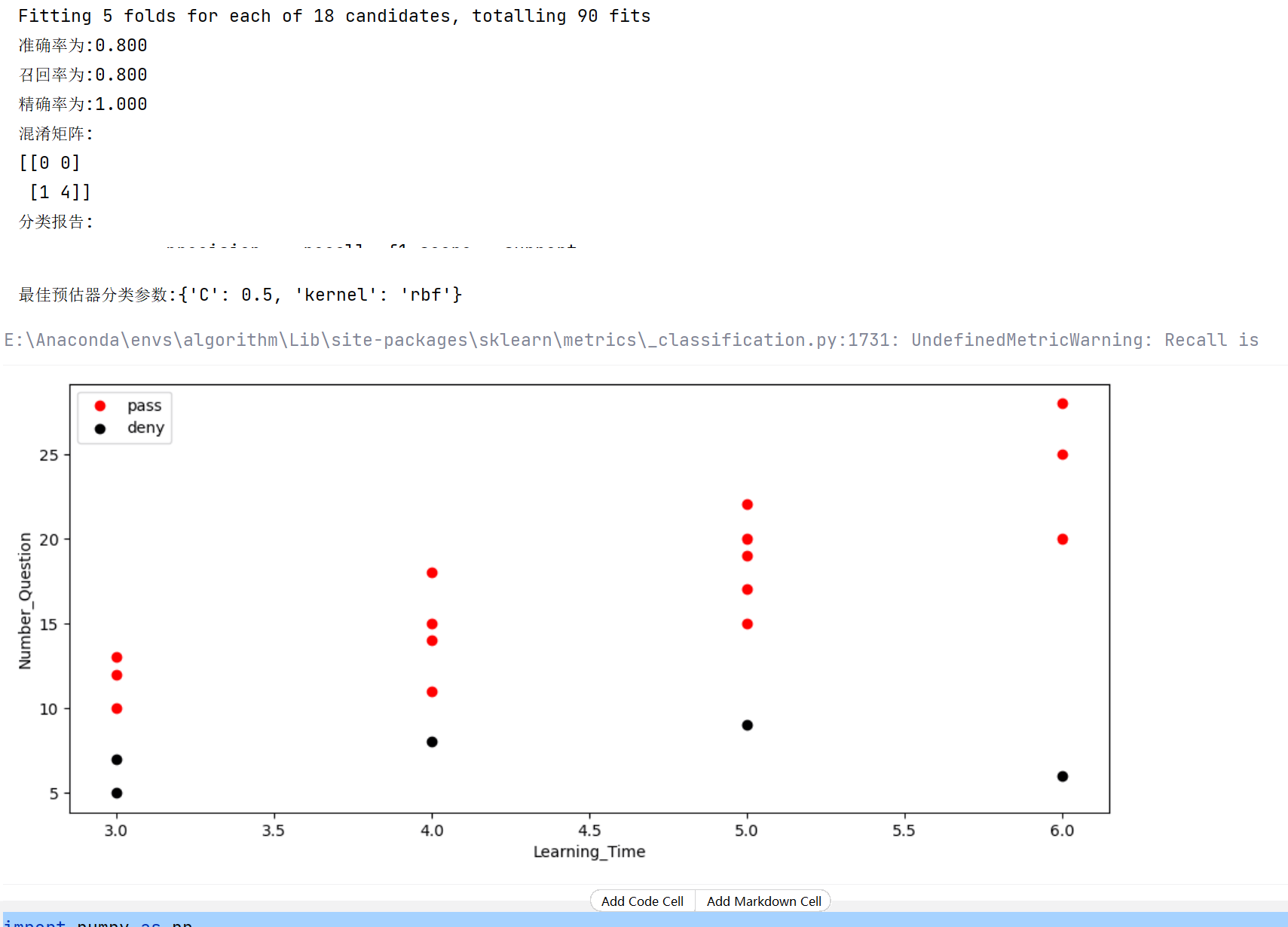
实现回归

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler# 1. 生成模拟数据
np.random.seed(42)
study_hours = np.random.uniform(1, 10, 100)  # 学习时长 (1-10小时)
# 模拟考试成绩 = 10*学习时长 + 随机噪声
exam_score = 10 * study_hours + np.random.normal(0, 5, 100)# 2. 数据整理
data = pd.DataFrame({'学习时长': study_hours,'考试成绩': exam_score
})# 3. 数据标准化（只对特征进行标准化）
scaler = StandardScaler()
X = scaler.fit_transform(data[['学习时长']])  # 只使用学习时长作为特征
y = data['考试成绩']# 4. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 5. 训练 SVR 模型
svr = SVR(kernel='linear', C=1.0, epsilon=0.1)  # 使用RBF核
svr.fit(X_train, y_train)# 6. 预测
y_pred = svr.predict(X_test)# 7. 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
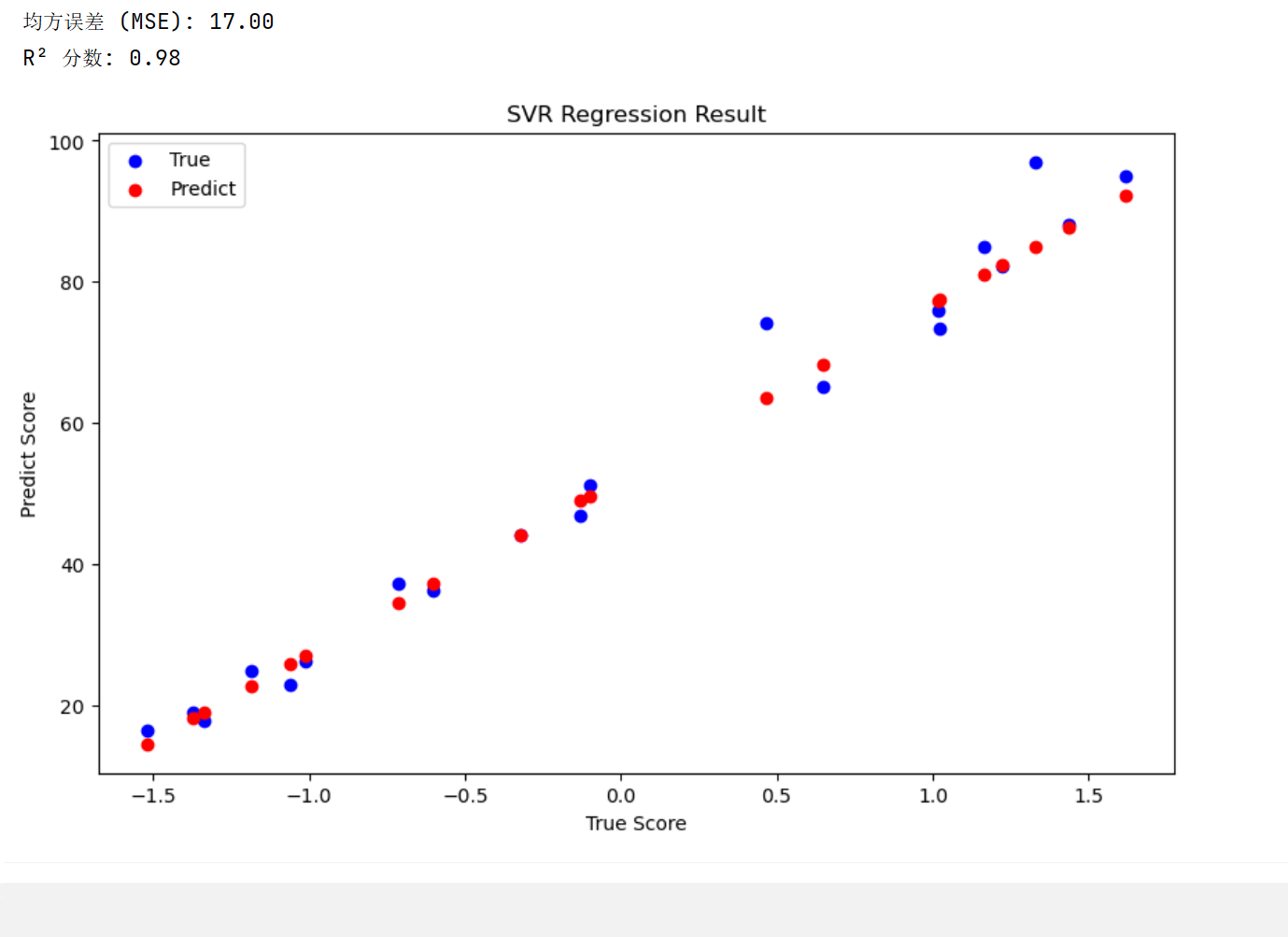
print(f"均方误差 (MSE): {mse:.2f}")
print(f"R² 分数: {r2:.2f}")# 8. 可视化预测结果plt.figure(figsize=(10, 6))
plt.scatter(X_test, y_test, color='blue', label='True')
plt.scatter(X_test, y_pred, color='red', label='Predict')
plt.xlabel("Stander Time")
plt.ylabel("Score")
plt.title("The Relation of Study Time & Score")
plt.legend()plt.xlabel("True Score")
plt.ylabel("Predict Score")
plt.title("SVR Regression Result")
plt.legend()
plt.show()

输出如下：