GESP C++等级认证三级14-原码反码补码2-1

计算机中的数据都是以二进制方式存在的。对于程序中的整数，计算机可以通过原码、反码和补码等方式进行存储。

1 原码

1.1 表示方式

用原码表示整数的方法为，最高位表示该整数的符号，0表示正数，1表示负数，其余位表示该整数的数值（二进制形式）。以8位二进制数为例，5和-5的原码分别如图1所示。

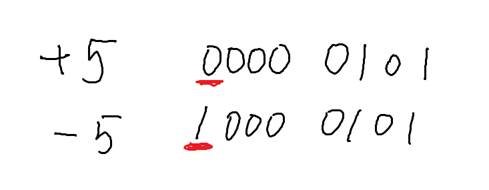
图1 +5和-5的原码表示方式

1.2 加法计算

如果计算机使用原码的方式保存整数，在进行整数的加法计算时，两个整数相加或者两个负数相加是没有问题的，如图2所示。

图2 使用原码进行正整数和负整数相加

从图2中可以看出，使用原码计算5+5或者-5+（-5）是没有问题的。但是当计算一个正整数与一个负整数相加时，就会出现问题，如图3所示。

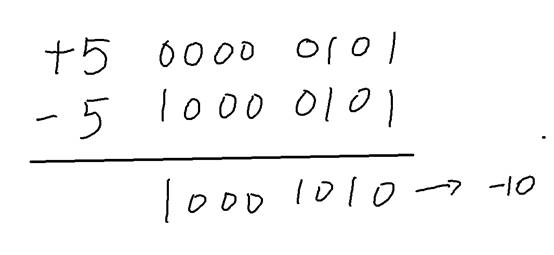
图3 使用原码进行正整数与负整数的相加

从图3可以看出，使用原码计算5+（-5）时，得到的答案是-10，很明显结果是错误的。

1.3 取值范围

当使用一个8位二进制原码时，其表示的最小整数是“11111111”，即-127，最大整数是“0111 1111”，即127。所以8位二进制原码的取值范围是-127~127，这个范围内有255个整数。但是8位二进制原码可以有256种取值，主要原因是，在表示0时，存在+0和-0两种情况，即“0000 0000”和“1000 0000”。

2 反码

2.1 表示方式

使用反码能够解决正整数与负整数相加的问题。正整数的反码与其原码相同，负整数的反码是在其原码的基础上，符号位不变，数值位按位取反，如图4所示。

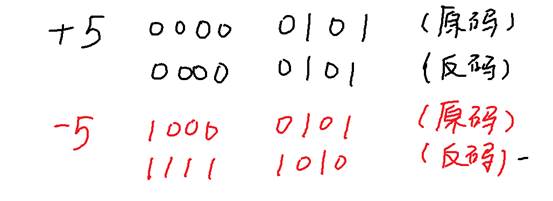
图4 正整数与负整数的反码

相关链接1 负数反码的另外一种求法，先获取该负数的绝对值，之后将绝对值按位取反，就可以得到该负数的反码。

2.2 加法计算

使用反码计算正整数与负整数相加问题，如图5所示。

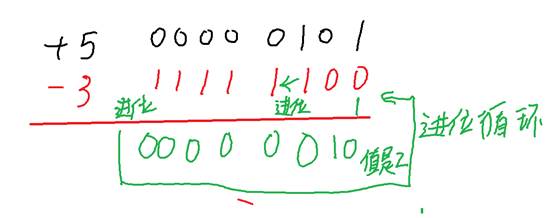
图5 使用反码进行正整数和负整数相加

其中，反码相加使用了“进位循环”的方式，即最高的进位循环到最低位使用。5+（-3）的结果是2，结果正确。但是由于反码的这种“进位循环”，导致计算效率不高。

2.3 取值范围

使用8位二进制反码表示整数时，也存在+0和-0问题。+0的反码是“0000 0000”，而-0的反码是“1111 1111”，所以8位二进制反码的取值范围是-127~127。