LDPC 码基本概念

        低密度奇偶校验(LDPC) 码是一类线性分组码，名字中低密度来源于其校验矩阵的稀疏性，即校验矩阵中只有数量极少的非零元素。

        众所周知，所有线形分组码都可用其校验矩阵或者Tanner 图表示。其中N为码长，K为信息位长度，M为校验位长度。

        Tanner 图由两类节点组成：变量节点(Variable node) 和校验节点(Check node)，分别对应于校验矩阵中的M行和N列。

        其中，同一类节点之间没有连线，不同类两点之间才可能有连线，该连线意味着该变量比特参加了此校验方程，也对应着校验矩阵某一行中‘1’ 的位置。

        假设一个(8,4) 线性分组码的校验矩阵如下式所示

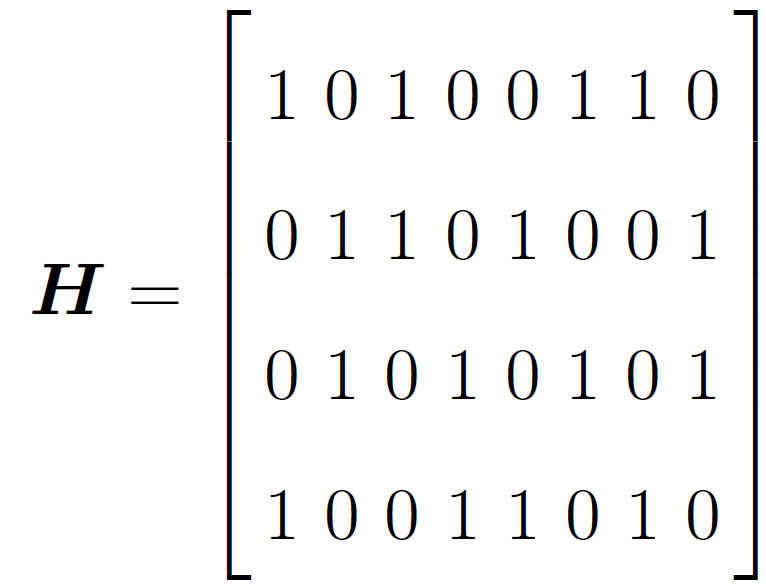
        对应的Tanner 图如下所示

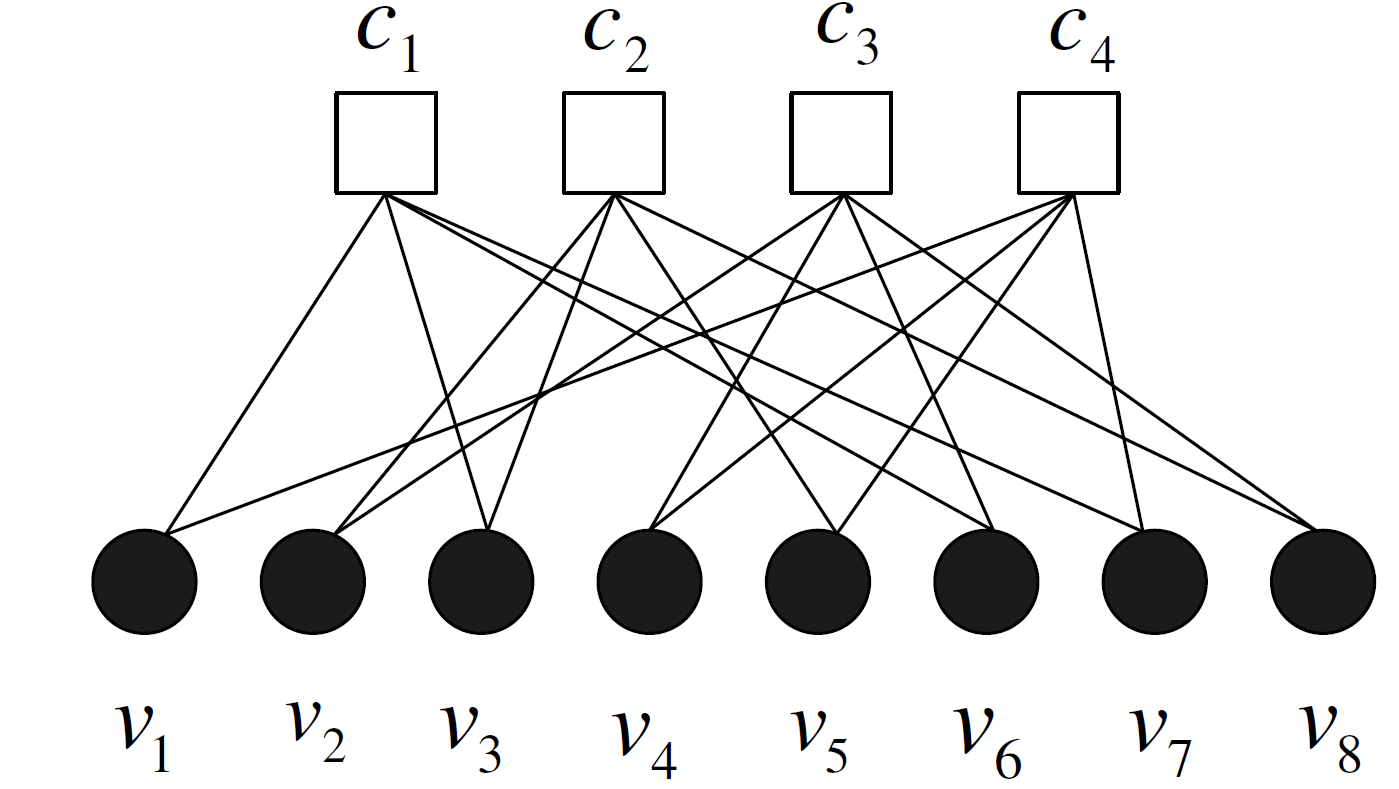
        另外Forney 于2001 年提出的Forney 型因子图如下所示。

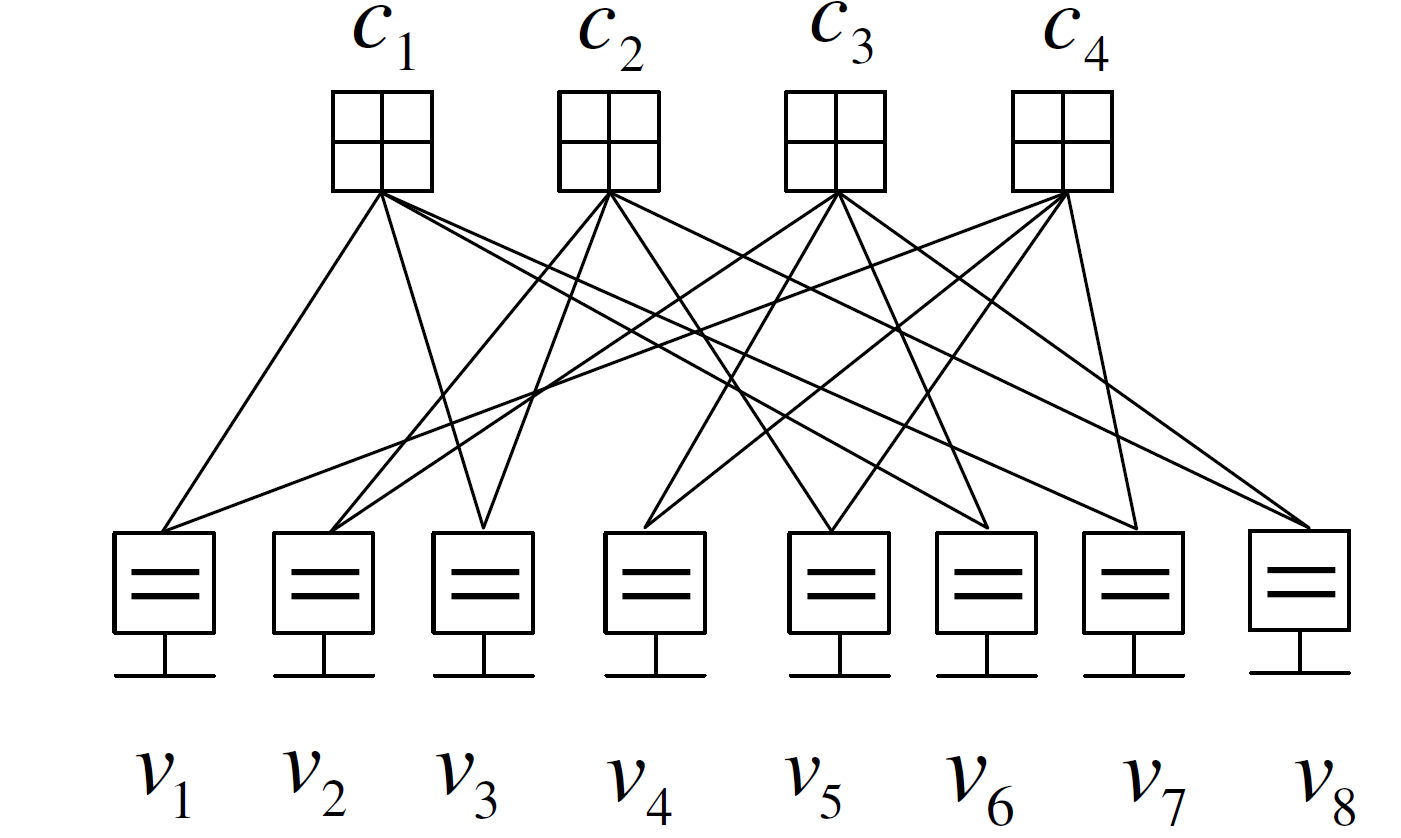
对于定义在有限域GF(q) 上的q元LDPC 码，其校验矩阵仍然满足前述稀疏性，区别在于校验矩阵中的非零元由‘1’ 替换为限域GF(q) 上的非零元。

        仍然对应(8,4) 线性分组码的例子，其Tanner 图结构不变，只不过每条连线还要加一个数值，用来代表多元码的对应非零元素取值。

        多元LDPC 码的Forney 型因子图变化较大，每一个多元符号相对于引入了一个等价的符号交织器，其结构如图所示。

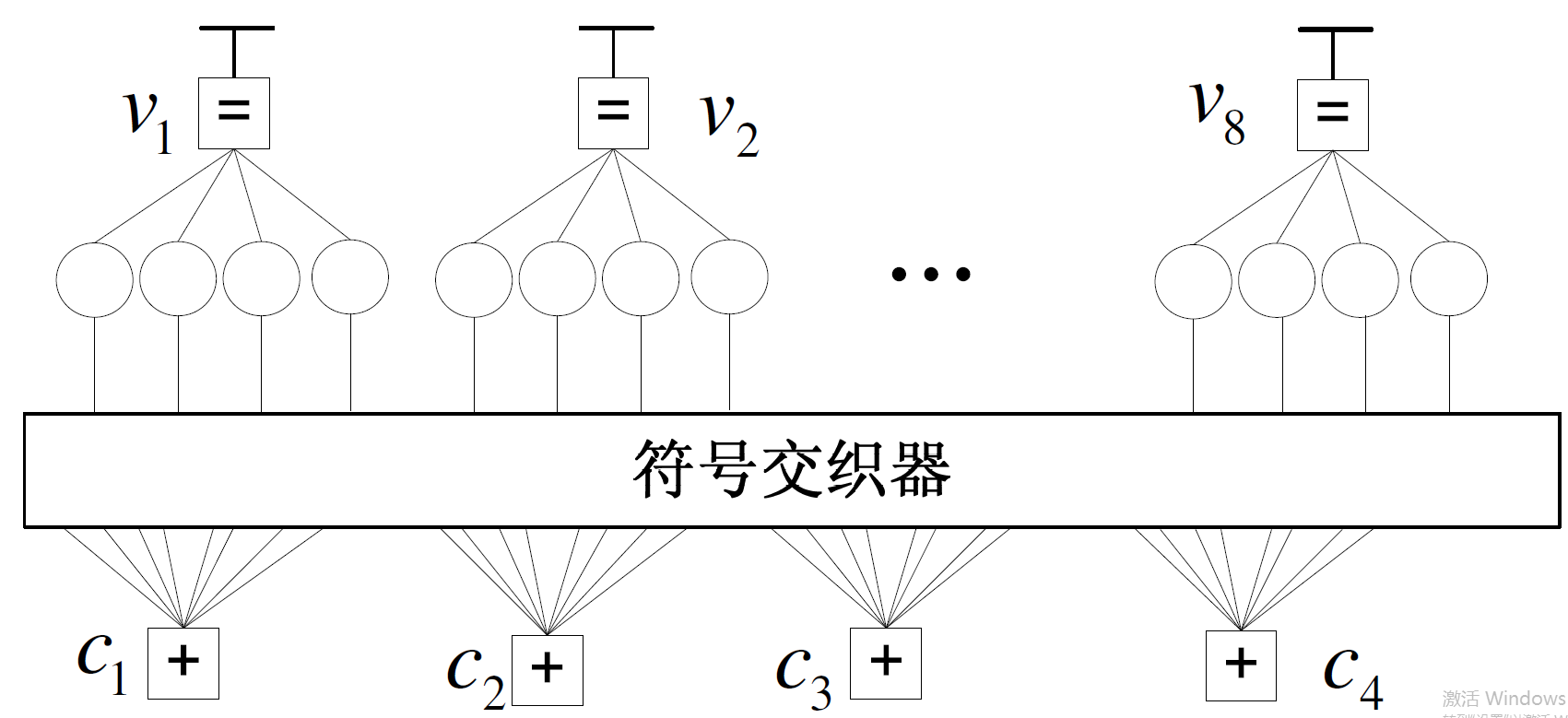
从上面的例子可以看出，该码的行重和列重都相等。对于这样的LDPC 码，很容易用其行重列重来标记，称为规则LDPC 码，例如(4,8) 码。对于行重和列重不等的码，称为非规则LDPC 码，需要用度分布多项式λ(x) 和ρ(x) 来表示。

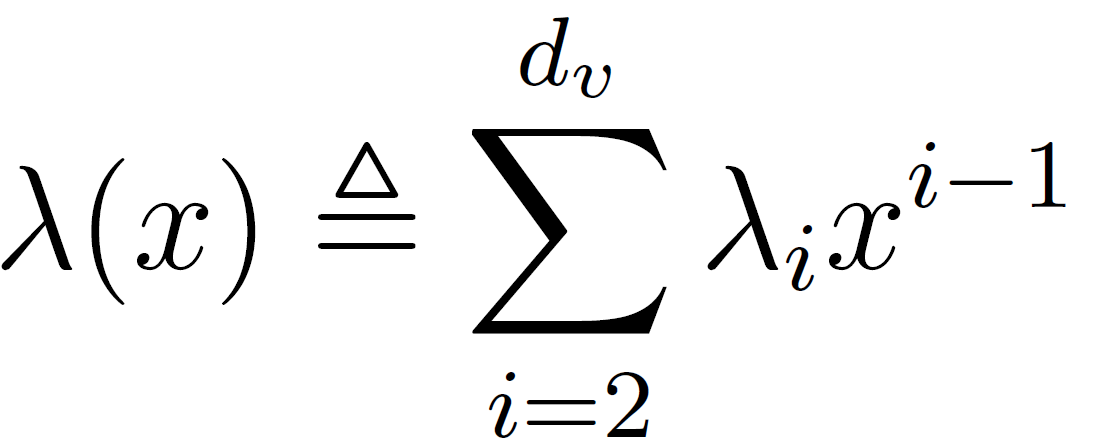
        其中，表示所有与度为i 的变量节点相连的边数占图中总边数的比例，为最大的变量节点度。类似地，在多项式中，表示所有与度为i 的校验节点相连的边数占图中总边数的比例，为最大的变量节点度。例如，(4, 8) 规则LDPC 码具有度分布。

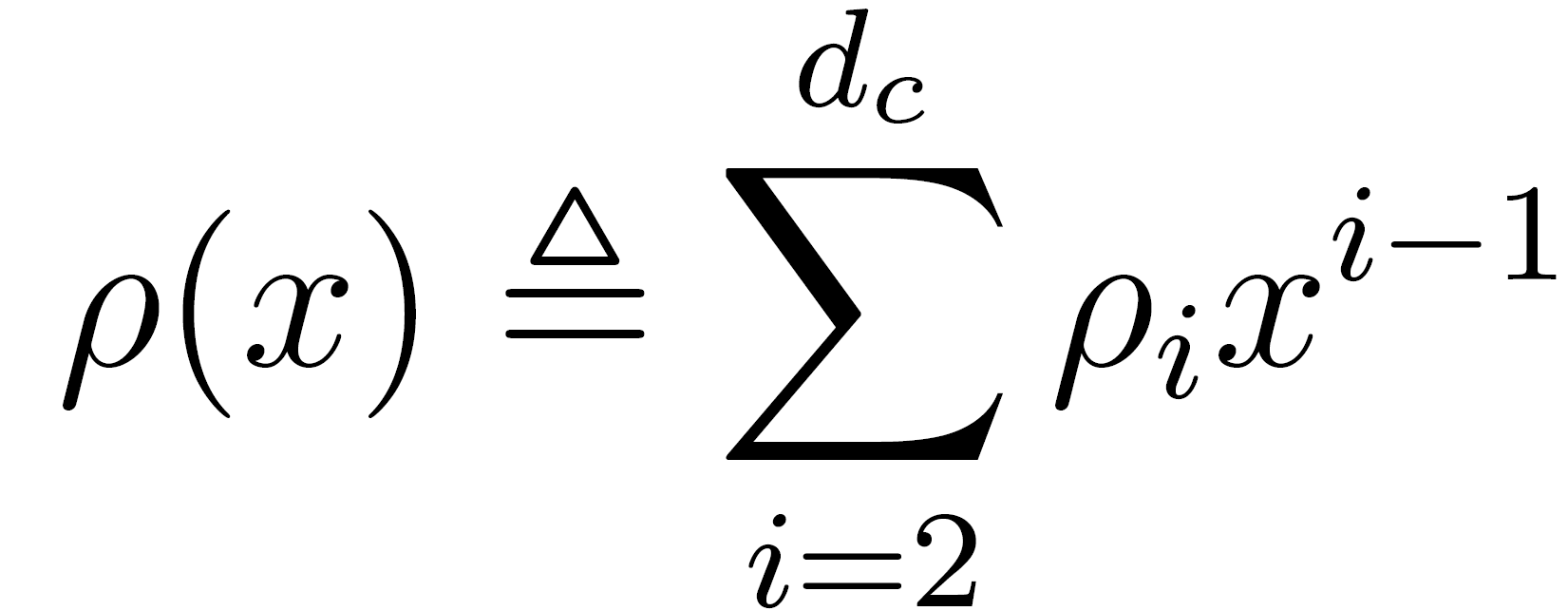
        LDPC 码还有另外一个重要的概念，称为环长或者围长(girth)。环是指LDPC 码Tanner 图中，任选其中一个节点作为起始节点单向遍历此路径，最后必返回所选的节点，整个路径就是一个环。

        而环长指的是环上的节点数或边数，它是影响LDPC 码性能的一个重要因素。

        现有研究结论表明：无环图可以确保LDPC 码的最常用译码算法—和积算法的最优性，但无环图并不支持好码的存在。

        从理论上讲，二者显然是一对矛盾，那么应该怎么对待LDPC 码中的环呢？

        在实践中，人们发现：设计好码的一个关键之处就在于使码的环长尽量大，从而使迭代译码在有限次迭代中不受环的影响，从而和积算法也近似地工作在一个局部无环图上，进而实现近似的最优译码。