当前位置：首页 > news >正文

密码学系列 - 零知识证明(ZKP) - MSM运算

news 2025/10/13 7:04:46

零知识证明(MSM与模乘) - FPGA vs. GPU

多标量乘法（MSM）包括大量的椭圆曲线标量乘法运算, 但不包括多项式乘法

MSM主要用于高效计算多个标量和椭圆曲线点的乘积和，形式为 $_{i=1}^{n} a_i P_i$ ，其中 $a_i$ 是标量， $P i$ 是椭圆曲线上的点。这个运算在 zkSNARK 等零知识证明系统中广泛应用，用于验证电路和多项式评估的结果。

下文会用Aleo中的一些算法举例

Aleo的ZKP使用Marlin协议和KZG多项式承诺
Aleo的ZKP用Marlin取代Groth16, 一次可信设置, 能应用于任一公式
Marlin 的算术语言允许 R1CS(加法和乘法电路), 涉及三个矩阵
参考链接

1. MSM在挖矿中的作用

在 Aleo 的挖矿过程中，矿工通过执行智能合约电路并生成 zkSNARK 证明来完成挖矿任务。生成 zkSNARK 证明的过程涉及以下步骤：

电路执行：矿工运行智能合约对应的电路，获取电路中的中间变量和输出结果。
MSM 运算：使用 MSM 来处理电路中所有的标量乘法和椭圆曲线点乘累加运算。电路执行过程中产生的标量会与预定义的椭圆曲线基点进行乘法运算，MSM 将所有这些标量乘法运算累加，生成证明所需的加密承诺。
生成 zkSNARK 证明：通过 MSM 生成的加密承诺将被用于最终的 zkSNARK 证明生成器，矿工使用这些证明来证明区块的有效性，并提交到网络进行验证。
提交和验证：矿工将生成的 zkSNARK 证明与工作量证明一并提交到网络。其他节点将使用验证算法来快速检查证明是否有效，同时验证矿工的工作量证明是否满足要求。

2. 生成证明的调用流程

//Executes the instruction.
pub fn execute<A: circuit::Aleo<Network = N>>let response = substack.execute_function::<A, _>(call_stack, rng)?let proof = match proving_key.prove(function.name(), &assignment, rng) let proof = Proof::new(Marlin::<N>::prove_batchSelf::prove_batch_with_terminator(fs_parameters, proving_key, input_and_witness, &AtomicBool::new(false), rng)// First roundSonicKZG10::<E, FS>::commit// Second roundAHPForR1CS::<_, MM>::prover_second_round(&verifier_first_message, prover_state, zk_rng)// Third roundAHPForR1CS::<_, MM>::prover_third_round(&verifier_second_msg, prover_state, zk_rng)?let pc_proof = SonicKZG10::<E, FS>::open_combinations(

3. MSM（Multi-Scalar Multiplication）为约束产生证明

MSM 在 Aleo 挖矿中的 zkSNARK 证明生成中起着至关重要的作用。MSM 用于计算多个标量和椭圆曲线点的乘积累加，它被广泛用于生成 zkSNARK 证明的过程中，特别是在执行 Groth16、Marlin 等 zkSNARK 方案时。

以下是 MSM 在证明生成中的具体作用：

计算电路约束的加密承诺：
Aleo 的 zkSNARK 证明基于对电路中变量的加密承诺。每个变量会被映射到椭圆曲线上的一个点，MSM 通过对这些点和相关的标量进行乘法和累加来生成这些承诺。
- 电路中的每个变量被表示为一个标量 $s_i$ ，这些标量会与椭圆曲线点 $P_i$ 进行标量乘法，然后通过 MSM 将所有标量乘法的结果累加，生成最终的加密承诺： $\sum (s_i \cdot P_i)$ 这里， $s_i$ 是标量， $P_i$ 是椭圆曲线点，MSM 负责对它们进行乘积累加。
电路验证中的约束检查：
zkSNARK 证明生成的核心是证明某些约束是否在电路内成立，这需要将多个椭圆曲线点和标量相结合。MSM 用于计算这些点和标量之间的关系，并生成验证过程中所需的承诺点。
使用 Pippenger 优化 MSM (CPU)：
在 Aleo 的 zkSNARK 中，为了优化 MSM 的效率，通常会使用 Pippenger 算法，它可以将标量乘法和点累加并行化处理，并通过分组来降低计算复杂度。这对于生成 zkSNARK 证明至关重要，尤其是在大规模电路下，MSM 可以通过 Pippenger 优化算法显著提升性能。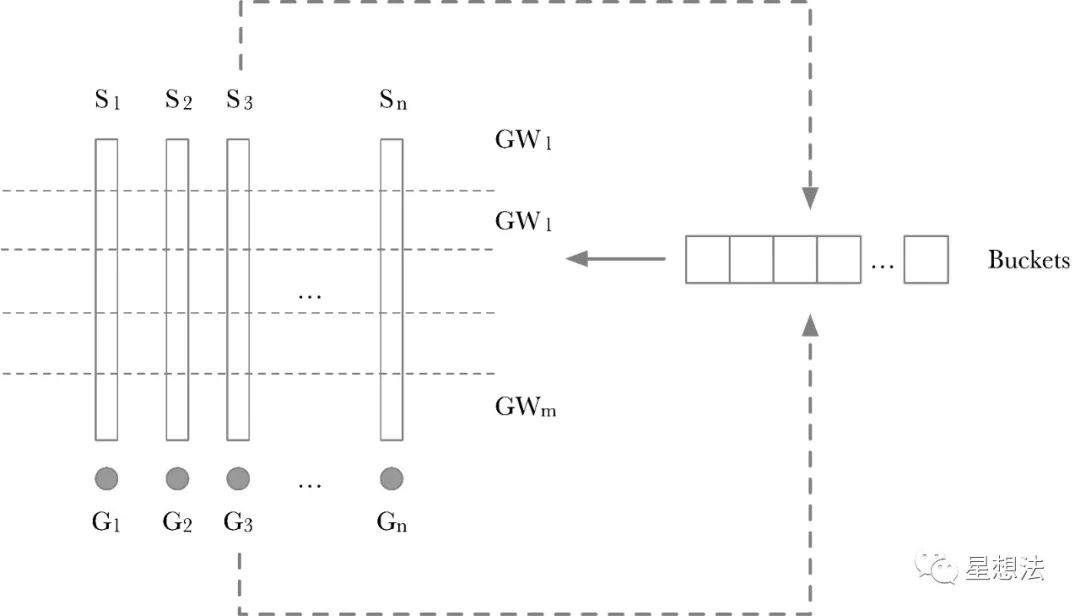
1. Scalar切分为Windows。如果Scalar是256bits，并且一个Window是8bits，则所有的Scalar切分为256/8=32个Window。每一层的Window，采用一个“Buckets”临时存放中间结果。 $GW_x$ 就是一层上的累加结果的点。计算 $GW_x$ 也比较简单，依次遍历一层中的每个Scalar，根据Scalar这层的值作为Index，将对应的 $G_x$ 加到相应的Buckets的位上。其实原理也比较简单，如果两个点加的系数相同，则先将两个点相加后再做一次Scalar加，而不需要两个点做两次Scalar加后再累加。
2. 每个Window计算出来的点，再通过double-add的方式进行累加，从而得到最后的结果。
1. 窗口分组：选择一个窗口大小 w（通常是一个可调参数），然后将每个标量 $a_i$ 的二进制表示分成若干 w 位的窗口。例如，将 $a_i$ 表示为若干 w 位块 $ja_{i,j}$ 。
2. 点预计算：对于每个窗口值，提前计算出对应的点乘值。这些点乘值可以通过少量的椭圆曲线加法和倍乘操作得到。
3. 分层累加：根据分好的窗口，将标量乘法分解为多个子部分，然后在这些子部分上进行批量点加操作。最终结果是通过合并各个窗口层的结果得到的。
4. 优化原理：由于窗口分解后，可以减少重复的标量乘法次数，并且可以将许多小的计算合并在一起批量执行，这样可以利用缓存和并行性来提升效率。
5. Pippenger算法的计算复杂度约为 $O(nw+2w)O(\frac{n}{w} + 2^w)$
还可使用桶算法（Bucket Method）优化MSM
使用Cuda并行计算MSM (GPU)

4. 规模

MSM的复杂度直接受到约束数量的影响, 对于一个带有 n 个约束的zk-SNARK电路，MSM的复杂度大约是 $\log n)$ 或 $O (n)$

✅ synthesize           (Constant: 2495, Public: 501, Private: 30624, Constraints: 31307, NonZeros: (72044, 62128, 41913))

猜测: 对于一个产生了 3 万个约束的 Aleo 程序，生成 zkSNARK 证明时，MSM 需要处理 3 万个基点和标量对。

UT

# snarkvm tag: v0.9.13fn test_fft_correctness()ntt logwcctest fft size
----------------------------------------------    
//[推荐]
fn prove_and_verify_with_large_matrix()//circuit/environment/src/helpers/converter.rs
fn test_marlin() 
fn marlin_snark_test()msm logwcctest cuda Number of baseswcctest cpu Number of baseswcctest cpu-Pippenger  Number of bases

估算:

函数:

//NTT
pub fn fft<T: DomainCoeff<F>>(&self, coeffs: &[T]) -> Vec<T> {
//fft 参数的数据类型和大小:
- coeffs:  `ScalarField, 32 bytes, 253 bits`#[inline(always)]fn butterfly_fn_oi<T: DomainCoeff<F>>(((lo, hi), root): ((&mut T, &mut T), &F)) {*hi *= *root;let neg = *lo - *hi;*lo += *hi;*hi = neg;}//MSM
pub fn msm<G: AffineCurve>(bases: &[G], scalars: &[<G::ScalarField as PrimeField>::BigInteger]) 
//MSM 参数的数据类型和大小:
- bases: `AffineCurve, 104 bytes`
- scalars:  `ScalarField, 32 bytes, 253 bits`

Constraints	NTT size	NTT coeffs len	NTT参数总大小(MB)	NTT运算次数	MSM size	MSM bases len	MSM scalars len	MSM参数总大小 (MB)	MSM运算次数	MSM c	参数文件
8192 (1<<13)	$2^{16}$	16384	0.5	butterfly: 16	$2^{15}$	32768	32768	4.25	add: 85995 double: 252	12	15
16384 (1<<14)	$2^{17}$	65536	2	butterfly: 17	$2^{16}$	65536	65536	8.5	add: 155629 double: 247	13	16
32768 (1<<15) (常规epoch-含1个pow.w)	$2^{18}$	131072	4	butterfly: 18	$2^{16}$	65536	65536	8.5	add: 155629 double: 247	14	16
65536 (1<<16) (高难度epoch-含6个pow.w)	$2^{19}$	262144	8	butterfly: 19	$2^{17}$	131072	131072	17.0	add: 155629 double: 247	15	17

https://testnet3.parameters.aleo.org/powers-of-beta-16.usrs.84631bc

panicked at circuit/environment/src/helpers/converter.rs:242:88:
called Result::unwrap() on an Err value: Crate(“marlin”, “PolynomialCommitmentError(AnyhowError(curl::error: Error { description: “Couldn’t resolve host name”, code: 6, extra: Some(“Could not resolve host: testnet3.parameters.aleo.org”) }))”)

msm cpu 代码

pub fn msm<G: AffineCurve>(bases: &[G], scalars: &[<G::ScalarField as PrimeField>::BigInteger]) -> G::Projective {// Determine the bucket size `c` (chosen empirically).let c = match scalars.len() < 32 {true => 1,false => crate::msm::ln_without_floats(scalars.len()) + 2,};let num_bits = <G::ScalarField as PrimeField>::size_in_bits();// Each window is of size `c`.// We divide up the bits 0..num_bits into windows of size `c`, and// in parallel process each such window.let window_sums: Vec<_> =cfg_into_iter!(0..num_bits).step_by(c).map(|w_start| standard_window(bases, scalars, w_start, c)).collect();// We store the sum for the lowest window.let (lowest, window_sums) = window_sums.split_first().unwrap();// We're traversing windows from high to low.window_sums.iter().rev().fold(G::Projective::zero(), |mut total, (sum_i, window_size)| {total += sum_i;for _ in 0..*window_size {total.double_in_place();}total}) + lowest.0
}