整数规划经典问题类型

BIP with additional constraints

Constraints

If investment 2 is made, then investment 4 must also be made：
it means: if $x_2=1$ then $x_4=1$
$$x_2\le x_4$$

If investment 1 is made, then investment 3 cannot be made,
it means: if $x_1=1$ then $x_3=0$
$$x_1+x_3\le 1$$

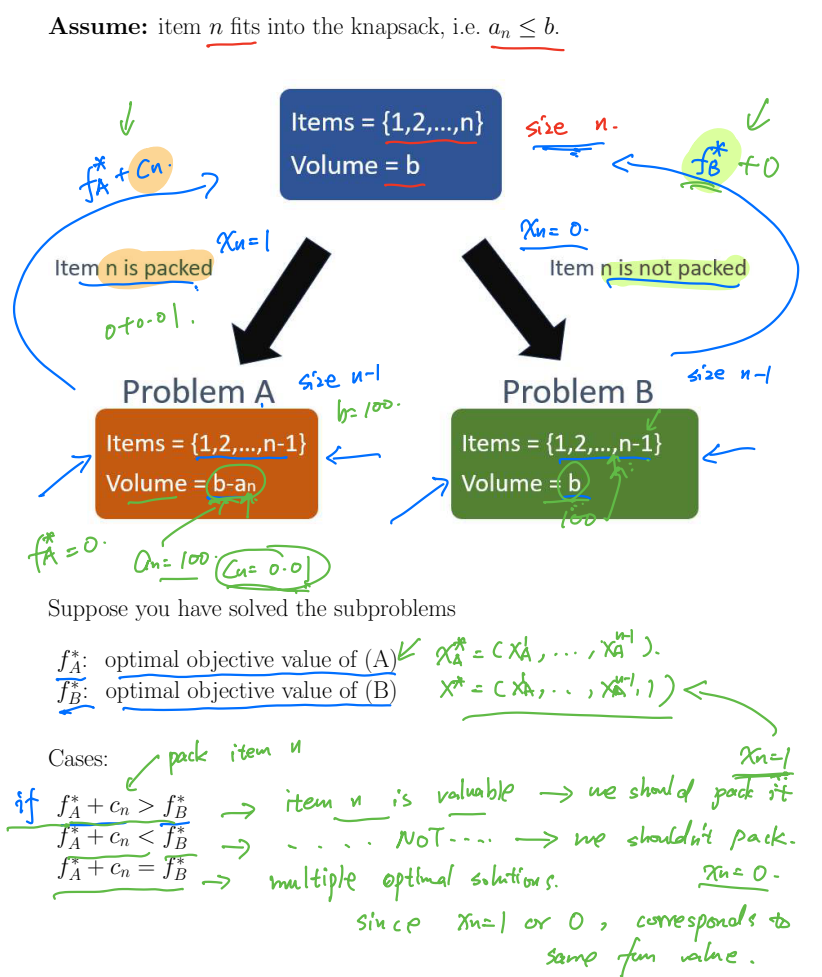
0-1 Knapsack Problem

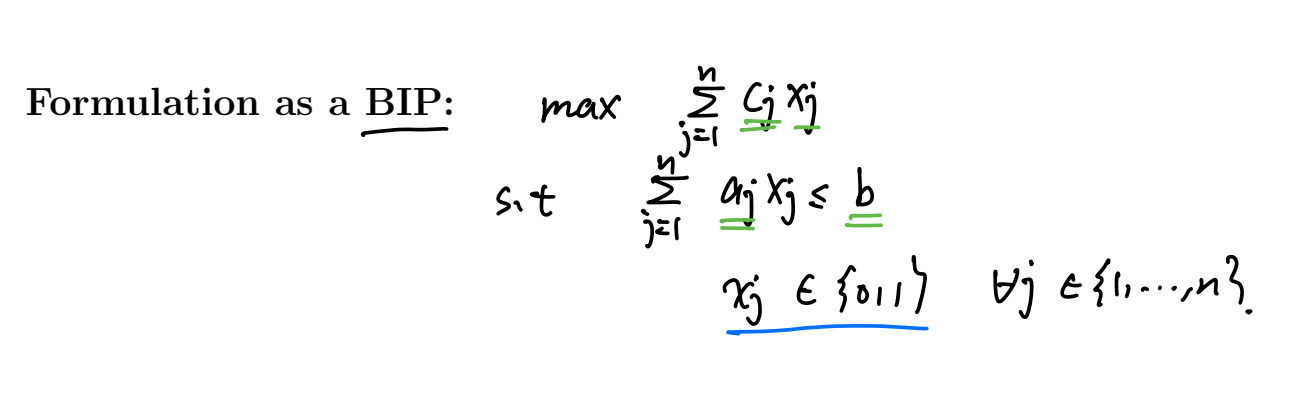
Integer Knapsack Problem

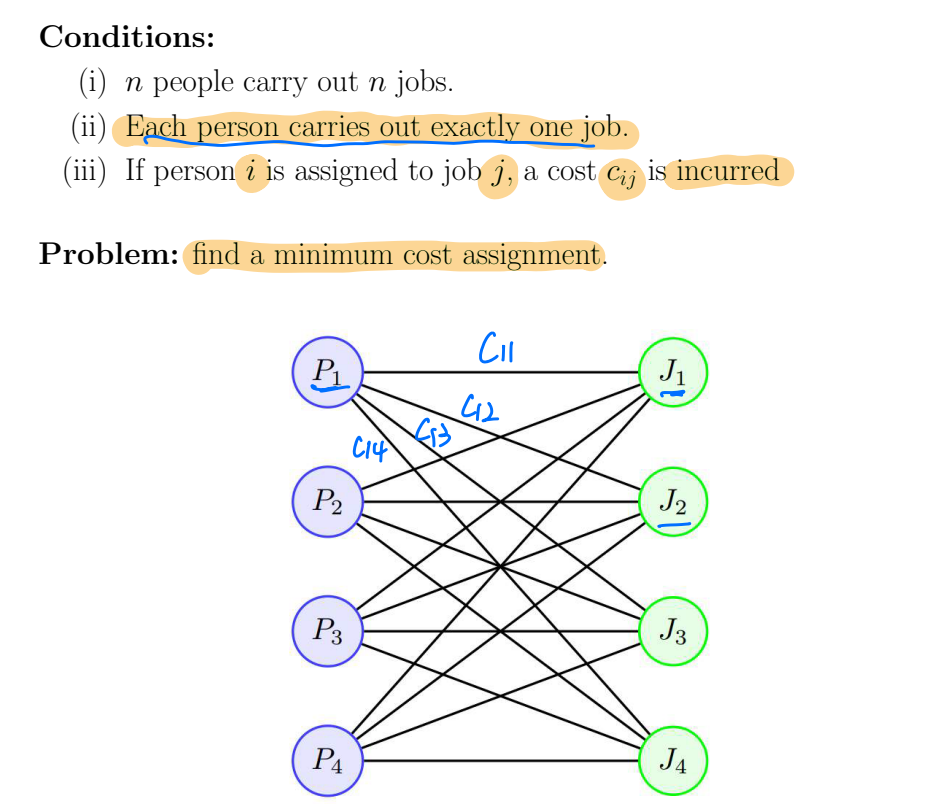
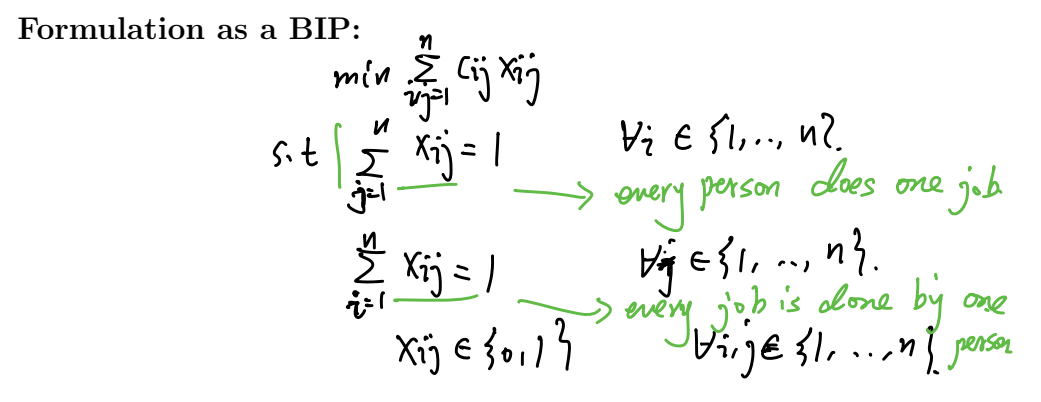
Assignment problem

Set covering problem

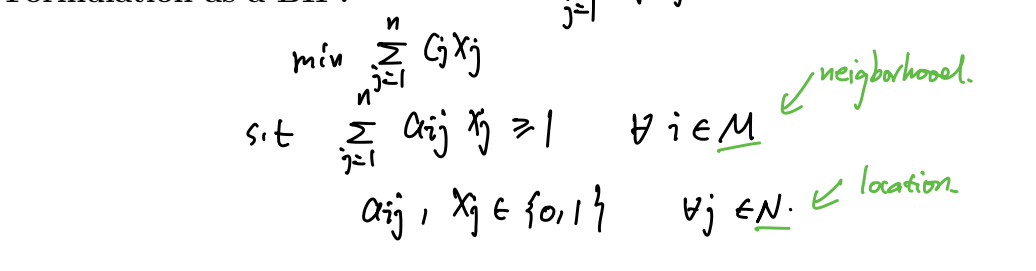
注意这里是任意i和任意j都满足。

Traveling salesman problem

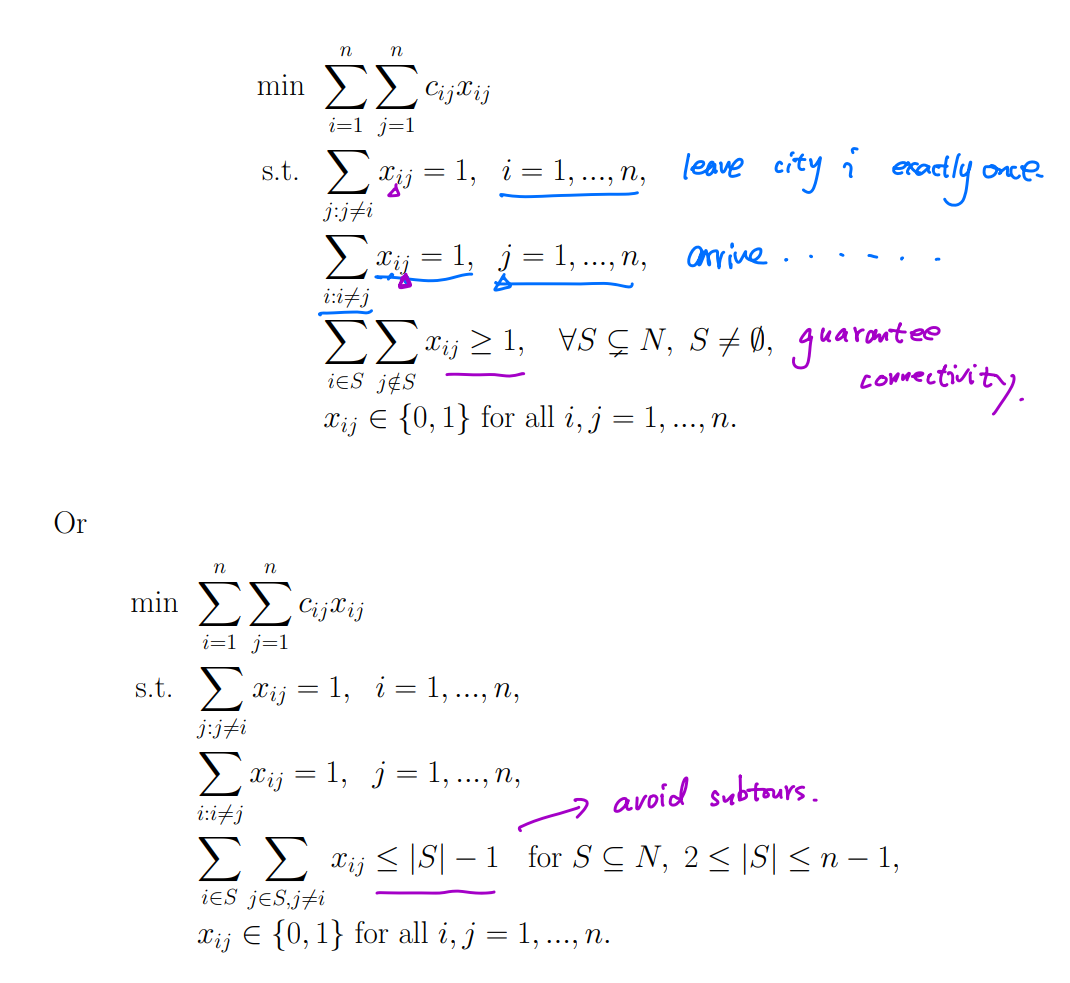
注意：因为我们并不知道在求解时，哪个子集 S 会形成独立的小圈(subtour)。
为了防止任何这种情况出现， 我们必须“对所有可能的 S”都强制加上限制条件。

Brute Force

The Knapsack and Covering Problems

设 ($b=\frac{1}{2}{\sum }_{i=1}^n{a}_i$) 是一个人为构造的假设场景

这是一个特殊例子，不是背包问题的通式，而是为了说明：

意思是：
背包容量刚好等于所有物品总体积的一半。

这样做的好处是——一半一半的结构很对称、便于证明：

对任意子集 (S)，它与其补集 ($S^c$) 的总体积一正一反，刚好在 (b) 的两边。

---

补集关系推导（关键逻辑）

写出体积总和：

${\sum }_{i=1}^n{a}_i={\sum }_{i\in S}{a}_i+{\sum }_{i\in S^c}{a}_i=2b.$

于是得到：
$$\text{若 }\sum _{i\in S}{a}_i>b,\text{ 则 }\sum _{i\in S^c}{a}_i<b.$$

$$\text{若 }\sum _{i\in S}{a}_i<b,\text{ 则 }\sum _{i\in S^c}{a}_i>b.$$

这说明：

对任意一个子集 (S)，要么它满足背包约束（可行），要么它的补集 (S^c) 满足约束（不可行）。

所以每一对子集 (($S$,$S^c$)) 至少有一个是可行的。
这就建立了“配对”思想。

三、由配对思想推出至少有 (2^{n-1}) 个可行解

我们知道所有子集共有 (2^n) 个。
如果把它们分成互补对子：
每对只算一次，总共有：
$$\frac{2^n}{2}=2^{n-1}$$
而每对中至少有一个满足约束 ($\sum a_i{x}_i\le b$)。
所以我们得到结论：
$\text{至少有 }{2}^{n-1}\text{ 个可行解。}$

Graphical method

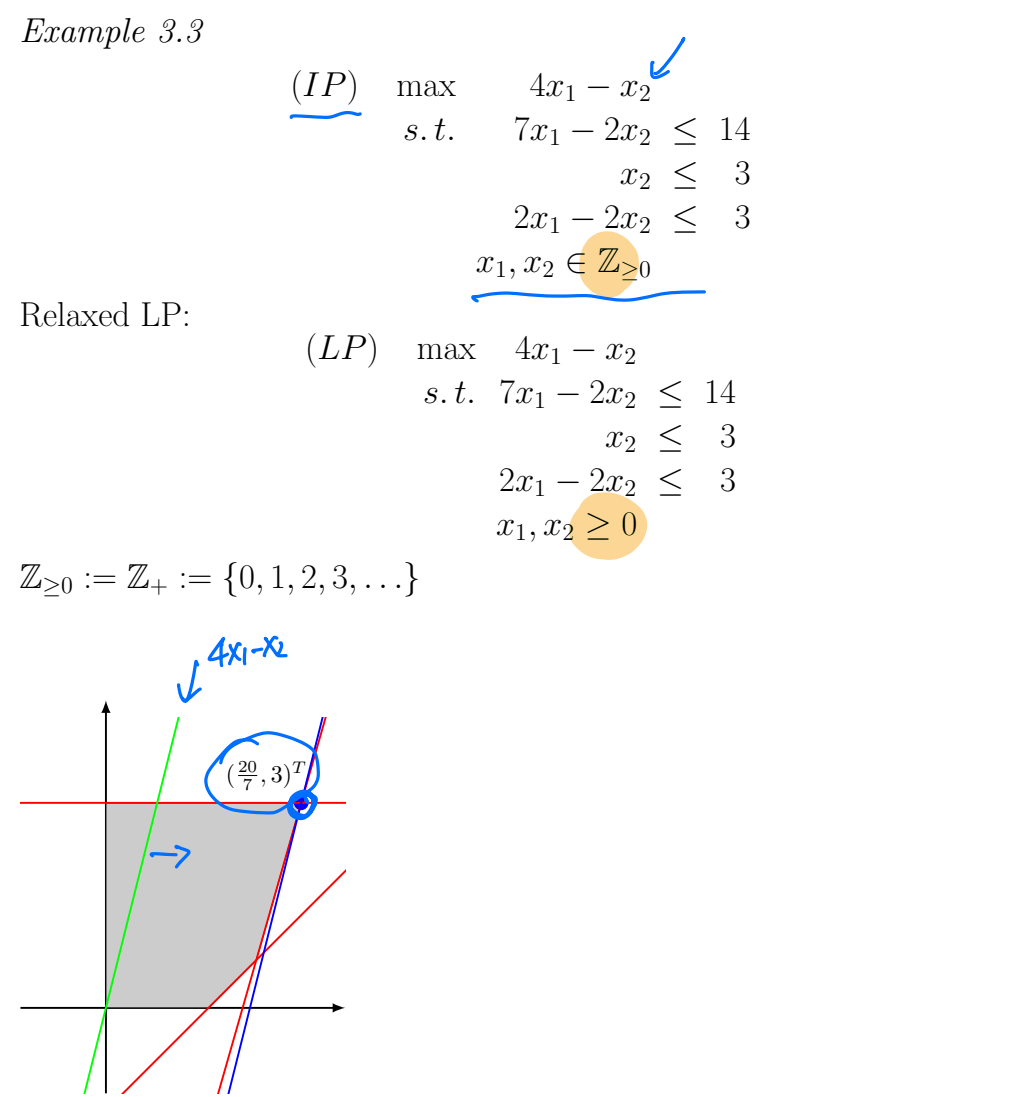
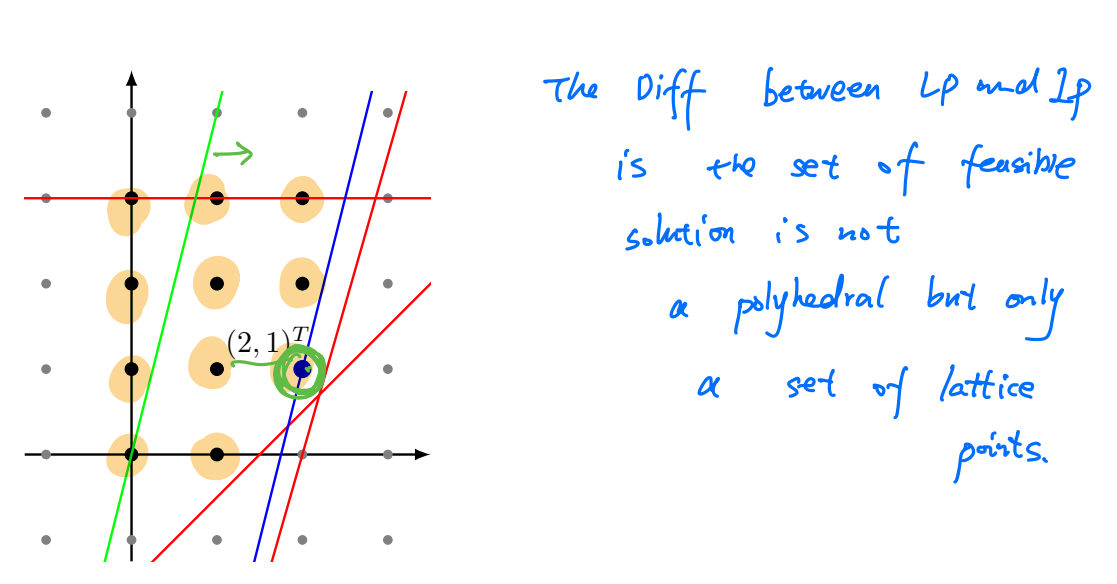
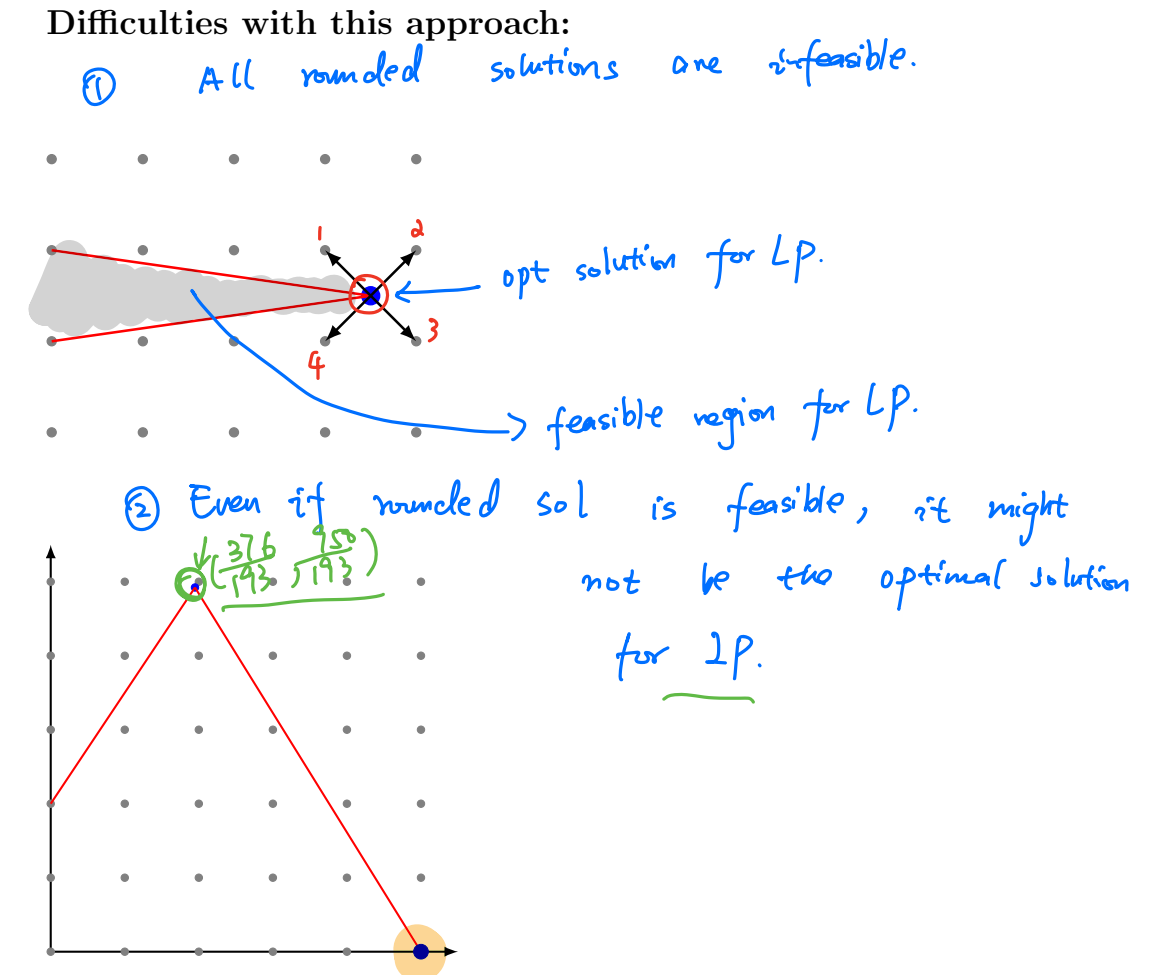
Divide and Conquer