频率在空间上的投射
究竟是周期还是频率，并不重要。因为频率需要周期，周期构成频率。另外若要标定一个周期中的特定相位，也需要相位之间具有可标定的差异，而只有不同的频率才能构成可标定的差异，才能给出相位以及相位差的有效信息，所以我们只考虑频率，因为频率提供更基本的度量能力。
既然说只需要频率，那么也就是只有一个变量，一个变量对应于一个维数，那么现实世界中的三个维数是怎么来的。或者稍微简化一些，两个维数是怎么来的。
具体来说，当我们平视前方，叫做仰角的角度为0，当我们仰天而望，这个仰角就是90°，或者
，或复平面上的
，如果角度再大一些呢？周期性就开始体现出来。换句话说，此时的仰角，就是某种极限。根据上面的分析，我们知道，能够实现精确度量的，就只有频率，那么对于角度来说，显然也是如此，也就是说我们可以建立角度和频率之间的对应关系。假定平视的时候仰角为0，对应于某个特定的频率
，那么仰天的时候，很自然的，我们只能选择虚数单位，这时候的频率就是，
继续转动角度，再次回到平视的状态，则表现为，
所以我们可以很自然的把物理世界中的角度和某种特定的频率或者频率范围对应起来。也就是说，完全可以只用复数的概念，就能描述物理实相中的仰角机制。我们这里要讨论的，就是这两者是如何对应的。
考虑复平面上的一个单位圆，
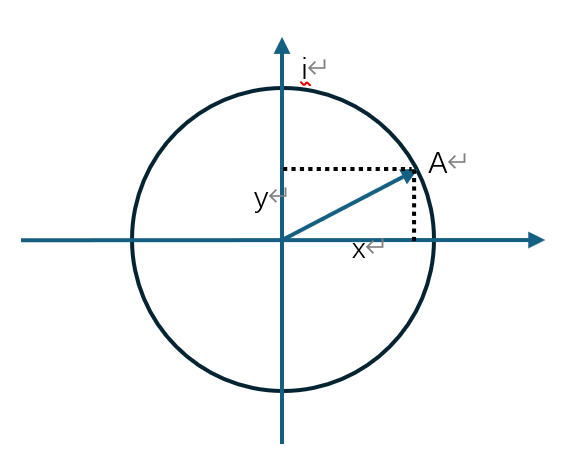
下面这个图像给出上面提到的对应关系，以下做具体分析。
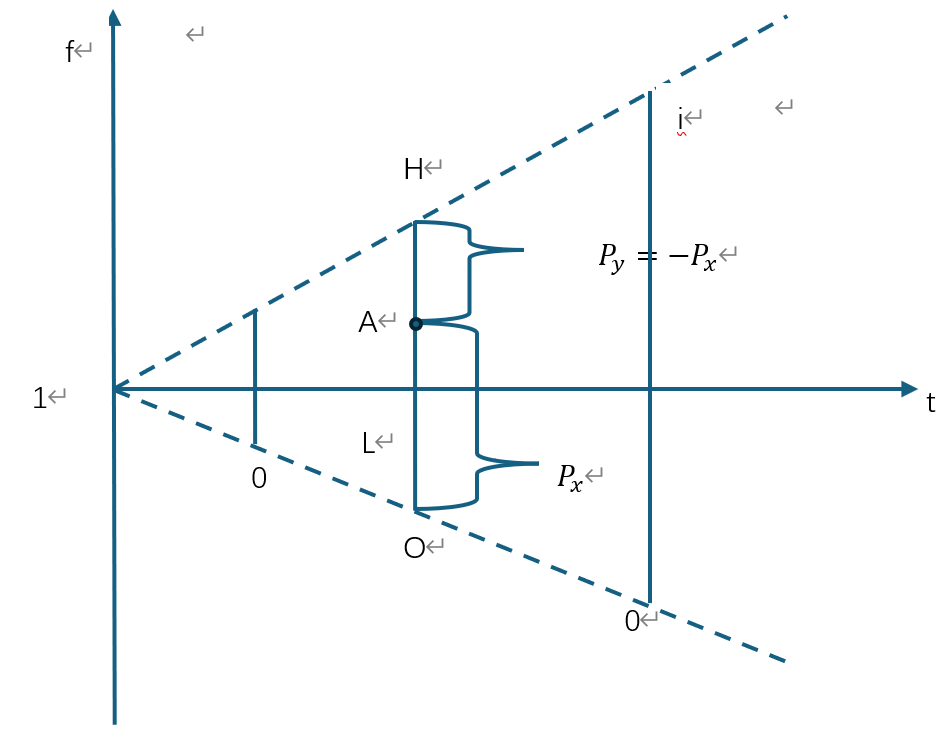
图像中横轴上每一点数值都是1（不是0），下面的射线上每一点的数值都是0，上面的射线每一点的数值都是不同数值的虚数单位。图像从左到右画出，角度张开的方向体现了0线不断下降，虚数单位逐渐增长的过程。严格来说，上面的射线符合，
下面并不是射线，而是符合，
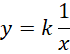
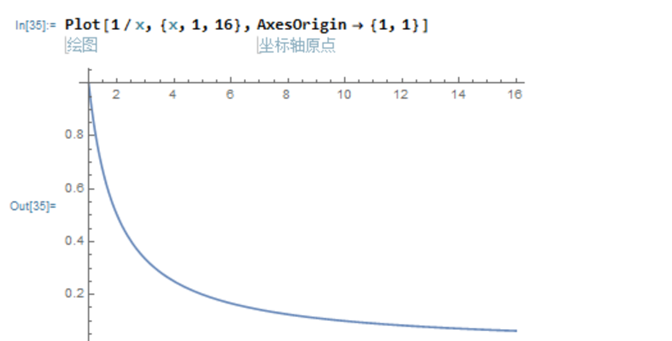
可以认为，在纵轴方向上两点之间的距离，就是虚数单位为特定值的复平面上的单位圆的半径，也就是虚数单位本身（并不是1）。这个图像给出了复平面上的一系列同心圆所对应的频率范围和关系。其特殊的地方就在于，纵轴的频率是有意义的，横轴只是把不同的频率投射在同一个图像里面，所以横轴的单位只能是纯数，作为不同大小的虚数单位的陈列下标。但是，若考虑到虚数单位本身具有自增的性质，那么横轴就可以被理解为对应于自增过程的时间，也就是说，它可以作为无量纲的时间轴存在。
考虑在OLAH 线上的频率上升的过程，从基点频率 
上升到 
到 
到 
。已知 
为频率0点，但是我们知道这只是相对频率0点，它的频率必然不为0（频率为0的振动周期为无穷大）。L点频率 
，A点频率未知设为 
，H点频率 
，由此可以认为， 
。这也是我们把L画成水平的基线的原因。因为这里的0的本质只是小于 
的频率。
现在考虑用，
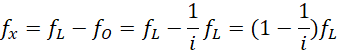
两种度量系统来度量A点的频率 
，
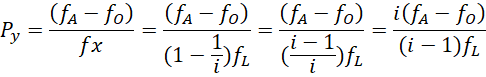
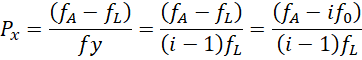
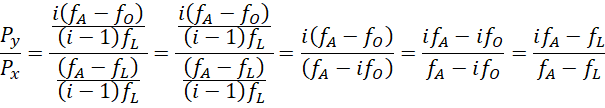
因为 
被认为是倍率的基点，在这个系统中我们将它视为0，
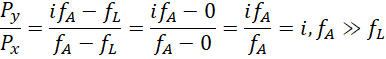
可见 
和 
对于任意，
都是互相垂直的。由此来说， 
和 
就可以认为是 
或者 
的纵坐标和横坐标。
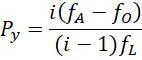
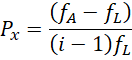
将两者等比放大 
倍，
再把 
缩小 
倍，
这里需要说明的是，缩小虚数单位倍，说明我们现在是在处理内部系统，就像先前说的用大整数表示高精度纯小数的做法。对应于复平面，显然它就对应于0到1之间的数值，所以这个度量实际上是横坐标的度量方式。所以下面涉及的所有的x和y都应该调换过来。这也意味着，横轴实际上是从周期到0倒着度量的，纵轴才是从0到周期正着度量的（这一点从余弦和正弦函数的图像上也可以看出来）。
继续看另一个坐标，
可见，这时候，
从频率中可以看出，若从H向着O的方向反向度量，则有同一个种频差的两种相反表示，
所以，
将其放大 
倍，
同时，
两者相乘，
此时若认为，
则有，
保持，
则平方和，
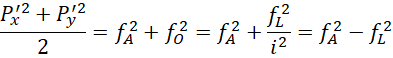
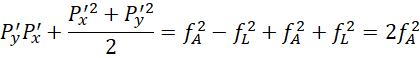
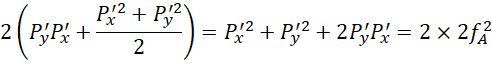
假定正值开平方，
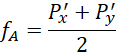
也就是说，如果Px'
和Py'
分别就是在两个轴上投射的横纵坐标，那么实际频率fA
就是这两个坐标的数值之和的一半，至少在第一象限是这样的。把这个情况代回单位圆，
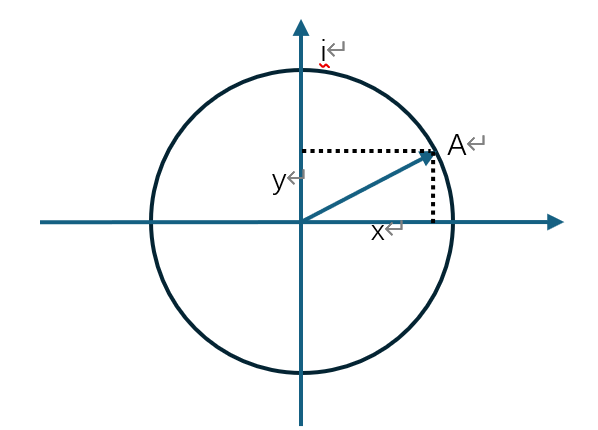
在我们保证，
的时候，其实 
是震荡变化的，
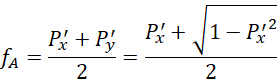
完整图像如下，
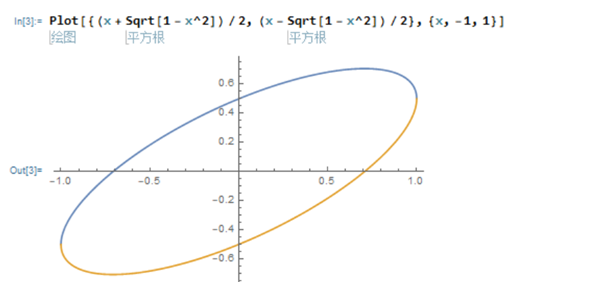
让我们考虑其它情况，
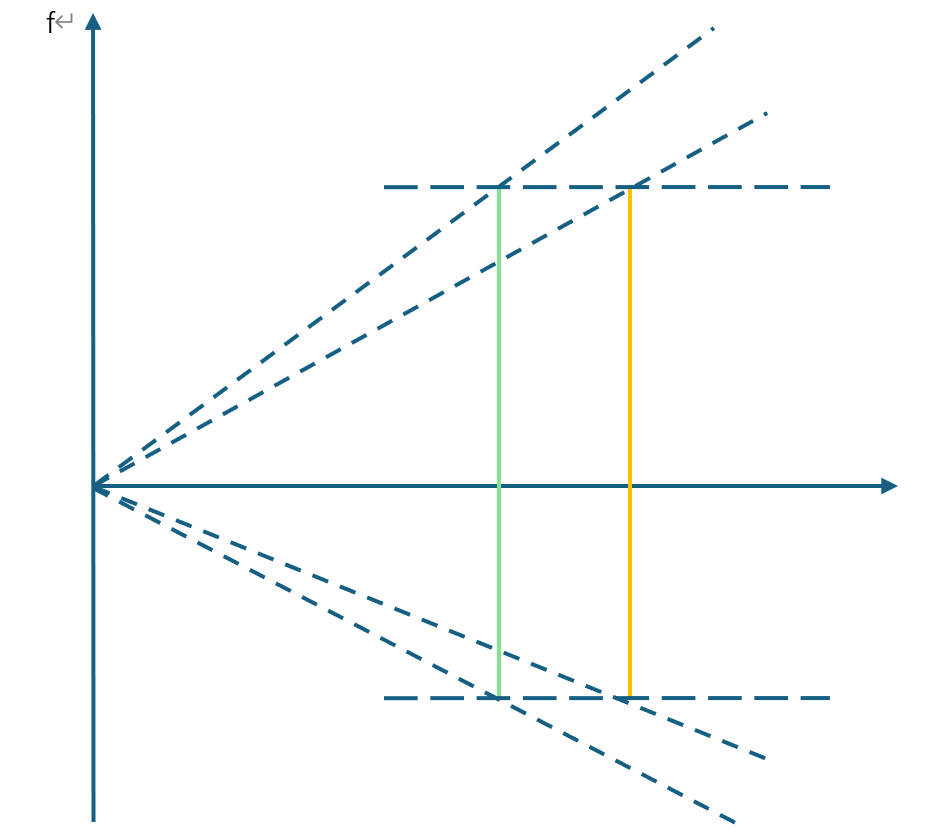
既然在横轴特定点上对应的纵轴上的长度，意味着虚数单位i
的大小，那么由这些虚数单位和其倒数的频点构成的张角的大小本身就意味着虚数单位随着时间增长而增长的速率（快慢）。进而可以推导出，不同的张角就意味着不同的增长速率。张角越大，虚数单位随着时间增长的速率越大，同样的时间间隔，张角大的虚数单位的数量增长更多。这也意味着，在时间的方向上，张角较大的，会更早扩展到张角小的对应的虚数单位将会扩展到的范围：图中的绿线在时间方向上先于橙线出现。当然这也意味着，时间轴上的过去现在和未来都是同时存在的。