patchmatch翻译总结

问题：在图像B中找到图像A中每个patch（像素块）的最邻近（最相似）patch。

近似最近邻算法

我们系统的核心是计算区块(patch)对应关系的算法。我们将最近邻域（NNF）定义为偏移量的函数 f : A ↦ R²，该函数基于所有可能的区块坐标（即区块中心位置）定义在图像 A 上，并依据两个区块间的某种距离函数 D。给定图像 A 中的区块坐标 a 及其在图像 B 中对应的最近邻 b，f(a) 即为 b - a。我们将 f 的值称为偏移量，这些值存储在一个维度与 A 相同的数组中。

本节提出一种用于计算近似 NNF 的随机算法。需要强调的是，推动该算法发展的关键思路在于：我们在可能的偏移量空间中进行搜索，相邻偏移量会协同搜索，并且对于大尺寸图像中的许多区块而言，即便是随机偏移量也很有可能成为良好的初始猜测。（这里是算法的核心思想：1相邻patch具有相似的特征并且其图A相邻patch的在图B中的近邻距离相近；2对于随机初始化近邻距离，利用传播也可以得到一个良好的结果）

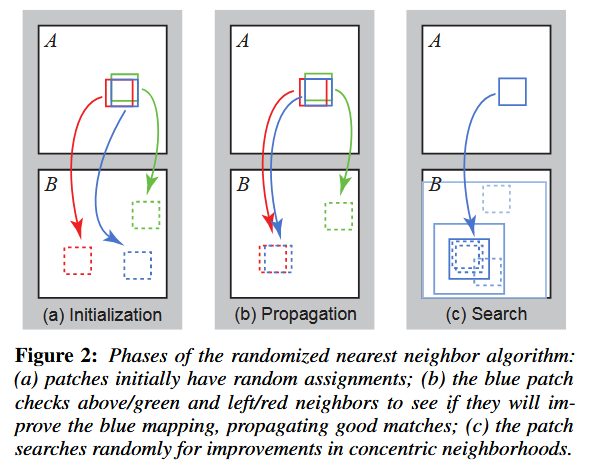
如图 2 所示，该算法包含三个主要组成部分。首先，最近邻域会以随机偏移量或某些先验信息进行初始化填充。随后对 NNF 实施迭代更新流程：将优质的区块偏移量传播至相邻像素，继而在当前最优偏移量邻域内进行随机搜索。第 3.1 节与 3.2 节将详细阐述这些步骤。

1 初始化

最近邻域（NNF）的初始化可通过两种方式实现：为字段分配随机值，或利用先验信息。采用随机偏移量初始化时，我们使用图像B全域范围内的独立均匀采样样本。

2 迭代

在初始化之后，我们执行一个迭代过程来改进最近邻域。算法的每次迭代按如下步骤进行：

按照扫描顺序（从左到右，从上到下）检查每个偏移量，并对每一个依次执行传播操作和随机搜索操作。这些操作在区块级别上是交错进行的：如果 Pj 和 Sj 分别表示对区块 j 的传播和随机搜索，那么执行顺序为：P1, S1, P2, S2, …, Pn, Sn。

传播
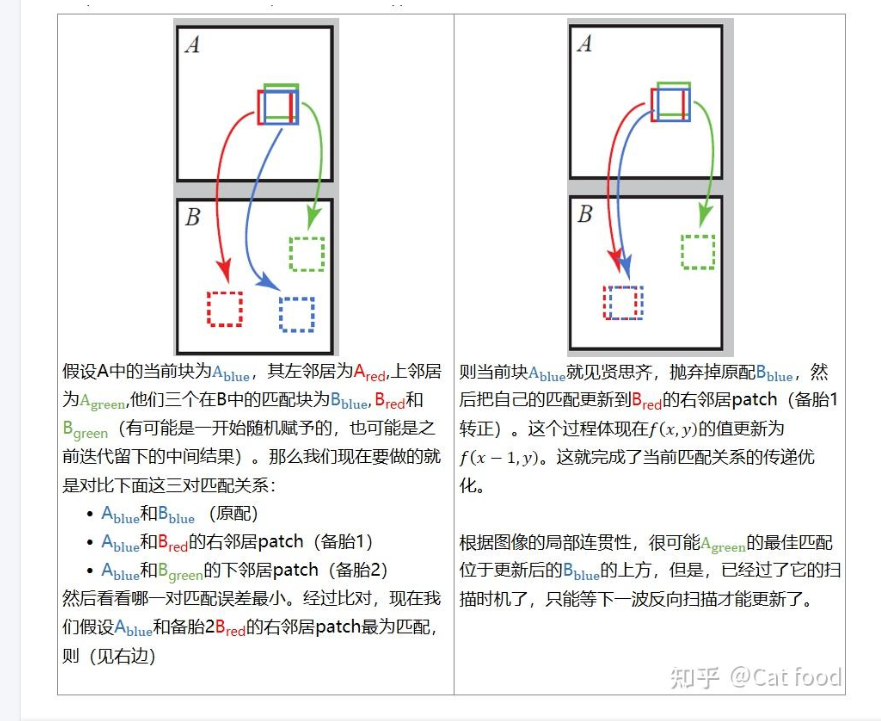
我们尝试利用 f(x-1, y) 和 f(x, y-1) 的已知偏移量来改进 f(x, y)，这基于一个假设：相邻区块的偏移量很可能是相似的。例如，如果在 (x-1, y) 处存在一个良好的映射，我们会尝试将该映射向右平移一个像素，作为 (x, y) 处的候选映射。令 D(v)（D(v)是一个度量函数但是文章并未指明具体公式） 表示图像 A 中 (x, y) 处的区块与图像 B 中 (x, y)+v 处的区块之间的距离（误差）。我们将 f(x, y) 的新值取为 {D(f(x,y)), D(f(x-1,y)), D(f(x,y-1))} 中能使误差最小的那个偏移量。

这样做的效果是，如果 (x, y) 处有一个正确的映射并且处于一个连贯区域 R 内，那么位于 (x, y) 下方和右侧的整个区域 R 都将被填入正确的映射。此外，在偶数次迭代中，我们会通过反向扫描顺序（从右到左，从下到上）检查偏移量，以向上和向左传播信息，此时我们使用 f(x+1, y) 和 f(x, y+1) 作为候选偏移量。

随机搜索

在进行传播之后还可能陷入局部最优，因此进行随机搜索。
令 v0 = f(x, y)。我们尝试通过测试一系列候选偏移量来改进 f(x, y)，这些候选偏移量到 v0 的距离呈指数级递减：
$ui=v_0+w{\alpha }^i{R}_i$
其中 R_i 是在 [-1,1] × [-1,1] 范围内的均匀随机向量，w 是一个较大的最大搜索"半径"，α 是搜索窗口大小之间的固定比率。我们依次检查 i = 0, 1, 2, … 对应的候选区块，直到当前的搜索半径 wα^i 小于 1 个像素。在我们的应用中，除非特别说明，w 是图像的最大维度（宽度或高度），且 α = 1/2。
需要注意的是，搜索窗口必须被限制在图像 B 的边界之内。

终止条件
虽然根据具体应用场景可以采用不同的迭代终止准则，但我们发现在实践中，采用固定迭代次数的方案效果良好。本文展示的所有结果均通过总计4-5次迭代计算得出，在此迭代次数后，最近邻域几乎总能达到收敛状态。图3及附带视频直观展示了收敛过程。

效率优化
这种基础算法的效率可通过以下几种方式提升：

1. 在传播和随机搜索阶段，当尝试用候选偏移量u来改进当前偏移量f(v)时，若计算D(u)的部分累加和已超过当前已知的最优距离D(f(v))，即可采用提前终止策略。

2. 在传播阶段，当处理边长为p的方形区块并使用Lq范数时，通过利用重叠区域求和运算中的冗余项，可将距离变化量的计算复杂度从O(p²)降至O§。但需要注意的是，这种优化需要额外分配内存空间来存储当前最优距离D(f(x,y))。

3收敛性证明

我们的迭代算法在极限情况下会收敛至精确的最近邻域。在此我们对该收敛过程进行理论分析，证明算法以高概率在前几次迭代中实现最快收敛。更重要的是，我们证明了在仅需获得近似区块匹配的常见应用场景中，算法的收敛速度会进一步提升。因此，通过将计算限制在少量迭代次数内，我们的算法能够作为最优的近似算法使用。

我们首先分析算法向精确最近邻域的收敛特性，随后将分析延伸至更具实用价值的近似解收敛情形。假设图像A与B具有相同尺寸（M个像素）且采用随机初始化。虽然单个位置在初始猜测中被分配最佳偏移量的概率极小（1/M），但至少有一个偏移量被正确分配的概率相当可观——其值为(1 − (1 − 1/M)^M)，对于较大的M约等于1 − 1/e。由于随机搜索在局部小范围内具有较高密度，我们也可将"正确"分配定义为：在正确偏移量周围C像素邻域内的任何分配。此类偏移量约经过一次随机搜索迭代即可被修正，而至少有一个偏移量落入此类邻域的概率极为显著：其值为(1 − (1 − C/M)^M)，对于较大M约等于1 − exp(−C)。

解释：

1. 至少一个偏移量被“精确”猜中的概率

原句：

“至少有一个偏移量被正确分配的概率相当可观——其值为(1 − (1 − 1/M)^M)，对于较大的M约等于1 − 1/e”

解释：

• 场景：我们有两张都是 M 个像素的图像 A 和 B。初始化时，对于 A 中的每一个像素点，我们都从 B 中随机地挑选一个像素点作为它的对应点（即随机分配一个偏移量）。

• “头奖”：我们关心的是，在所有这些随机的猜测中，至少有一个猜测是完全正确的概率有多大？所谓“完全正确”，就是指 A 中的某个点 a，恰好被分配给了它在 B 中真正的、最匹配的对应点 b。

• 计算过程：

  1. 对于某一次具体的猜测，它猜中“头奖”的概率是 1/M。那么它猜错的概率就是 (1 - 1/M)。

  2. 我们一共进行 M 次独立的猜测（因为图像有 M 个像素，每个像素都猜一次）。

  3. 所有 M 次猜测全都猜错的概率是：(1 - 1/M) * (1 - 1/M) * ... * (1 - 1/M) = (1 - 1/M)^M。

  4. 所以，至少有一次猜对（即不是全错）的概率就是：1 - (1 - 1/M)^M。

• 极限近似：
  当图像尺寸 M 非常大时（这是一个符合现实的假设，例如一张100万像素的图片，M=1,000,000），(1 - 1/M)^M 这个表达式趋近于自然常数 e 的倒数，即 1/e。
  因此，概率 1 - (1 - 1/M)^M 就趋近于 1 - 1/e。

• 数值理解：
  1 - 1/e ≈ 1 - 0.3679 ≈ 0.632 = 63.2%。
  结论就是：即使在最随机的初始化状态下，也有超过63%的概率至少有一个像素点被分配到了它绝对正确的对应点。 这个概率是相当可观的，它为后续的算法传播提供了“火种”。

---

2. 至少一个偏移量被“近似”猜中的概率

原句：

“至少有一个偏移量落入此类邻域的概率极为显著：其值为(1 − (1 − C/M)^M)，对于较大M约等于1 − exp(−C)”

解释：

• 放松标准：在实际情况中，我们不需要猜得“分毫不差”。只要猜到的点落在正确点周围的一个小邻域patch（假设这个邻域包含 C 个像素）内，我们就认为这是一个“近似正确”的、足够好的猜测。在后续的随机搜索中，算法可以很快地从这个小邻域中找到精确解。

• 计算过程：

  1. 对于某一次猜测，它落入这个“正确邻域”的概率变成了 C/M（因为有利区域从1个像素变成了C个像素）。

  2. 那么，一次猜测没有落入这个邻域的概率是 (1 - C/M)。

  3. 所有 M 次猜测全都未落入邻域的概率是：(1 - C/M)^M。

  4. 所以，至少有一次猜测落入邻域的概率是：1 - (1 - C/M)^M。

• 极限近似：
  当 M 很大时，(1 - C/M)^M 趋近于 exp(-C)。
  因此，概率 1 - (1 - C/M)^M 就趋近于 1 - exp(-C)。

• 数值理解与结论：
  这个概率 1 - exp(-C) 的大小完全由邻域大小 C 决定。C 不需要很大，这个概率就会变得非常高。

  • 如果 C = 3，概率 ≈ 1 - exp(-3) ≈ 1 - 0.05 ≈ 95%

  • 如果 C = 5，概率 ≈ 1 - exp(-5) ≈ 1 - 0.007 ≈ 99.3%
    结论就是：只要我们把“正确”的标准放宽到一个很小的邻域内，那么在初始化阶段就获得至少一个“近似正确”匹配的概率几乎是必然的（接近100%）。

总结

PatchMatch是一种随机搜索算法，用于高效计算两幅图像之间密集的近似最近邻域。它的革命性在于，它通过巧妙的随机性和传播机制，在巨大的搜索空间中以极小的计算量获得高质量的结果，其速度比传统的暴力搜索快数个数量级。

---

一、核心思想

算法建立在三个关键洞见之上：

1. 在偏移量空间搜索：不直接搜索匹配的像素块，而是搜索连接它们的偏移向量。这个偏移量场就是最近邻域。

2. 空间一致性：自然图像中，相邻的像素块通常具有相似的偏移量。因此，好的偏移量可以传播给它的邻居（最核心思想）。

3. 随机性的力量：即使在巨大的图像中，一个随机的偏移量也有很高的概率是某些像素块的“还不错”的猜测，这为算法提供了优化的起点。

二、算法工作流程

算法通过一个迭代过程来不断优化偏移量场，每次迭代包含两个核心步骤：

1. 初始化

• 将最近邻域用随机偏移量进行填充。虽然单个随机偏移量质量很差，但根据概率分析，在整个图像范围内，至少会有一些偏移量碰巧落在正确解的附近，这为后续迭代提供了“火种”。

2. 迭代优化 每个像素点会依次经历以下两个阶段：

• 传播 - 利用空间一致性

  • 目的：将邻近像素已找到的好偏移量传递过来。

  • 操作：检查当前像素左边和上边（在偶数次迭代时则为右边和下边）像素所使用的偏移量。将当前像素的偏移量与这些“邻居”的偏移量进行比较，选择其中能使得图像块差异最小的那个。

  • 效果：像一个“好主意”在图像中蔓延。一旦某个区域找到一个正确偏移量，它会迅速像波浪一样传播到整个连续区域。

• 随机搜索 - 避免局部最优

  • 目的：在当前位置附近进行精细搜索，并保留跳出局部最优解的可能性。

  • 操作：以当前最佳偏移量为中心，在一个初始较大但指数级缩小的窗口内进行随机采样。公式为 ($u_i=v_0+w{\alpha }^i{R}_i$ )。

  • 效果：首先在较大范围内寻找可能更好的解，然后逐步收拢进行精细调整。这种策略平衡了“探索”和“利用”。

三、关键优势与特性

1. 极高的效率：通过传播和随机搜索，避免了暴力搜索 (O(N^2)) 的复杂度，通常仅需 4-5次迭代 即可收敛。

2. 易于实现：算法框架清晰，核心代码非常简洁。

3. 理论保证：概率分析证明，即使从随机状态开始，算法也能以极高的概率快速收敛到一个良好的近似解。

4. 灵活性：可以与金字塔 coarse-to-fine 策略结合，进一步提升性能和稳定性；也可以融入各种先验信息来初始化。

四、主要应用场景

PatchMatch的核心是寻找密集对应关系，因此其应用非常广泛，包括：

• 图像编辑：

  • 图像补全/修复：从图像的其他部分复制纹理来填充缺失区域。

  • 重排：重新排列图像中的物体。

• 纹理合成：根据样本纹理生成大尺寸的无缝纹理。

• 立体视觉与深度估计：为左右视图的像素寻找对应点，从而计算深度。

• 图像超分辨率：从低分辨率图像中找到高分辨率的细节块。

• 视频处理：应用于视频稳定、补全等。

五、总结

PatchMatch算法的精髓在于 “随机初始化提供火种，近邻传播步骤形成燎原之势，随机搜索步骤则负责局部精炼和突破”。它将计算机科学中经典的“随机化”与“局部搜索”思想相结合，以一种极其巧妙的方式解决了高维空间中的密集匹配问题，成为了计算机视觉和图形学领域一个里程碑式的算法。

参考：

解读PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing
Cat food的文章 - 知乎:
https://zhuanlan.zhihu.com/p/377230002