当前位置：首页 > news >正文

【CF】Day148——Codeforces Round 1057 (Div. 2) CD (非退化凸多边形的分类讨论 | 破环成链动态规划)

news 2025/10/12 7:40:34

C. Symmetrical Polygons

题目：

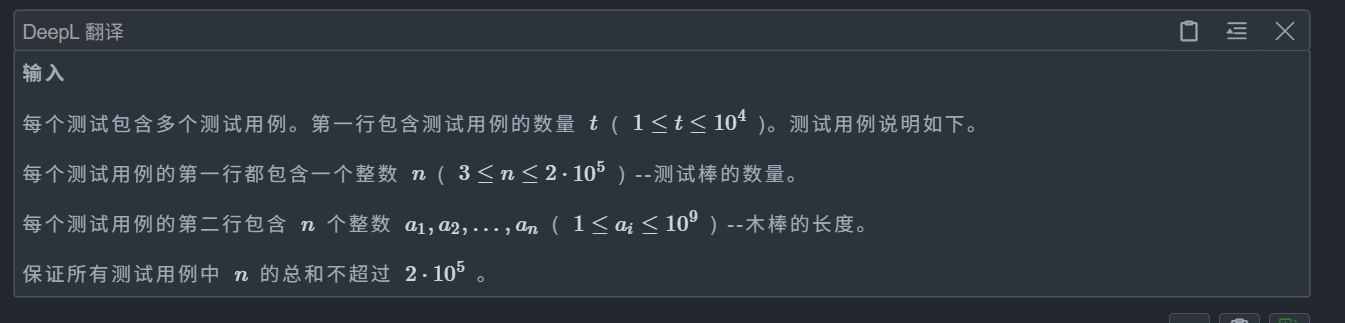
思路：

非退化

我们本题不难看我们可以选取所有的偶数边，同时对于奇数边我们可以选取 x - 1 条变成偶数条边

那么最后的关键点就是能否再选边？这是显然的，我们最多还能再选两条单边

所以分类讨论

①.选一条单边

那么就有这条单边必须小于其余边长之和

②.选两条单边

同上，但是我们只需要考虑较长边

③.不额外选

此时我们只需要判断任意一条边是否大于其余边之和即可

具体实现看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937_64 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n;cin >> n;vector<int> a(n + 1);map<int, int> mp;for (int i = 1; i <= n; i++){cin >> a[i];mp[a[i]]++;}int base = 0;vector<int> odd, even;for (auto &[val, cnt] : mp){base += val * (cnt / 2);if (cnt & 1)odd.push_back(val);elseeven.push_back(val);}if (base == 0){cout << "0\n";return;}int ans = 0;for (auto &x : odd){//总长 > 最长单边if (base * 2 > x){ans = max(ans, 2 * base + x);}}for (int i = 1; i < odd.size(); i++){//总长 > 最长单边if (odd[i - 1] + 2 * base > odd[i]){ans = max(ans, 2 * base + odd[i] + odd[i - 1]);}}for (auto& x : even){//总长 > 最长单边（2*base - x > x => 2*base > 2*x => base > x）//但是感觉实际是判断是不是只有两条边，因为如果可以 base > x 恒成立if (base > x){ans = max(ans, 2 * base);}}cout << ans << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;cin >> t;while (t--){solve();}return 0;
}

D. Not Alone

题目：

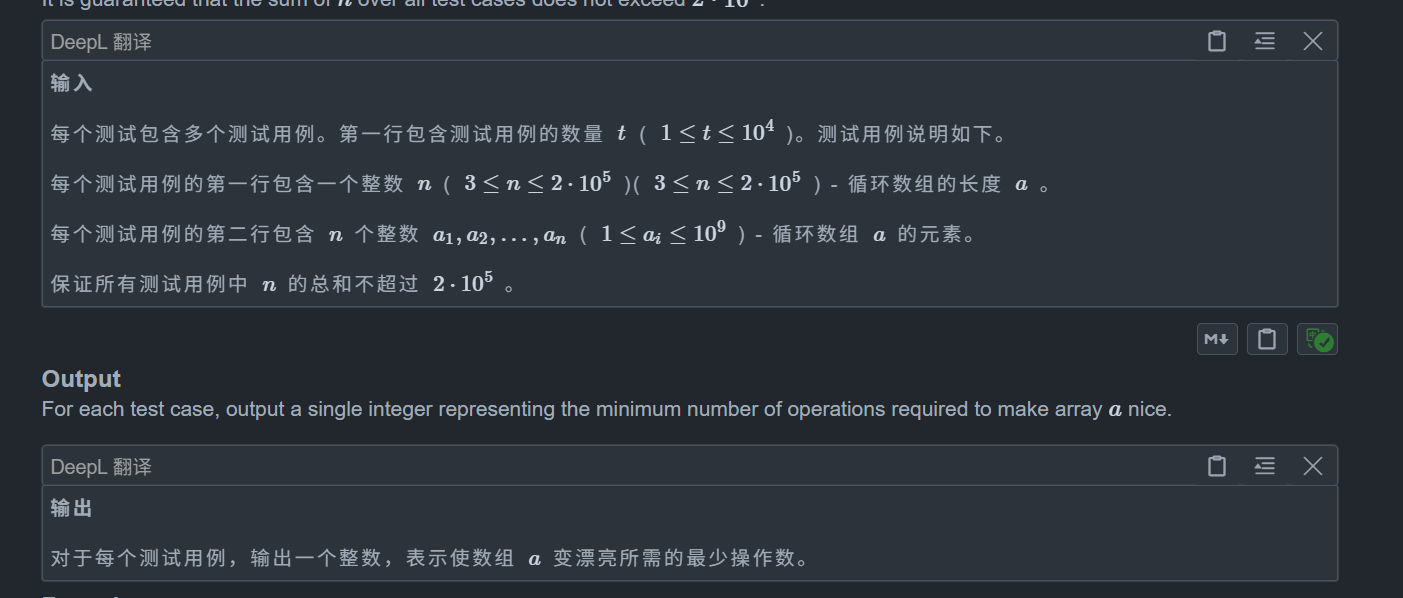思路：

经典性质

注意到对于该操作，假设最后有一段长为 len 的漂亮数组，那么其可以分割为 $2x+3y$ 的形式，即 x 个长 2 的数组 + y 个长为 3 的数组

证明：对于任意长 len 的漂亮数组（len > 3），我们可以取最后两个数，那么就有以下变化

$\sum_{i=1}^{len}|a[i] - x| \rightarrow \sum_{i=1}^{len-2}|a[i] - x| + |a[len] - a[len - 1]|$

可以发现原来最后两项的价值为 $|a[len]-x|+|a[len-1]-x|$ ，那么只有当 x 为最后两个数中的一个时，才有

$\sum_{i=1}^{len}|a[i] - x| = \sum_{i=1}^{len-2}|a[i] - x| + |a[len] - a[len - 1]|$

所以我们拿出最后两个数显然是不劣的

那么考虑dp，先考虑简单情况下如果没有环形这个条件如何转移

定义 dp[i] 为处理完前 i 个数的最小操作数，那么就有以下转移

$dp[i] = min(dp[i-2] + cost,dp[i-3] + cost)$

其中 cost 代表二块/三块的最小操作数，那么现在考虑环形

常见操作是破环成链，所以我们枚举破环的位置即可，但是由于本题的块的长度最多为 3，所以我们只需要多枚举 3 个破环点即可，即 $(1,2)(2,3)(3,4)$ 这几个点即可

但实际上只需要多枚举两个即可，即 $(1,2)(2,3)$ ，因为只有 $(n-1,n,1)(n,1)(n,1,2)$ 这几种组合方式是以 1 开头的情况下没考虑到的

具体的就是将数组全体往左平移一位即可，具体实现看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937_64 rnd(chrono::steady_clock::now().time_since_epoch().count());inline int cost(int x, int y) { return abs(x - y); }inline int cost(int x, int y, int z) { return max({x, y, z}) - min({x, y, z}); }void solve()
{int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i++){cin >> a[i];}int ans = 1e18;vector<int> dp(n + 1, 0);auto update = [&]() -> void{dp[0] = 0, dp[1] = 1e18;for (int i = 2; i <= n; i++){dp[i] = dp[i - 2] + cost(a[i - 1], a[i]);if (i >= 3)dp[i] = min(dp[i], dp[i - 3] + cost(a[i - 2], a[i - 1], a[i]));}ans = min(ans, dp[n]);};auto aswap = [&]() -> void{for (int i = 2; i <= n; i++)swap(a[i], a[i - 1]);};for (int i = 0; i < 3; i++){update();aswap();}cout << ans << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;cin >> t;while (t--){solve();}return 0;
}

查看全文

http://www.dtcms.com/a/469819.html