PID控制器的不同的传递函数与参数形式

 一、时域表达式

         PID控制器是基于经典控制理论的一种控制策略，其算法简单实用，PID控制并不要求受控对象的精准数学模型，这使得PID控制在工业生产过程中应用十分广泛。连续PID控制器的时域一般表达式为

        比例系数Kp、积分系数Ki和微分系数Kd分别是对系统误差信号e(t)及其积分与微分的加权系数。

        PID控制器通过对误差信号e(t)的加权计算，得到控制信号u(t)，驱动受控对象，使得误差e(t)按减少的方向变化，从而达到控制要求。

        在线性定常系统中，当初始条件为零时，系统输出拉氏变换与输入拉氏变换的比，称为传递函数，用G(S)表示。输入与输出之间的关系仅取决于电路的结构形式及其参数（固有特性）,与输入的具体形式无关，无论输入如何，系统都以相同的传递作用输出信息或能量，因此称之为传递函数。

二、复频域传递函数

        对上述公式做拉普拉斯变换，得到连续PID控制器的复频域传递函数

        Kp是比例系数，是积分时间常数，是微分时间常数。

        当Ti->，Td=0时，G(s)=Kp，为比例(P)控制器；

        当Td=0时，，为比例积分(PI)控制器；

        当Ti->时，G(s)=Kp(1+Tds)，为比例微分(PD)控制器。

三、近似传递函数

        为避免纯微分计算，常用一阶超前环节去近似纯微分环节，PID控制器的传递函数为

        式中，N->时，为纯微分运算。实际中，N不必过大，一般取N=10，就可以逼近实际的微分效果。在matlab的PID控制器中，N的默认值为100，值为上式中的N/Td=10/Td。

四、Matlab中PID控制器的传递函数

1、理想型补偿器公式

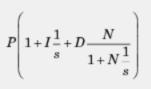
对于控制器参数整定来说，此时P=Kp，，。

2、并行型补偿器公式

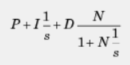
对于控制器参数整定来说，此时P=Kp，，。

五、结论

整定的时候，会计算出Ti，Td，有了这些换算关系，可以方便的算出Matlab中的P值、I值、D值，从而方便的进行仿真。