【神经网络】从逻辑回归到神经网络
- 对逻辑回归进行组合:顾客选购苹果预测
- 神经网络在层层转换过程中,究竟在试图实现什么?
对逻辑回归进行组合:顾客选购苹果预测
RethinkFun 深度学习
针对一个苹果,收集了以下特征,利用这些特征,希望预测用户购买并品尝这个苹果后是否满意。

另外,通过对大量顾客的跟踪访问,得到了测试样本的标签数据。

可以直接利用特征,通过逻辑回归模型来建模预测用户是否对一个苹果满意。但是有经验的销售人员告诉我们,顾客对苹果的满意是取决于以下三个因素:外观、口感、实惠。
于是,又额外再采集受访用户对一个苹果在上边三个因素上的评价。并 构造三个逻辑回归模型 来判断一个苹果在这三个因素上是否优秀。
外观 决定外观的因素有:果径,果高,果斑,包装。利用这四个特征训练一个逻辑回归模型,输出为 Sigmoid 的输出,取值范围为 0-1,代表外观是否美观。
口感 决定口感的因素有:甜度,酸度,水分,产地。利用这四个特征训练一个逻辑回归模型。
实惠 决定是否实惠的因素有:产地,重量,包装,售价。利用这四个特征训练一个逻辑回归模型。
最终,根据外观,口感,实惠的三个逻辑回归的输出值,再构建一个逻辑回归模型,判断用户是否对这个苹果满意。最终的系统由以下 4 个逻辑回归模型构成。

上边的顾客是否满意一个苹果的模型里,通过先验知识,抽象出来 3 个更高级的特征,那就是外观,口感和实惠。
对于这 3 个高级特征,
- 首先把它们作为要预测的目标,收集用户对这三个特性的评价 label。
- 然后 选择原始 feature,对这三个高级特征进行建模预测。
- 最后 利用这三个高级特征来预测最终目标,是否满意。
这样做有三个问题:
- 需要先验知识来构造高级特征,并且对于高级特征需要 人工筛选原始特征,这严重依赖于个人经验。
- 需要 额外采集高级特征的 Label 进行训练,增加了数据采集的工作量。
- 必须 先训练前三个抽象高级特征的模型,然后才能训练最后一个判断用户是否满意的模型。
对于上边的问题,可以做出如下的改进:
- 不人为抽象高级特征,让模型在训练过程中自己抽象高级特征。
- 将所有的原始特征接入到每个提取高级特征的逻辑回归模型,让模型学习使用哪些特征,模型可以通过训练将不重要的特征权重调整为0。
- 训练时,给模型只提供原始的特征,和最终顾客是否满意的 label。虽然整个系统由多个逻辑回归构成,但 训练时当做一个完整的模型。

经过上边的改进,就构造出了一个 神经网络,它可以看做是由 多个逻辑回归模型 经过 组合 构成的。
像上图中,只是设计了模型的架构,让模型在学习过程中,抽象出 3 个高级特征,具体这 3 个高级特征是什么?根据什么原始特征抽象?都是 让模型自己去学习。
然后根据抽象出的 3 个高级特征最后预测出顾客是否满意。提供的只有原始特征和最终顾客是否满意的 label 值,中间模型如何抽取高级特征对我们来说是黑盒。
神经网络在层层转换过程中,究竟在试图实现什么?
A Unique Perspective on What Hidden Layers and Activation Functions Do

在神经网络中,数据在每个隐藏层都会经历一系列转换。更具体地说,这涉及到每一层的以下操作:
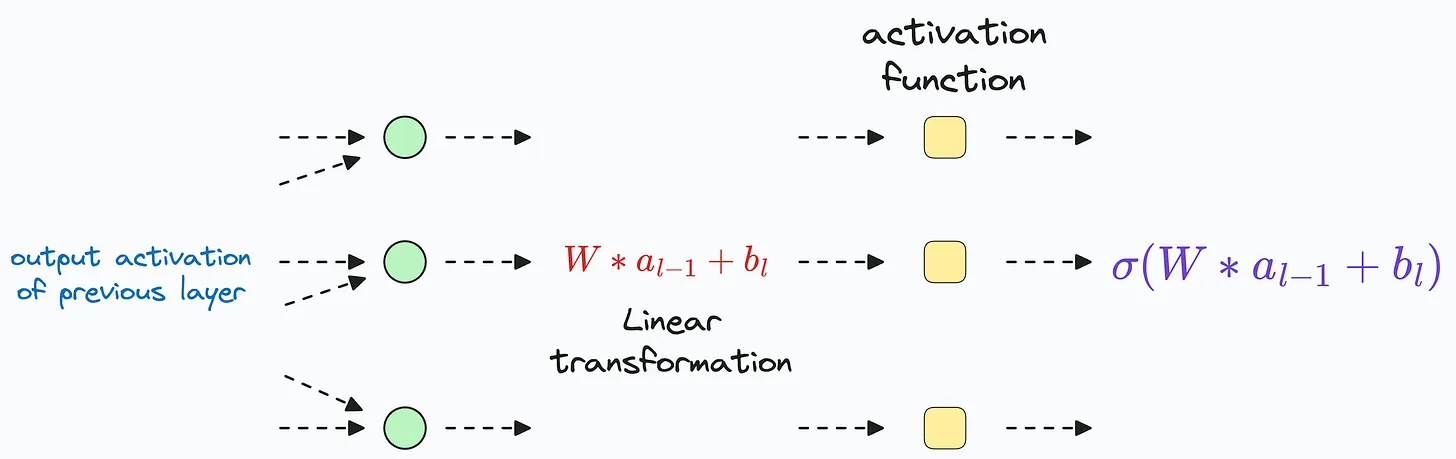
- 对来自前一层的数据进行 线性变换
- 随后使用 激活函数(如 ReLU、Sigmoid、Tanh 等)引入非线性
上述变换在神经网络的每个隐藏层中都会执行。
假设刚刚在神经网络的 最末隐藏层 上应用了上述数据变换,那么激活值会向网络的输出层推进,进行 最后一次变换,而这完全是线性的。

上述变换完全是线性的,因为所有非线性来源(激活函数)都存在于最末隐藏层及其之前。
而在前向传播过程中,一旦数据离开最末隐藏层,就不再有进一步的非线性空间。

因此,为了做出准确的预测,输出层从最后一个隐藏层接收到的数据必须是线性可分的。
总结一下,在将数据通过所有隐藏层进行转换,并且在即将到达输出层之前,神经网络不断努力将数据投影到一个使其某种程度上线性可分的空间。
如果实现了这一点,输出层就相当于一个逻辑回归模型,能够 轻松处理这些线性可分的数据。
事实上,也可以通过实验验证这一点。
为了可视化输入的变换,可以在输出层之前添加一个仅有两个神经元的虚拟隐藏层,然后再次训练神经网络。

这样,可以轻松地可视化变换。
我们预期,如果绘制这个二维虚拟隐藏层的激活,它们必须是线性可分的。下图准确地描绘了这一点。

正如上面注意到的,虽然 输入数据是线性不可分的,但 输出层接收到的输入确实是线性可分的。这些转换后的数据可以被输出分类层轻松处理。
这表明 神经网络所要做的全部就是 在到达输出层之前,将数据转换为线性可分的形式。
