数据结构——十七、线索二叉树找前驱与后继

前言

摘要：本文详细介绍了中序和先序线索二叉树中查找指定节点的前驱和后继的方法。对于中序线索二叉树，当rtag=1时后继为右孩子，rtag=0时需找到右子树最左下节点；前驱同理通过ltag判断。先序线索二叉树中，后继根据左右孩子存在情况决定，前驱则需通过三叉链表或逆向遍历实现。文章提供了各场景下的算法思路和完整代码实现，包括非递归的中序/先序遍历方法。

代码在文章开头,有需要自取🧐

一.中序线索二叉树找前驱/后继

1.在中序线索二叉树中找到指定结点*p的中序后继

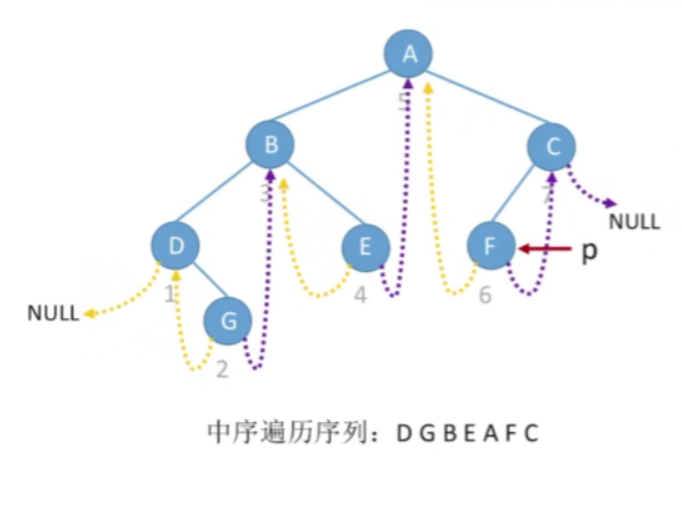
1.思路

1.若p->rtag == 1

• 则next=p->rchild

2.若p->rtag == 0

1.思路

1. 由于它的rtag等于0,就意味着这个指定节点它肯定是有右孩子的,既然找的是中序后继,也就是说我们要找的是按照中序遍历来看一个节点它后面一个被访问的节点
2. 而中序遍历的访问顺序应该是左根右,现在我们已经知道指定的节点p它肯定有右孩子,所以按照中序遍历的规则,访问p节点之后,需要在中序遍历右子树
3. 按照中序遍历的规则,它的右子树当中第一个被中序遍历的节点就应该是p的后继

   1. 访问p节点之后,假设p的右孩子已经是一个叶子结点,那么p的中序后继就是p的右孩子
      

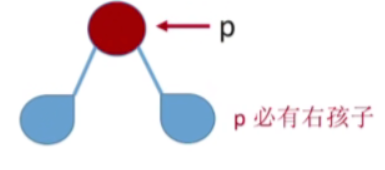
   2. 但是如果p的右孩子是一个分支节点,那么就要根据中序遍历的规则左根右,找到p的右孩子的左孩子,假设这个左孩子是一个叶子结点,那么p的中序后继就是这个左孩子
      

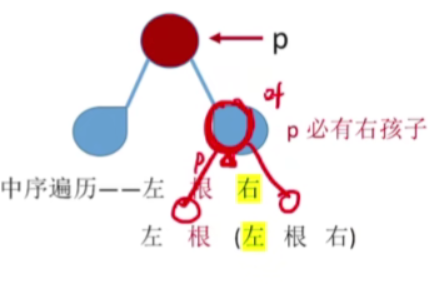
   3. 以此类推,总之p结点的后继是它的右子树中第一个被访问的元素

4. 总之:next=p的右子树中最左下结点就是p的后继节点,如果p的右孩子是叶子结点,那么p的后继就是它的右孩子

2.代码

//找到以P为根的子树中，第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p){p=p->rchild;//循环找到最左下结点(不一定是叶结点)while(p->ltag==0) p=p->lchild;return p;
}

2.代码

1.在中序线索二叉树中找到结点p的后继结点

//找到以P为根的子树中，第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p){//循环找到最左下结点(不一定是叶结点)while(p->ltag==0) p=p->lchild;return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p){//右子树中最左下结点if(p->rtag==0) return Firstnode(p->rchild);else return p->rchild; //rtag==1直接返回后继线索
}

2.对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)

//对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)
void Inorder(ThreadNode *T){for(ThreadNode *p=Firstnode(T); p!=NULL; p=Nextnode(p));visit(p);
}

2.在中序线索二叉树中找到指定结点*p的中序前驱pre

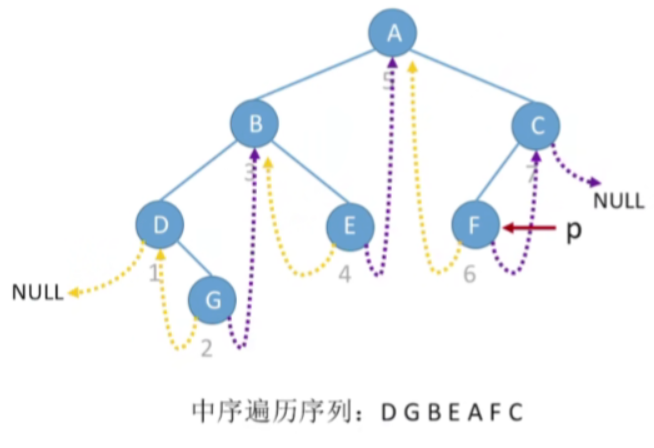
1.思路

1.若p->ltag == 1

• 则pre=p->lchild

2.若p->ltag == 0

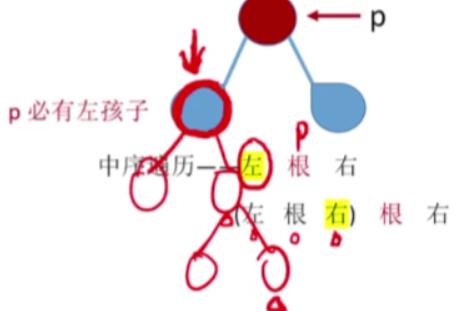
1.思路

1. 若p->ltag == 0,说明他肯定是有左孩子,那按照中序遍历的规则,我们的这个节点p它的前驱肯定是左子树当中按照中序遍历最后一个被访问的节点,思路与前面的找中序后继类似,不再展开
   

2. 总之,pre=p的左子树中最右下结点

2.代码

//找到以P为根的子树中，最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p){//循环找到最右下结点(不一定是叶结点)while(p->rtag==0) p=p->rchild;return p;
}

2.代码

1.在中序线索二叉树中找到结点p的前驱结点

//找到以P为根的子树中，最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p){//循环找到最右下结点(不一定是叶结点)while(p->rtag==0) p=p->rchild;return p;
}
//在中序线索二叉树中找到结点p的前驱结点
ThreadNode *Prenode(ThreadNode *p){//左子树中最右下结点if(p->ltag==0) return Ltenode(p->lchild);else return p->lchild;//ltag==1直接返回前驱线索
}

2.对中序线索二叉树进行逆向中序遍历

//对中序线索二叉树进行逆向中序遍历
void RevInorder(ThreadNode *T){
for(ThreadNode *p=Lastnode(T);p!=NULL;p=Prenode(p))visit(p);
}

从这里开始后面的代码风格不一致了,这个是因为后面王道没有放出代码,都是我自己写的,如果想查看完整代码,请下载本文开头的附件文件

二.先序线索二叉树找前驱/后继

1.在先序线索二叉树中找到指定结点*p的先序后继next

1.思路

1.若p-> rtag == 1

• 则next=p-> rchild

2.若 p->rtag == 0

1.思路

1. 若 p->rtag == 0,则p结点肯定有右孩子,但是他有没有左孩子,这个我们还不确定

2. 我们先假设这个节点它既有左孩子,又有右孩子
   

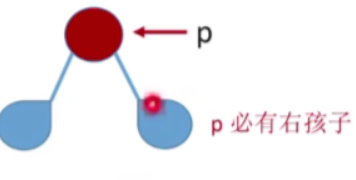
   1. 那么按照先序遍历根左右这样的规则来看,p节点的后继节点肯定是它左子树当中第一个被访问的节点
   2. 结论:若p有左孩子，则先序后继为左孩子

3. 再假设这个节点没有左孩子,只有右孩子
   

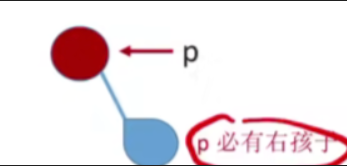
   1. 那按照先序遍历的规则,左根右,左子树为空,所以遍历的顺序就应该是根右,因此这种情况下,p声点它的后继肯定就是柚子树当中第一个被先序遍历的节点,在这里就是p的右孩子
   2. 结论:若p没有左孩子，则先序后继为右孩子

2.代码

if (treeNode->rtag == 0) {if (treeNode->lchild != NULL) {//左右孩子都不为空的时候,其左孩子就是其后继return treeNode->lchild;}else {return treeNode->rchild;//如果只有右孩子,则其后继为其右孩子}
}

2.代码

1.在先序线索二叉树中找到结点p的后继结点

//先序线索二叉树中寻找指定节点treeNode的先序后继
ThreadedBinaryTreeNode* PreThreadFindNextNode(ThreadedBinaryTreeNode* treeNode) {if (treeNode == NULL) return NULL;if (treeNode->rtag == 1) return treeNode->rchild;//右孩子就是后继线索时,直接返回右孩子if (treeNode->rtag == 0) {if (treeNode->ltag == 0) {//左右孩子都不为空的时候,其左孩子就是其后继return treeNode->lchild;}else {return treeNode->rchild;//如果只有右孩子,则其后继为其右孩子}}return NULL;
}

2.对先序线索二叉树进行先序遍历(利用线索实现的非递归算法)

//对先序线索二叉树进行先序遍历(利用线索实现的非递归算法)
bool ThreadBinaryTreePreOrder(ThreadedBinaryTree preOrderTree) {if (preOrderTree == NULL)return false;//先序遍历中第一个被访问的结点就是根节点printf("\n先序遍历序列的顺序序列为:");while (preOrderTree != NULL) {printf("%d ", preOrderTree->value);preOrderTree = PreThreadFindNextNode(preOrderTree);//找到其先序后继}return true;
}

2.在先序线索二叉树中找到指定结点*p的先序前驱pre

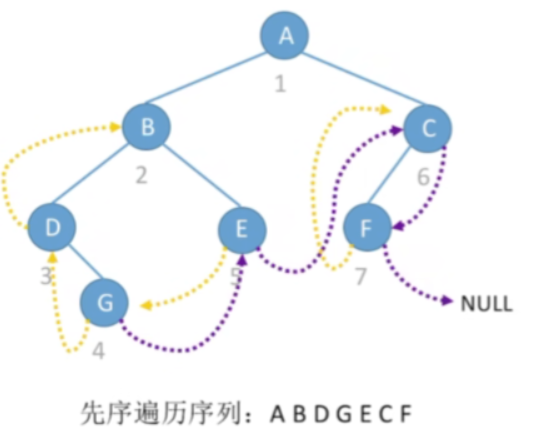
1.思路

1.若p->ltag == 1

• 则next=p->lchild

2.若p->ltag == 0

1.思路

1.常规思路行不通

1. 若p->ltag == 0,p它肯定有左孩子
   

2. 按照先序遍历的规则,p的左子树和右子树当中的所有的节点肯定都只可能是p的后继而不可能是p的前驱

3. 因此我们不可能在它的左右子树当中找到它的前驱

4. 而我们的线索二叉树它只有指向孩子节点的指针,不可能往回转,所以在这种情况下,我们是找不到p的先序前驱的

5. 除非用我们之前介绍从头开始便利的土办法,或者把二叉链表改成三叉链表

2.三叉链表

1. 如果能找到p的父节点，且p是左孩子
   

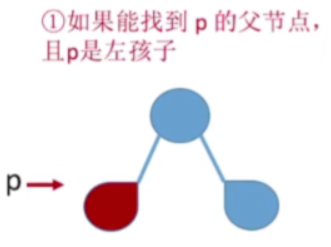
   • 按照先序遍历根左右,p节点肯定是在根节点也就是它父节点之后就被访问的一个节点,因此它的这个父节点一定就是它的前驱

2. 如果能找到p的父节点，且p是右孩子
   

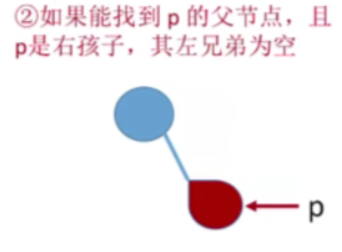
   • 那么按先序遍历根左右的这样的顺序,左子树为空,因此遍历的顺序就应该是根右,同样的p的这个父节点一定就是它的先序前驱

3. 如果能找到p的父节点，且p是右孩子，其左兄弟非空
   

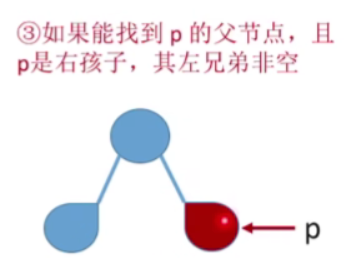
   • p这个节点的先序前驱一定是它的左兄弟子树当中最后一个被访问到的节点
     • 一棵树里边按照先序遍历的顺序,最后一个被访问的节点,我们应该从这个根节点出发,优先的往右边的路走,如果右边的路没有了,那我们应该往左边的路走,然后用这样的方式找到最下面一层的这个节点,这个节点就是先序遍历当中最后一个被访问的节点

4. 如果p是根节点(没有父节点)，则p没有先序前驱

2.代码(三叉链表实现)

if (treeNode->ltag == 0) {ThreadedBinaryTreeNode* parentTreeNode = treeNode->parent;//找到其父结点if (parentTreeNode == NULL) return NULL;//根节点无前驱if (parentTreeNode->lchild == treeNode || (parentTreeNode->ltag == 1 && parentTreeNode->rchild == treeNode)) {//左孩子为指定节点或者右孩子为指定节点且左孩子为空则前驱是其父结点return parentTreeNode;}//如果左右子树都不为空且右孩子就是这个节点,那么其先序前驱一定是它的左兄弟子树当中最后一个被访问到的节点if (parentTreeNode->ltag == 0 && parentTreeNode->rchild == treeNode) {parentTreeNode = parentTreeNode->lchild;while (1) {if (parentTreeNode->rtag == 0) {parentTreeNode = parentTreeNode->lchild;}else if (parentTreeNode->ltag == 0) {parentTreeNode = parentTreeNode->rchild;}//对于指定节点treeNode的右兄弟结点不为空的情况下,其父结点的左子树中不可能存在左右线索为空的结点//因此只需判断其左右孩子是否全部为线索即可找到该子树的最后一个结点if (parentTreeNode->rtag == 1 && parentTreeNode->ltag == 1) {break;}}return parentTreeNode;}

2.代码

1.在先序线索二叉树中找到结点p的前驱结点

//这里为了方便找到父结点,使用三叉链表
typedef struct ThreadedBinaryTree {//线索二叉树结点结构int value;//存储结点数据struct ThreadedBinaryTree* lchild;//指向左孩子struct ThreadedBinaryTree* rchild;//指向右孩子struct ThreadedBinaryTree* parent;//指向父结点int ltag, rtag;// 左/右线索标志,为0时说明结点左/右为孩子,为1时说明结点左/右为中序前驱/后继
}ThreadedBinaryTreeNode, * ThreadedBinaryTree;//先序线索二叉树中寻找指定节点treeNode的先序前驱
ThreadedBinaryTreeNode* PreThreadFindPreNode(ThreadedBinaryTreeNode* treeNode) {if (treeNode == NULL) return NULL;if (treeNode->ltag == 1) return treeNode->lchild;//右孩子就是前驱线索时,直接返回右孩子if (treeNode->ltag == 0) {ThreadedBinaryTreeNode* parentTreeNode = treeNode->parent;//找到其父结点if (parentTreeNode == NULL) return NULL;//根节点无前驱if (parentTreeNode->lchild == treeNode || (parentTreeNode->ltag == 1 && parentTreeNode->rchild == treeNode)) {//左孩子为指定节点或者右孩子为指定节点且左孩子为空则前驱是其父结点return parentTreeNode;}//如果左右子树都不为空且右孩子就是这个节点,那么其先序前驱一定是它的左兄弟子树当中最后一个被访问到的节点if (parentTreeNode->ltag == 0 && parentTreeNode->rchild == treeNode) {parentTreeNode = parentTreeNode->lchild;while (1) {if (parentTreeNode->rtag == 0) {parentTreeNode = parentTreeNode->lchild;}else if (parentTreeNode->ltag == 0) {parentTreeNode = parentTreeNode->rchild;}//对于指定节点treeNode的右兄弟结点不为空的情况下,其父结点的左子树中不可能存在左右线索为空的结点//因此只需判断其左右孩子是否全部为线索即可找到该子树的最后一个结点if (parentTreeNode->rtag == 1 && parentTreeNode->ltag == 1) {break;}}return parentTreeNode;}}return NULL;
}

2.对先序线索二叉树进行逆向先序遍历(利用线索实现的非递归算法)

//对前序线索二叉树进行逆向前序遍历(利用线索实现的非递归算法)
bool ThreadBinaryTreeRevPreOrder(ThreadedBinaryTree revPreOrderTree) {if (revPreOrderTree == NULL)return false;//找到最后一个结点//右边有路优先右边,没路则往左边,直至找到叶子结点while (1) {if (revPreOrderTree->rtag == 0) {revPreOrderTree = revPreOrderTree->rchild;}else if(revPreOrderTree->ltag != 0){revPreOrderTree = revPreOrderTree->lchild;}//当左孩子连接前驱结点,右孩子为NULL时,为最后一个结点if(revPreOrderTree->ltag == 1 && revPreOrderTree->rchild == NULL){break;}}printf("\n先序遍历序列的逆序序列为:");while (revPreOrderTree != NULL) {printf("%d ", revPreOrderTree->value);revPreOrderTree = PreThreadFindPreNode(revPreOrderTree);//找到其先序前驱}return true;
}

三.后序线索二叉树找后序前驱/后继

1.在后序线索二叉树中找到指定结点*p的后序前驱pre

1.思路

1.若p->ltag == 1

• 则 pre = p-> lchild

2.若p->ltag == 0

1.思路

1. 若p->ltag == 0,p结点一定有左孩子,但是他有没有右孩子我们不知道

2. 假设p结点既有左孩子,又有右孩子
   

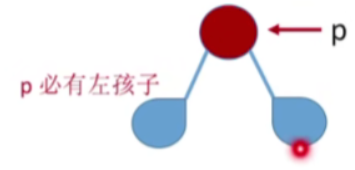
   1. 按照后续遍历左右根的便利顺序可以看到p这个节点,它的后续前驱一定是它的右子树当中按照后续遍历最后一个被访问到的节点,那显然p的右孩子一定是最后一个被访问到的
   2. 结论:若p有右孩子，则后序驱为右孩子

3. 假设p结点只有左孩子,没有右孩子
   

   1. 按照左右根的遍历顺序,右子树为空,那就是左根,p这个节点的前驱应该就是左子树当中按照后续遍历最后一个被访问的节点,那显然就应该是它的左孩子
   2. 结论:若p没有右孩子，则后序前驱为左孩子

if (treeNode->ltag == 0) {if (treeNode->rchild != NULL) {//左右孩子都不为空的时候,其右孩子就是其前驱return treeNode->rchild;}else {return treeNode->lchild;//如果只有左孩子,则其前驱为其左孩子}
}

2.代码

//后序线索二叉树中寻找指定节点treeNode的后序前驱
ThreadedBinaryTreeNode* PostThreadFindPreNode(ThreadedBinaryTreeNode* treeNode) {if (treeNode == NULL) return NULL;if (treeNode->ltag == 1) return treeNode->lchild;//右孩子就是前驱线索时,直接返回右孩子if (treeNode->ltag == 0) {if (treeNode->rchild == 0) {//左右孩子都不为空的时候,其右孩子就是其前驱return treeNode->rchild;}else {return treeNode->lchild;//如果只有左孩子,则其前驱为其左孩子}}return NULL;
}

2.在后序线索二叉树中找到指定结点*p的后序后继pre

1.思路

1.若p->rtag == 1

• 则next=p->rchild

2.若p->rtag == 0

1.思路

1.常规思路行不通

• p结点的左右子树中的所有节点一定只有可能是它的前驱,找不到后继
• 解决方法:重新进行后驱遍历或者三叉链表

2.三叉链表

1. 如果能找到p的父节点，且p是右孩子
   

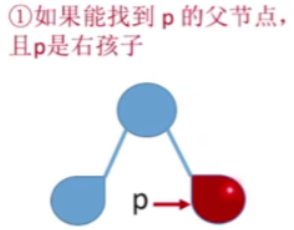
   • p的父节点即为其后继

2. 如果能找到p的父节点，且p是左孩子，其右兄弟为空
   

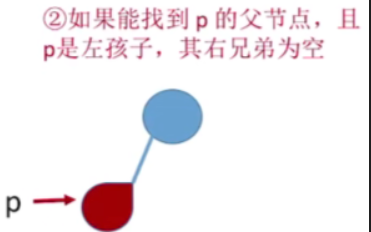
   • p的父节点即为其后继

3. 如果能找到p的父节点，且p是左孩子，其右兄弟非空
   

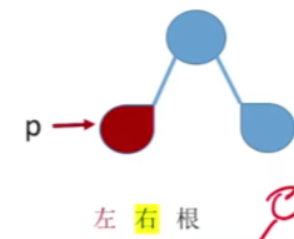
   • p的后继为右兄弟子树中第一个被后序遍历的结点
   • 第一个被访问的节点应该是我们可以从根节点出发,然后尽可能的往左走,如果往左的路没了但是还有往右的路的话,那我们还要继续往右走,用这种方式找到最下面的一个叶子节点,它就是第一个被后续遍历的节点

4. 如果p是根节点(无父节点)，则p没有后序后继

2.代码

if (treeNode->rtag == 0) {ThreadedBinaryTreeNode* parentTreeNode = treeNode->parent;//找到其父结点if (parentTreeNode == NULL) return NULL;//根节点无后继if (parentTreeNode->rchild == treeNode || (parentTreeNode->rtag == 1 && parentTreeNode->lchild == treeNode)) {//右孩子为指定节点或者左孩子为指定节点且右孩子为空则前驱是其父结点return parentTreeNode;}//如果左右子树都不为空且左孩子就是这个节点,那么其后序后继一定是它的右兄弟子树当中第一个被访问到的节点if (parentTreeNode->rtag == 0 && parentTreeNode->lchild == treeNode) {parentTreeNode = parentTreeNode->rchild;while (1) {if (parentTreeNode->ltag == 0) {parentTreeNode = parentTreeNode->lchild;}else if (parentTreeNode->rtag == 0) {parentTreeNode = parentTreeNode->rchild;}//右兄弟子树中一定不可能出现第一个被访问的结点//因此该只需判断是否全为线索即可if (parentTreeNode->ltag == 1 && parentTreeNode->rtag == 1){break;}}return parentTreeNode;}
}

2.代码

//这里为了方便找到父结点,使用三叉链表
typedef struct ThreadedBinaryTree {//线索二叉树结点结构int value;//存储结点数据struct ThreadedBinaryTree* lchild;//指向左孩子struct ThreadedBinaryTree* rchild;//指向右孩子struct ThreadedBinaryTree* parent;//指向父结点int ltag, rtag;// 左/右线索标志,为0时说明结点左/右为孩子,为1时说明结点左/右为中序前驱/后继
}ThreadedBinaryTreeNode, * ThreadedBinaryTree;//后序线索二叉树中寻找指定节点treeNode的后序后继
ThreadedBinaryTreeNode* PostThreadFindNextNode(ThreadedBinaryTreeNode* treeNode) {if (treeNode == NULL) return NULL;if (treeNode->rtag == 1) return treeNode->rchild;//右孩子就是后继线索时,直接返回右孩子if (treeNode->rtag == 0) {ThreadedBinaryTreeNode* parentTreeNode = treeNode->parent;//找到其父结点if (parentTreeNode == NULL) return NULL;//根节点无后继if (parentTreeNode->rchild == treeNode || (parentTreeNode->rtag == 1 && parentTreeNode->lchild == treeNode)) {//右孩子为指定节点或者左孩子为指定节点且右孩子为空则前驱是其父结点return parentTreeNode;}//如果左右子树都不为空且左孩子就是这个节点,那么其后序后继一定是它的右兄弟子树当中第一个被访问到的节点if (parentTreeNode->rtag == 0 && parentTreeNode->lchild == treeNode) {parentTreeNode = parentTreeNode->rchild;while (1) {if (parentTreeNode->ltag == 0) {parentTreeNode = parentTreeNode->lchild;}else if (parentTreeNode->rtag == 0) {parentTreeNode = parentTreeNode->rchild;}//右兄弟子树中一定不可能出现第一个被访问的结点//因此该只需判断是否全为线索即可if (parentTreeNode->ltag == 1 && parentTreeNode->rtag == 1){break;}}return parentTreeNode;}}return NULL;
}

四.知识回顾与重要考点

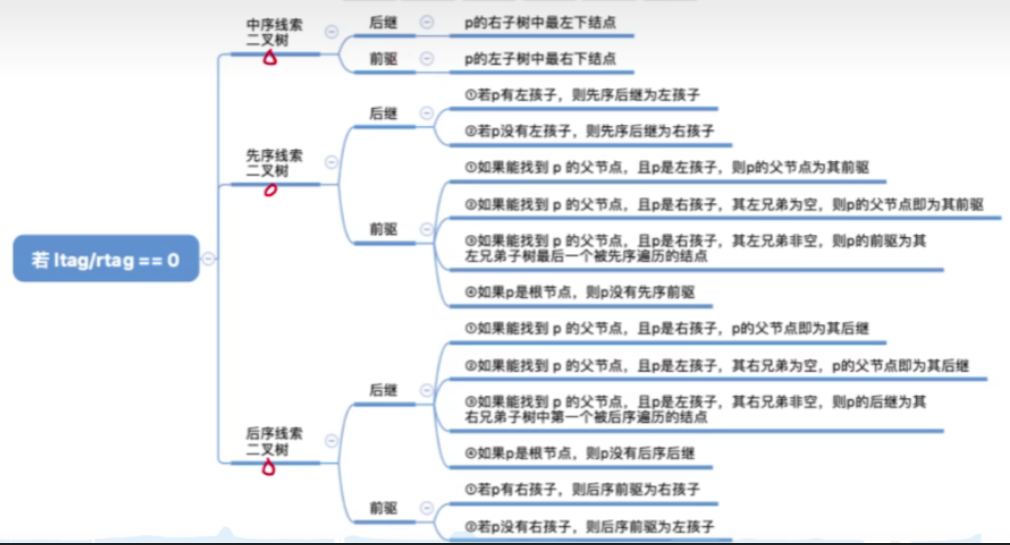
	中序线索二叉树	先序线索二叉树	后序线索二叉树
找前驱	✔	✗	✔
找后继	✔	✔	✗

• 除非用三叉链表，或者用土办法从根开始遍历寻找
  

结语

第二更😉

如果想要看更多章节,请点击一、数据结构专栏导航页（王道408）