当前位置：首页 > news >正文

C++递归函数

news 2025/10/8 15:15:08

C++递归函数

一、递归基础概念

1. 什么是递归？

递归就是函数自己调用自己。就像俄罗斯套娃，大娃娃里面装着一个小娃娃，小娃娃里面又装着更小的娃娃。

2. 递归的两个必要条件

基准条件：什么时候停止递归（必须有）
递归条件：如何把大问题变成小问题（必须有）

二、递归入门示例

示例1：倒计时函数

void countDown(int n) {
// 基准条件if (n == 0) {cout << "发射！" << endl;return;}// 递归条件cout << n << "..." << endl;countDown(n - 1);// 调用自己
}// 调用
countDown(5);// 输出5...4...3...2...1...发射！

示例2：求1+2+...+n的和

int sum(int n) {
// 基准条件if (n == 1) return 1;// 递归条件return n + sum(n - 1);
}// 调用
cout << sum(100);// 输出5050

三、递归执行过程详解

以sum(3)为例分析调用栈

sum(3) → 需要计算 3 + sum(2)↓sum(2) → 需要计算 2 + sum(1)↓sum(1) → 基准条件返回1↑sum(2) ← 2 + 1 = 3↑
sum(3) ← 3 + 3 = 6

四、经典递归问题

1. 阶乘计算

int fac(int n) {
// 基准条件if (n == 0 || n == 1) return 1;// 递归条件return n * fac(n - 1);
}// 调用
cout << fac(5);// 输出120 (5! = 120)

2. 斐波那契数列

int fib(int n) {
// 基准条件if (n == 0) return 0;if (n == 1) return 1;// 递归条件return fib(n - 1) + fib(n - 2);
}// 调用
cout << fib(6);// 输出8 (0,1,1,2,3,5,8)

3. 数字各位相加

int digitSum(int n) {
// 基准条件if (n < 10) return n;// 递归条件return n % 10 + digitSum(n / 10);
}// 调用
cout << digitSum(123);// 输出6 (1+2+3)

五、递归常见错误

错误1：缺少基准条件

// 错误示例：无限递归！
void forever(int n) {cout << n << endl;forever(n + 1);// 没有停止条件！
}

错误2：递归条件不收敛

// 错误示例：永远不会到达基准条件
int wrongFac(int n) {if (n == 1) return 1;return n * wrongFac(n);// 没有减小n的值！
}

六、递归练习题目

编写递归函数计算x的n次方

double pow(double x, int n);
/*
double pow(double x, int n) {if (n == 0) return 1;return x * pow(x, n - 1);
}
*/

递归判断一个数是否是偶数（不使用%运算符）

bool isEven(int n);
/*
bool isEven(int n) {if (n == 0) return true;if (n == 1) return false;return isEven(n - 2);
}
*/

递归输出数字的二进制形式

void CT(int n);
/*
void CT(int n) {if (n == 0) return;CT(n / 2);cout << n % 2;
}
*/

七、递归与循环对比

特性	递归	循环
代码量	少	多
内存使用	多（调用栈）	少
适用问题	分治问题	简单重复问题
可读性	高（数学思维）	低

八、总结要点

所有递归必须有两个部分：

基准条件（什么时候停止）
递归条件（如何缩小问题规模）

递归调用会使用调用栈，深度过大会导致栈溢出
递归代码通常比循环更简洁，但效率可能更低
练习时建议画调用栈图帮助理解执行过程

九、课堂训练

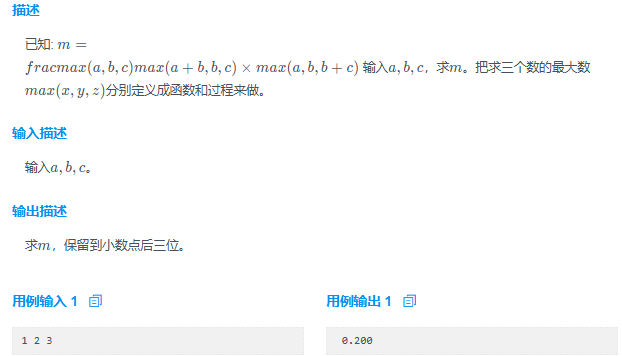
最大数max(x,y,z)

#include <bits/stdc++.h>
using namespace std;
double max(double x,double y,double z){double maxn=x;if(y>maxn) maxn=y;if(z>maxn) maxn=z;return maxn;
}
int main(){double a,b,c;cin>>a>>b>>c;double m=max(a,b,c) / (max(a+b,b,c)*max(a,b,b+c));printf("%.3lf",m);return 0;
}

编程求解1+2+3+...+n

描述

编程求解下列式子的值：S=1+2+3+…+n

输入描述

输入一行，只有一个整数n(1<=n<=1000)

输出描述

输出只有一行（这意味着末尾有一个回车符号），包括1个整数。

用例输入 1

100

用例输出 1

5050

#include <bits/stdc++.h>
using namespace std;
int n,sum=0;
void f(int i){sum=sum+i;if(i==n) return;f(i+1);
}
int main() {cin>>n;f(1);cout<<sum;return 0;
}

请输出n~1之间所有的整数

描述

从键盘读入一个整数n，请输出n~1之间所有的整数，每行输出1个。
比如，假设读入n=5，输出结果如下：
5
4
3
2
1

输入描述

一个整数n。

输出描述

输出n~1之间所有的数，每行1个。

用例输入 1

用例输出 1

#include <bits/stdc++.h>
using namespace std;
int n;
void f(int i){cout<<i<<endl;if(i==1) return;f(i-1);
}
int main() {cin>>n;f(n);return 0;
}

请输出1~n之间所有的整数

描述

从键盘读入一个整数n，请循环输出1~n之间所有的整数，每行输出1个。
比如，假设n=5，那么输出结果如下：
1
2
3
4
5

输入描述

一个整数n。

输出描述

输出1~n之间所有的整数。

用例输入 1

用例输出 1

#include <bits/stdc++.h>
using namespace std;
int n;
void f(int i) {cin>>n;cout<<i<<endl;if(i==n) {return;}f(i+1);
}
int main() {f(1);return 0;
}

数列求和

描述

有一数列如下： 1 2 4 7 11 16 22…… 试求该数列前N项之和。

输入描述

一个整数N（ 0 < N < 1000 ）。

输出描述

一个整数。

用例输入 1

用例输出 1

#include <bits/stdc++.h>
using namespace std;
int s=0; //累加和 
int t=1; //第一项
int n; 
void f(int i){t=t+i;//下一项的值 s=s+t;if(i==n-1) return;f(i+1); 
}int main(){cin>>n;f(0);cout<<s;return 0;
}
/*
1+0
1+1
2+2
4+3
7+4
11+5
16+6
*/

数数小木块

描述

在墙角堆放着一堆完全相同的正方体小木块，如下图所示：

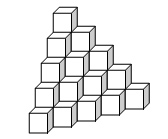
因为木块堆得实在是太有规律了，你只要知道它的层数就可以计算所有木块的数量了。

输入描述

只有一个整数 n ，表示这堆小木块的层数，已知1 <= n <= 100 。

输出描述

只有一个整数，表示这堆小木块的总数量。

用例输入 1

用例输出 1

#include <iostream>
using namespace std;
int ans(int n) {if (n == 1) { // 基准情况：1层只有1个木块return 1;} else {// 递归关系：n层总数 = (n-1)层总数 + 第n层的木块数（三角形数T_n）return ans(n - 1) + n * (n + 1) / 2;}
}
int main() {int n;cin >> n; // 输入层数cout << ans(n) << endl; // 输出结果return 0;
}

尾递归优化

#include <iostream>
using namespace std;// 尾递归辅助函数：n=总层数，c=当前层，a=累加器
int trc(int n, int c, int a) {if (c > n) return a; // 当前层超总数，返回累加结果int l = c * (c + 1) / 2; // 当前层木块数（l=layer）return trc(n, c + 1, a + l); // 递归累加下一层
}// 计算n层木块总数（对外接口）
int cnt(int n) {return trc(n, 1, 0); // 从第1层开始，初始累加0
}int main() {int n;cin >> n;cout << cnt(n) << endl;return 0;
}

汉诺塔的移动次数

描述

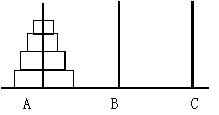
汉诺塔的问题大家都已经很熟悉了，有三个柱子，每个柱子上有一些大小不一的金片，要把金片从A柱移动到C柱，可以借助B柱，请问n个金片的情况下，需要最少移动多少次？

输入描述

输入一个整数n代表金片的数量（n<=20）

输出描述

一个整数，代表n个金片的移动次数

用例输入 1

用例输出 1

#include <iostream>
using namespace std;
// 递归函数：计算n个盘子的移动次数（h=hanoi）
int h(int n) {if (n == 1) {    // 基准情况：1个盘子需1次return 1;} else {         // 递归情况：n个盘子 = 2*h(n-1) + 1return 2 * h(n - 1) + 1;}
}
int main() {int n;cin >> n;       // 输入盘子数ncout << h(n);   // 输出移动次数return 0;
}

求1/1+1/2+2/3+3/5+5/8+8/13+13/21……的前n项的和

描述

求1/1+1/2+2/3+3/5+5/8+8/13+13/21+21/34……的前n项的和。

输入描述

第1行：一个整数n（1 <= n <= 30 ）。

输出描述

一行：一个小数，即前n项之和（保留3位小数）。

用例输入 1

用例输出 1

12.660

#include <bits/stdc++.h>
using namespace std;
double sum=0; //累加和 
int n;
void f(double a,double b,int i){sum=sum+a/b; //把当前项加到sum中if(i==n) return; //递归走下一项 f(b,a+b,i+1); 
} 
int main(){cin>>n;f(1,1,1);// f(分子,分母,第几项)	printf("%.3lf",sum); return 0;
}
/*
当前项：分母 = 上一项的分子+分母分子 = 上一项的分母
1/11/22/3	3/55/8..... */

求S的值

描述

求S=1+2+4+7+11+16……的值刚好大于等于5000时S的值。

输入描述

无

输出描述

一行，一个整数。

#include <bits/stdc++.h>
using namespace std;
int s=1; //累加和 
int t=1; 
void f(int i){t=t+i;s=s+t;if(s>=5000) return;f(i+1); 
}
int main(){f(1);cout<<s;return 0;
}
/*
1+1
2+2
4+3
7+4
11+5
16+6
*/

查看全文

http://www.dtcms.com/a/454956.html