扩散模型DDPM数学推导过程完整版(上)
文章目录
- DDPM模型
- 加噪阶段(noising)
- 去噪阶段(denoising)
- 参考文献
DDPM模型
扩散模型的工作原理可以类比于建筑拆除与重建的过程。
加噪阶段:原始图像像一栋完整的大楼,通过逐步添加噪声,相当于将大楼拆解成零散的建筑材料,最终得到完全无序的噪声状态。
去噪学习阶段:模型通过学习如何从噪声分布中逐步重建图像,类似于利用拆解后的建筑材料重新搭建一栋与原建筑相似的大楼。
整个过程体现了从有序到无序,再从无序恢复有序的逆向学习机制。

加噪阶段(noising)
给定真实数据分布q(x0)q(x_0)q(x0),定义一个长度为TTT的马尔可夫加噪过程:
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI),t=1,…,Tq(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}\left.x_{t-1},\beta_t\mathbf{I}\right),\quad t=1,\ldots,Tq(xt∣xt−1)=N(xt;1−βtxt−1,βtI),t=1,…,T
其中{βt}∈(0,1)\{\beta_t\}\in(0,1){βt}∈(0,1)是固定噪声日程(DDPM原始论文使用的是线性递增的方式,T=1000,β1=10−4,βT=0.02T=1000,\beta_1=10^{-4},\beta_T=0.02T=1000,β1=10−4,βT=0.02)
符号解释
- q(xt∣xt−1)q(x_t\mid x_{t-1})q(xt∣xt−1):表示一个条件分布,意思是“给定上一步的随机变量xt−1x_{t-1}xt−1,这一步xtx_txt的分布“。
- N(μ,Σ)\mathcal{N}(\mu,\Sigma)N(μ,Σ):表示高斯分布(正态分布),μ\muμ是均值,Σ\SigmaΣ是协方差矩阵。
- 1−βtxt−1\sqrt{1-\beta_t}x_{t-1}1−βtxt−1:均值部分,说明xtx_txt大致围绕着缩小一点的xt−1x_{t-1}xt−1摆动。
- βtI\beta_t\mathbf{I}βtI:协方差(噪声强度)。I\mathbf{I}I是单位矩阵,表示各个维度独立同分布,方差为βt\beta_tβt。
将q(xt∣xt−1)q(x_t\mid x_{t-1})q(xt∣xt−1)写成重参数化形式即:
xt=1−βtxt−1+βtε,ε∼N(0,I)x_t=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}\varepsilon,\quad\varepsilon\sim\mathcal{N}(0,I)xt=1−βtxt−1+βtε,ε∼N(0,I)
如果一个随机变量
X∼N(μ,σ2I)X\sim\mathcal{N}(\mu,\sigma^2I)X∼N(μ,σ2I)
那么你总可以写成
X=μ+σε,ε∼N(0,I).X=\mu+\sigma\varepsilon,\quad\varepsilon\sim\mathcal{N}(0,I).X=μ+σε,ε∼N(0,I).
我们令αt=1−βt,αˉt=∏s=1tαs\alpha_t=1-\beta_t,\quad\bar{\alpha}_t=\prod_{s=1}^t\alpha_sαt=1−βt,αˉt=∏s=1tαs,有:
xt=αtxt−1+1−αtε1=αt(αt−1xt−2+1−αt−1ε2)+1−αtε1=αtαt−1xt−2+αt1−αt−1ε2+1−αtε1=αtαt−1xt−2+1−αtαt−1ε=......=αtαt−1⋅......⋅α1x0+1−αtαt−1⋅......⋅α1⋅ε=αˉtx0+1−αˉtε\begin{aligned} x_t&=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\varepsilon_1 \\&=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\varepsilon_2)+\sqrt{1-\alpha_t}\varepsilon_1 \\&=\sqrt{\alpha_t}\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\varepsilon_2+\sqrt{1-\alpha_t}\varepsilon_1 \\&=\sqrt{\alpha_t}\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}}\varepsilon \\&=...... \\&=\sqrt{\alpha_t}\sqrt{\alpha_{t-1}}\cdot......\cdot\sqrt{\alpha_1}x_0+\sqrt{1-\alpha_t \alpha_{t-1}\cdot......\cdot\alpha_1}\cdot\varepsilon \\&=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\varepsilon \end{aligned}xt=αtxt−1+1−αtε1=αt(αt−1xt−2+1−αt−1ε2)+1−αtε1=αtαt−1xt−2+αt1−αt−1ε2+1−αtε1=αtαt−1xt−2+1−αtαt−1ε=......=αtαt−1⋅......⋅α1x0+1−αtαt−1⋅......⋅α1⋅ε=αˉtx0+1−αˉtε
其中ε∼N(0,I)\varepsilon\sim\mathcal{N}(0,I)ε∼N(0,I)。
其中η=αt1−αt−1ε2+1−αtε1,ε1,ε2∼i.i.d.N(0,I).\eta=\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\varepsilon_2+\sqrt{1-\alpha_t}\varepsilon_1,\quad\varepsilon_1,\varepsilon_2\overset{\mathrm{i.i.d.}}{\operatorname*{\operatorname*{\sim}}}\mathcal{N}(0,I).η=αt1−αt−1ε2+1−αtε1,ε1,ε2∼i.i.d.N(0,I).
E(η)=0E(\eta)=0E(η)=0
Cov(η)=αt(1−αt−1)I+(1−αt)I=(1−αtαt−1)ICov(\eta)=\alpha_t(1-\alpha_{t-1})I+(1-\alpha_t)I=(1-\alpha_t\alpha_{t-1})ICov(η)=αt(1−αt−1)I+(1−αt)I=(1−αtαt−1)I
故η∼N(0,(1−αtαt−1)I)\eta\sim\mathcal{N}(0,(1-\alpha_t\alpha_{t-1})I)η∼N(0,(1−αtαt−1)I)
所以根据高斯分布的重参数化有:
η=1−αtαt−1ε,ε∼N(0,I)\eta=\sqrt{1-\alpha_t \alpha_{t-1}}\varepsilon,\quad\varepsilon\sim\mathcal{N}(0,I)η=1−αtαt−1ε,ε∼N(0,I)
现在我们跳过了逐步加噪的过程,只需一步加噪(xt=αˉtx0+1−αˉtεx_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\varepsilonxt=αˉtx0+1−αˉtε)就能显著提升算法的整体效率!
去噪阶段(denoising)
去噪阶段的目标是学习上一步加噪阶段的近似q(xt−1∣xt)q(x_{t-1}\mid x_t)q(xt−1∣xt)的后验分布:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
上一步加噪阶段的后验分布为:
q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(x_{t-1}\mid x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}(x_t,x_0),\tilde{\beta}_t\mathbf{I})q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)
利用贝叶斯理论的推广公式:
q(xt−1∣xt,x0)=q(xt∣xt−1)q(xt−1∣x0)q(xt∣x0)q(x_{t-1}\mid x_t,x_0)=\frac{q(x_t\mid x_{t-1})q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1)q(xt−1∣x0)
我们已知
{q(xt∣xt−1)=N(αtxt−1,(1−αt)I)q(xt−1∣x0)=N(αˉt−1x0,(1−αˉt−1)I)q(xt∣x0)=N(αˉtx0,(1−αˉt)I)\begin{cases} q(x_t\mid x_{t-1})=\mathcal{N}\left(\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I\right) \\q(x_{t-1}\mid x_0)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{t-1}}x_0,(1-\bar{\alpha}_{t-1})I\right) \\q(x_t\mid x_0)=\mathcal{N}\left(\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)I\right)& \end{cases}⎩⎨⎧q(xt∣xt−1)=N(αtxt−1,(1−αt)I)q(xt−1∣x0)=N(αˉt−1x0,(1−αˉt−1)I)q(xt∣x0)=N(αˉtx0,(1−αˉt)I)
我们可以写出它们的概率密度函数
{f(xt∣xt−1)=12πβtexp[−(xt−αtxt−1)22βt]f(xt−1∣x0)=12π(1−αˉt−1)exp[−(xt−1−αˉt−1x0)22(1−αˉt−1)]f(xt∣x0)=12π(1−αˉt)exp[−(xt−αˉtx0)22(1−αˉt)]\begin{cases} f(x_t\mid x_{t-1})=\frac{1}{\sqrt{2\pi\beta_t}}exp[-\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{2\beta_t}] \\f(x_{t-1}\mid x_0)=\frac{1}{\sqrt{2\pi(1-\bar{\alpha}_{t-1})}}exp[-\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{2(1-\bar{\alpha}_{t-1})}] \\f(x_t\mid x_0)=\frac{1}{\sqrt{2\pi(1-\bar{\alpha}_t)}}exp[-\frac{(x_t-\sqrt{\bar{\alpha}_t}x_0)^2}{2(1-\bar{\alpha}_t)}]& \end{cases}⎩⎨⎧f(xt∣xt−1)=2πβt1exp[−2βt(xt−αtxt−1)2]f(xt−1∣x0)=2π(1−αˉt−1)1exp[−2(1−αˉt−1)(xt−1−αˉt−1x0)2]f(xt∣x0)=2π(1−αˉt)1exp[−2(1−αˉt)(xt−αˉtx0)2]
最终q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0)的概率密度函数一定能写成f(xt−1∣xt,x0)=12πβ~texp[−(xt−1−μ~(xt,x0))22β~t]f(x_{t-1}\mid x_t,x_0)=\frac{1}{\sqrt{2\pi\tilde{\beta}_t}}exp[-\frac{(x_{t-1}-\tilde{\mu}(x_t,x_0))^2}{2\tilde{\beta}_t}]f(xt−1∣xt,x0)=2πβ~t1exp[−2β~t(xt−1−μ~(xt,x0))2]
故f(xt−1∣xt,x0)=f(xt∣xt−1)f(xt−1∣x0)f(xt∣x0)f(x_{t-1}\mid x_t,x_0)=\frac{f(x_t\mid x_{t-1})f(x_{t-1}\mid x_0)}{f(x_t\mid x_0)}f(xt−1∣xt,x0)=f(xt∣x0)f(xt∣xt−1)f(xt−1∣x0)
我们现在先算q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0)的方差β~t\tilde{\beta}_tβ~t,只算指数函数前面的系数即可:
12πβt⋅12π(1−αˉt−1)12π(1−αˉt)=12π⋅(1−αˉt−11−αˉt⋅βt)\frac{\frac{1}{\sqrt{2\pi\beta_t}}\cdot\frac{1}{\sqrt{2\pi(1-\bar{\alpha}_{t-1})}}}{\frac{1}{\sqrt{2\pi(1-\bar{\alpha}_t)}}}=\frac{1}{\sqrt{2\pi\cdot(\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}}\cdot\beta_t)}2π(1−αˉt)12πβt1⋅2π(1−αˉt−1)1=2π⋅(1−αˉt1−αˉt−1⋅βt)1
故可得出β~t=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_tβ~t=1−αˉt1−αˉt−1⋅βt。
然后我们再算q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0)的均值μ~(xt,x0)\tilde{\mu}(x_t,x_0)μ~(xt,x0),只计指数部分即可:
−12⋅((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1+(xt−αˉtx0)21−αˉt)-\frac{1}{2}\cdot(\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t}+\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{1-\bar{\alpha}_{t-1}}+\frac{(x_t-\sqrt{\bar{\alpha}_t}x_0)^2}{1-\bar{\alpha}_t})−21⋅(βt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2+1−αˉt(xt−αˉtx0)2)
我们可以发现这个式子中与xt−1x_{t-1}xt−1有关的项只有前两项,最后一项只影响其值域,不影响均值和方差,故式子可以化简为(只需要凑出(xt−1−μ~(xt,x0))2β~t\frac{(x_{t-1}-\tilde{\mu}(x_t,x_0))^2}{\tilde{\beta}_t}β~t(xt−1−μ~(xt,x0))2):
(xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1=(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βtβt(1−αˉt−1)=[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]/(1−αˉt)β~t\begin{aligned} &\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t}+\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{1-\bar{\alpha}_{t-1}} \\=&\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2(1-\bar{\alpha}_{t-1})+(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2\beta_t}{\beta_t(1-\bar{\alpha}_{t-1})} \\=&\frac{[(x_t-\sqrt{\alpha_t}x_{t-1})^2(1-\bar{\alpha}_{t-1})+(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2\beta_t]/(1-\bar{\alpha}_t)}{\tilde{\beta}_t} \end{aligned}==βt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2βt(1−αˉt−1)(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βtβ~t[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]/(1−αˉt)
故此我们就可以直接将E=[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]E=[(x_t-\sqrt{\alpha_t}x_{t-1})^2(1-\bar{\alpha}_{t-1})+(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2\beta_t]E=[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]凑成[xt−1−μ~(xt,x0)]2[x_{t-1}-\tilde{\mu}(x_t,x_0)]^2[xt−1−μ~(xt,x0)]2的形式。
为了方便书写和运算,我们将该表达式记作:
E=A(xt−axt−1)2+B(xt−1−bx0)2E=A(x_t-ax_{t-1})^2+B(x_{t-1}-bx_0)^2E=A(xt−axt−1)2+B(xt−1−bx0)2
其中A=1−αˉt−1A=1-\bar{\alpha}_{t-1}A=1−αˉt−1,B=βtB=\beta_tB=βt,a=αta=\sqrt{\alpha_t}a=αt,b=αˉt−1b=\sqrt{\bar{\alpha}_{t-1}}b=αˉt−1。
先展开两项的平方和即:
{(xt−axt−1)2=a2xt−12−2axtxt−1+xt2(xt−1−bx0)2=xt−12−2bx0xt−1+b2x02\begin{cases} (x_t-ax_{t-1})^2=a^2x_{t-1}^2-2ax_tx_{t-1}+x_t^2 \\(x_{t-1}-bx_0)^2=x_{t-1}^2-2bx_0x_{t-1}+b^2x_0^2 \end{cases}{(xt−axt−1)2=a2xt−12−2axtxt−1+xt2(xt−1−bx0)2=xt−12−2bx0xt−1+b2x02
接着按照xt−1x_{t-1}xt−1的幂次进行收集:
E=A(a2xt−12−2axtxt−1+xt2)+B(xt−12−2bx0xt−1+b2x02)=(Aa2+B)xt−12−2(Aaxt+Bbx0)xt−1+(Axt2+Bb2x02)\begin{aligned} E=&A\left(a^2x_{t-1}^2-2ax_tx_{t-1}+x_t^2\right)+B\left(x_{t-1}^2-2bx_0x_{t-1}+b^2x_0^2\right) \\=&\left(Aa^2+B\right)x_{t-1}^2-2(Aax_t+Bbx_0)x_{t-1}+(Ax_t^2+Bb^2x_0^2) \end{aligned}E==A(a2xt−12−2axtxt−1+xt2)+B(xt−12−2bx0xt−1+b2x02)(Aa2+B)xt−12−2(Aaxt+Bbx0)xt−1+(Axt2+Bb2x02)
我们记C=Aa2+BC=Aa^2+BC=Aa2+B,D=Aaxt+Bbx0D=Aax_t+Bbx_0D=Aaxt+Bbx0,K=Axt2+Bb2x02K=Ax_t^2+Bb^2x_0^2K=Axt2+Bb2x02
则
E=Cxt−12−2Dxt−1+KE=Cx_{t-1}^2-2Dx_{t-1}+KE=Cxt−12−2Dxt−1+K
然后进行二次配方:
Cxt−12−2Dxt−1=C[xt−12−2DCxt−1]=C[(xt−1−DC)2−(DC)2]Cx_{t-1}^2-2Dx_{t-1}=C{\left[x_{t-1}^2-2\frac{D}{C}x_{t-1}\right]}=C{\left[(x_{t-1}-\frac{D}{C})^2-\left(\frac{D}{C}\right)^2\right]}Cxt−12−2Dxt−1=C[xt−12−2CDxt−1]=C[(xt−1−CD)2−(CD)2]
故
E=C(xt−1−DC)2+(K−D2C)E=C\left(x_{t-1}-\frac{D}{C}\right)^2+\left(K-\frac{D^2}{C}\right)E=C(xt−1−CD)2+(K−CD2)
将所有我们定义的符号换回原符号:
{C=Aa2+B=(1−αˉt−1)αt+βt=αt−αˉt+βt=1−αˉtD=Aaxt+Bbx0=(1−αˉt−1)αtxt+βtαˉt−1x0\begin{cases} C=Aa^2+B=(1-\bar{\alpha}_{t-1})\alpha_t+\beta_t=\alpha_t-\bar{\alpha}_t+\beta_t=1-\bar{\alpha}_t \\D=Aax_t+Bbx_0=(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}}x_0 \end{cases}{C=Aa2+B=(1−αˉt−1)αt+βt=αt−αˉt+βt=1−αˉtD=Aaxt+Bbx0=(1−αˉt−1)αtxt+βtαˉt−1x0
即我们可以将该式子写成这样的形式:
[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]/(1−αˉt)β~t=E/Cβ~t=(xt−1−DC)2+(KC−D2C2)β~t\begin{aligned} &\frac{[(x_t-\sqrt{\alpha_t}x_{t-1})^2(1-\bar{\alpha}_{t-1})+(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2\beta_t]/(1-\bar{\alpha}_t)}{\tilde{\beta}_t} \\=&\frac{E/C}{\tilde{\beta}_t} \\=&\frac{\left(x_{t-1}-\frac{D}{C}\right)^2+\left(\frac{K}{C}-\frac{D^2}{C^2}\right)}{\tilde{\beta}_t} \end{aligned}==β~t[(xt−αtxt−1)2(1−αˉt−1)+(xt−1−αˉt−1x0)2βt]/(1−αˉt)β~tE/Cβ~t(xt−1−CD)2+(CK−C2D2)
其中(KC−D2C2)\left(\frac{K}{C}-\frac{D^2}{C^2}\right)(CK−C2D2)这一项是常数项,结果以及很明显了,我们的μ~(xt,x0)=DC=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxt\tilde{\mu}(x_t,x_0)=\frac{D}{C}=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_tμ~(xt,x0)=CD=1−αˉtαˉt−1βtx0+1−αˉtαt(1−αˉt−1)xt
现在我们已经得出去噪过程的均值和方差(为了下一步计算损失函数做准备):
{β~t=1−αˉt−11−αˉtβtμ~(xt,x0)=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxt\begin{cases} \tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t \\\tilde{\mu}(x_t,x_0)=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t \end{cases}{β~t=1−αˉt1−αˉt−1βtμ~(xt,x0)=1−αˉtαˉt−1βtx0+1−αˉtαt(1−αˉt−1)xt
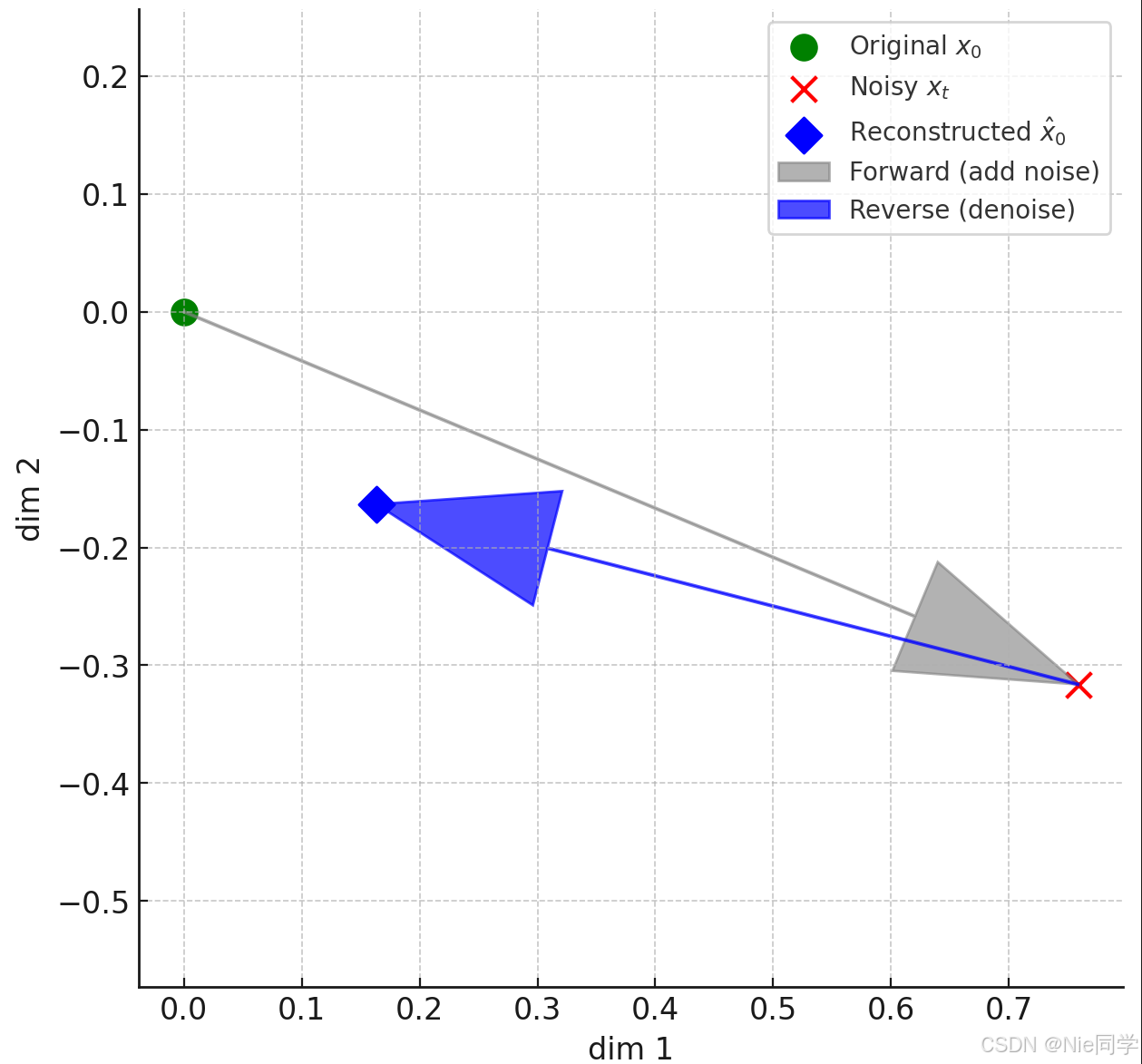
我们在第一步加噪阶段曾经定义过:
xt=αˉtx0+1−αˉtε,ε∼N(0,I)x_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\varepsilon,\quad\varepsilon\sim\mathcal{N}(0,\mathbf{I})xt=αˉtx0+1−αˉtε,ε∼N(0,I)
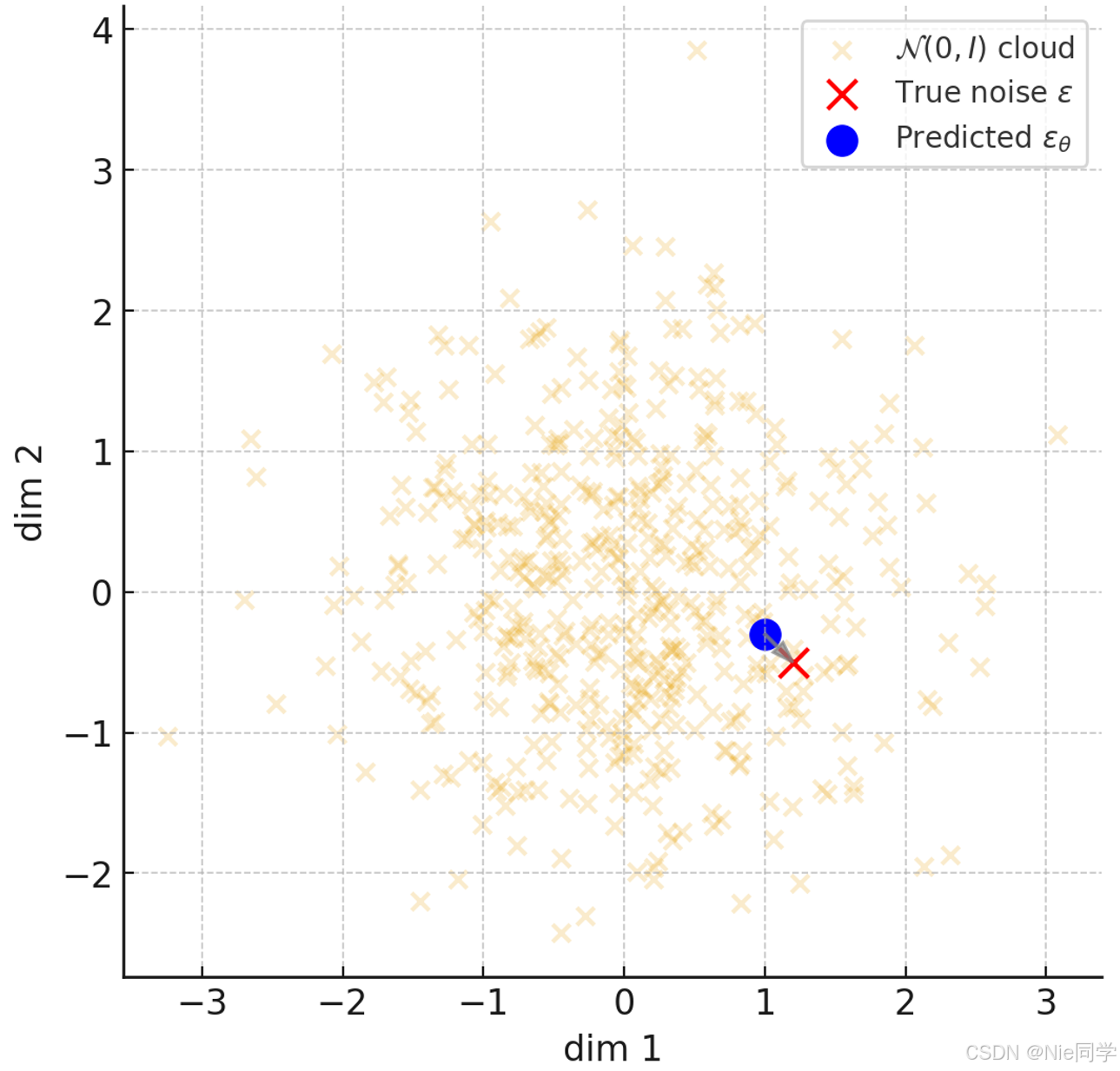
那么我们把最终x0x_0x0的生成用我们的预测噪声(εθ(xt,t)≈ε\varepsilon_\theta(x_t,t)\approx\varepsilonεθ(xt,t)≈ε)来表达:
x^0(xt,x0)=1αˉt(xt−1−αˉtεθ(xt,t)))\widehat{x}_0(x_t,x_0)=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t}\varepsilon_\theta(x_t,t)\right))x0(xt,x0)=αˉt1(xt−1−αˉtεθ(xt,t)))
网络只需猜中这一步注入的高斯噪声ε\varepsilonε即可得到x^0\widehat{x}_0x0,再喂入解析式后验得到反向均值(给定xtx_txt和x0x_0x0时,xt−1x_{t-1}xt−1的条件期望)一步“往回走”时的最可能位置。
网络预测εθ(xt,t)\varepsilon_\theta(x_t,t)εθ(xt,t)就是在标准高斯分布里找出最接近“当时加的噪声样本”的点。
参考文献
[1] 扩散模型(Diffusion Model)详解:直观理解、数学原理、PyTorch 实现
[2] diffusion model 原理讲解 公式推导
[3] Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models