leetcode滑动窗口(C++)
目录
1.长度最小的子数组
2.无重复字符的最长子串
3.最大连续1的个数|||
4.将x减到0的最小操作数
5.水果成篮
6.找到字符串中所有字母异位词
7.串联所有单词的子串
8.最小覆盖子串
错误思路+错误代码:
正确思路+正确代码:
1.长度最小的子数组

某个子数组中的数字相和,结果为target,最小的子数组中有几个元素?(若无法达到target,则输出0)
1.暴力解法:把数组中所有的子数组情况全部统计出来,正好达到target值的子数组中,元素量最小的( 左右指针+相和操作->O(N^3) )
2.利用单调性,使用“同向双指针”优化(同向双指针即滑动窗口)
- 找准一个锚点(起点),搞一个sum出来,right往后走就直接在sum上相和,因为题目中说了数组中都是正整数,所以只要比target大或一样大就更新最小子数组长度min(以例1为例,target=7,子数组相加为8为12都行,但为了更少的元素所以直接保留算出8的子数组个数),比target小就继续,相和操作没了变成O(N^2)的时间复杂度
- 找出一段子数组后,锚点往后移,重复上面的操作;此时不要把right返回到锚点,直接在sum的基础上减去锚点右移(以例1为例,left++以后,sum减去2最后等于6),重复上一操作……,因为右指针不需要再回到锚点往右走了,所以变成O(N)的时间复杂度,最坏情况是right走到底,left也走到底(例如数组中所有元素都比target要大),也就进行了2n次移动操作,所以不要被2层循环嵌套欺骗了!
- 结束循环条件:right出了数组范围,最后一段区间的子数组被计算完毕,结束循环
- 极限情况:不可能达到target的情况,right不断相加,超出了数组范围还是比target小,直接返回0
- 总结:比target小进窗口(right往后走),比target大出窗口(left往后走)
题目中的单调性即相和只会越来越大,同向双指针即两个指针只会往同方向移动
滑动窗口像一个会变大变小的数组,且起始点与终止点会改变
该办法就是寻找等价情况的边界值,规避很多没必要的枚举行为


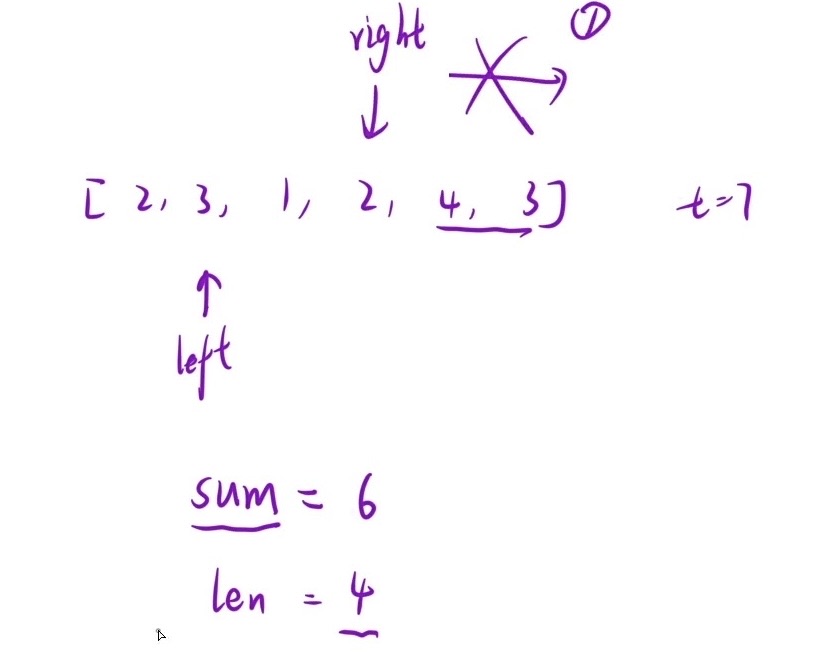
代码:
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int left, right;int sum = 0, min = INT_MAX;for (left = 0, right = 0;right <= nums.size() - 1;){while (right <= nums.size() - 1 && sum < target) sum += nums[right++];while (sum >= target){int len = right - left;if (len < min) min = len;sum -= nums[left++];}}if(min == INT_MAX) return 0;return min;}
};代码易错点:一定要在出窗口循环时更新啊!
如果不在出窗口循环时更新,当right出了数组以后,sum>=target时min就会一直为进窗口循环结束以后的结果
2.无重复字符的最长子串

子串:在字符串中的一个连续序列
所以题目要求的是:求出字符串中最长的一个无重复字符的连续序列

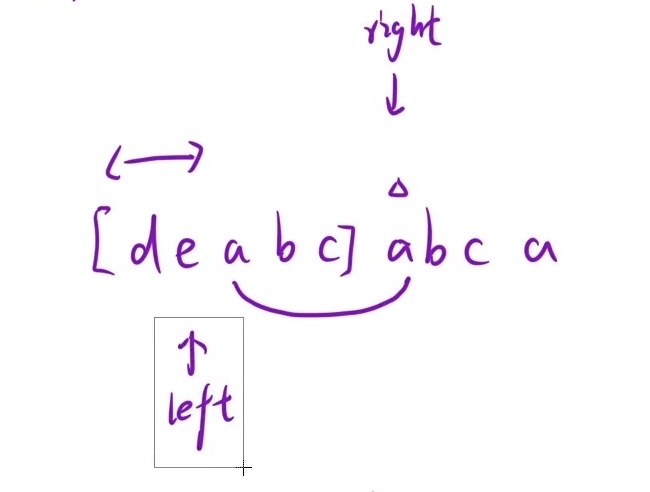
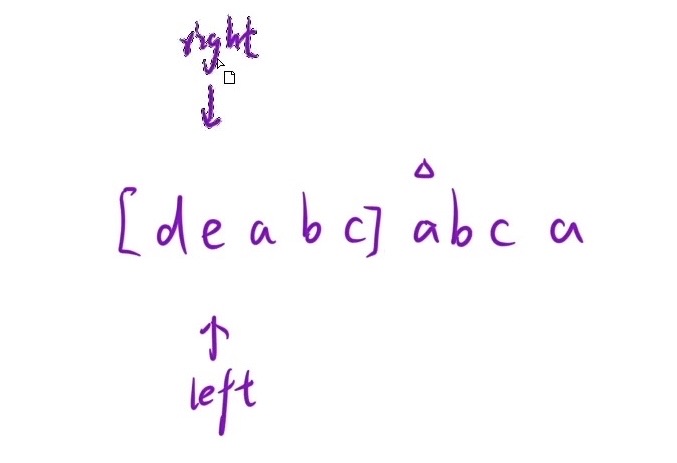
1.暴力解法:如上图,把所有没有重复字符的子串都枚举出来,找出所有子串中最长的那个;我们在判断重复字符时,可以通过hash表的方法(2层循环,O(N^2)的时间复杂度)
2.滑动窗口方法:right不要回去,因为子串是一个连续序列,right回到锚点(left位置)遍历一遍还是遍历到原来的位置,所以right没有回去的必要,只需让left移动从数组中出数据(如下图所示)
- 通过sum记录子串长度,通过max记录最长的子串长度
- hash表用一个int型数组来表示,字符的ascII码作为数组下标
- 结束循环条件:当right出了数组
- 极限情况:当字符串为空串时,直接返回0;当字符串只有一个字符时,该解法可以满足
代码:
class Solution {
public:int lengthOfLongestSubstring(string s) {int hash[130]={0};int left,right;int size=s.size();int max = 0;for(left=0,right=0;right<=size-1;){while(right<=size-1 && hash[s[right]] == 0) {hash[s[right]]++;right++;int len = right-left;if(len>max) max=len;}while(hash[s[right]]) {hash[s[left]]--;left++;}}return max;}
};3.最大连续1的个数|||

有个2进制数组,里面的0可以从0翻转成1,至多翻转k个0(可以翻转0个、1个、……、k个)之后,求出最长的连续1个数
1.转化:不要真的去翻转0!!!只要在一段只有0和1组成的子数组中,0的数量不大于k,就相当于翻转0以后的结果
2.滑动窗口的思想:子数组中0的数量小于等于k,right往后走;子数组中0的数量大于k,left往后走;len记录长度,max记录最长的子数组长度,sum_0为0的个数;极限情况下( nums.length = 1),这种办法也完全能解决;right走出数组,结束循环,因为left往后子数组长度只会越来越小
代码:
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int size = nums.size(), left, right, max = 0;int sum_0 = 0;for (left = 0, right = 0;right <= size - 1;){while (right <= size - 1 && sum_0 <= k){if (!nums[right]){sum_0++;right++;}else right++;if (sum_0 <= k && right - left > max) max = right - left;}while (sum_0 > k){if (nums[left] != 0) left++;else{left++;sum_0--;}}}return max;}
};代码易错点:实际考试时一定要宁可多写点代码,不要省略!!!
笔者就因为if-else语句的括号没有好好加,调试了半天才发现问题,快就是慢,慢就是快,一切都以把题目ac为导向
另要注意:
if (sum_0 <= k && right - left > max) max = right - left;
因为外面一层循环的判断是发生在 max = right - left后,所以有可能sum_0已经比k大了,但依旧还没有出循环
4.将x减到0的最小操作数

每次操作只能删除数组最左边or最右边的元素,从x中减去该元素的值,达到目的所需要的最小操作数
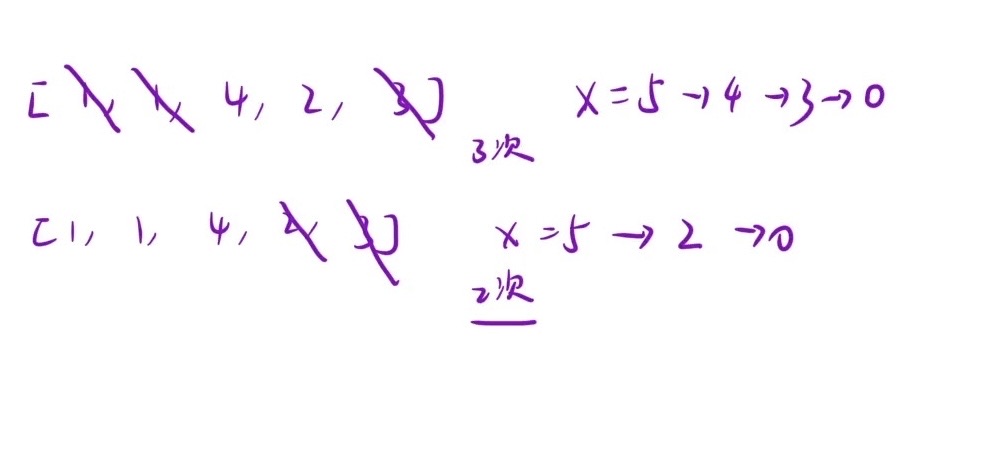
1.转换:直接做太难了,有时候要删左边,有时候要删右边,删哪边是不确定的;所以要通过正难则反的思想来简化这道题目,把数组中所有元素相加,减去x值以后就是数组余下元素的和sum,那么现在只需要求出和为sum的子数组,此时操作数即数组元素个数减去子数组元素个数
2.滑动窗口:
操作数要最少,那么子数组要最长,即通过滑动窗口的办法求出和为sum-x的最长子数组
当子数组的和大于sum-x,left++(出窗口);当子数组的和小于sum-x,right++(进窗口);当子数组的和等于sum-x时,更新操作数次数,同时left++
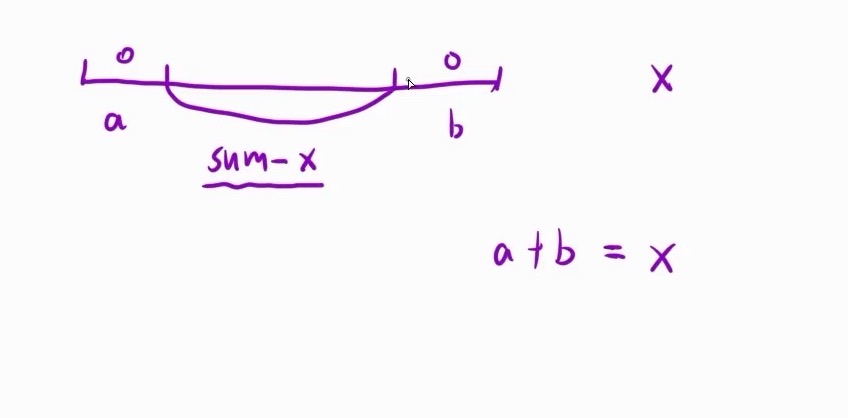
代码:
class Solution {
public:int minOperations(vector<int>& nums, int x) {int sum = 0 ;for(auto i:nums) sum+=i;int flag = sum - x;if(flag<0) return -1;if(flag == 0) return nums.size();int size=nums.size(),left,right,max=0,add=0;for(left=0,right=0;left<=size-1,right<=size-1;){while(right<=size-1 && add<flag) add+=nums[right++];while(left<=size-1&&add>=flag){if(add == flag) {if(right-left>max) max = right-left;}add-=nums[left++];}}if(!max) return -1;return size-max;}
};
代码易错点1:flag(sum-x)如果是个负数,add > flag恒成立,会陷入while(add>flag)的死循环,所以需要注意
我的解决办法:当flag是个负数时,怎么可能加出来一个负数呢?因为不可能实现,所以直接返回-1
代码易错点2:当数组中所有数相加起来结果为x,即flag == 0;此时没有一种方式可以相加出0,所以需要考虑到这个情况
我的解决办法:直接返回整个数组的元素即可
5.水果成篮

i 棵树,fruits[i]表示第 i 棵果树的水果种类,只有2个篮子且每个篮子只能装单一类型的水果;可以选择从任意一棵树开始摘,每棵树摘完1颗向右移动并继续采摘,一旦走到某棵树前,2个篮子都不能装,停止采摘。现在要求2个篮子可采摘水果数量的最大值。
1.转化:找出一个最长的子数组长度,数组中只能有2种数字
2.left++时数字种类只会不变or变小,可以用出窗口的思想;right++时数字种类只会不变or变大,可以用进窗口的思想。综上所述,使用滑动窗口来解决。
搞一个哈希表来记录水果种类,当hash.size()>2时出窗口,当hash.size()<=2时进窗口
代码:
class Solution {
public:int totalFruit(vector<int>& fruits) {int left,right,size=fruits.size(),max=0;unordered_map<int,int> hash;for(left=0,right=0;right<=size-1;){while(right<=size-1 && hash.size()<=2) {hash[fruits[right]]++;right++;if(hash.size()<=2 && right-left>max) max=right-left;}while(hash.size()>2){hash[fruits[left]]--;if(!hash[fruits[left]]) hash.erase(fruits[left]);left++;} }return max;}
};代码易错点:在一个键为时,记得从hash表中删除该键值对,要不然hash表中一直会保留着该键值对,hash表的size大小就会出问题
if(!hash[fruits[left]])
hash.erase(fruits[left]);
6.找到字符串中所有字母异位词

异位词:2个字符串所含有的字符相同,字符顺序任意
找出 s 中所有 p 的异位词子串,返回这些子串的起始下标,不考虑输出顺序
1.如何快速判断两个字符串是否是异位词?
借助哈希表来统计两个字符串的字符构成,如果字符构成完全一致,那么就互为异位词
2.滑动窗口解法:
第一次判断时,直接从 s 中划出 p 字符个数的子串,然后窗口一进一出就可以确保两个字符串的字符个数肯定相同(相当于把窗口整体往右移动一格,如下图所示)
每次进窗口,出窗口判断一次hash表中的字符构成,如果相同就返回起始下标,不同就继续
最后,如果出现了 s字符串大小 比 p字符串大小 还要小,那么可以直接返回一个空数组,因为 s 中不可能存在一个子串和 p 互为异位词
3.如何使用两个hash表来判断异位词呢?
搞两个数组 int hash[26] 来模拟哈希表,每次判断也只需要循环26次即可,只要对应字母数量相同,那么就算互为异位词
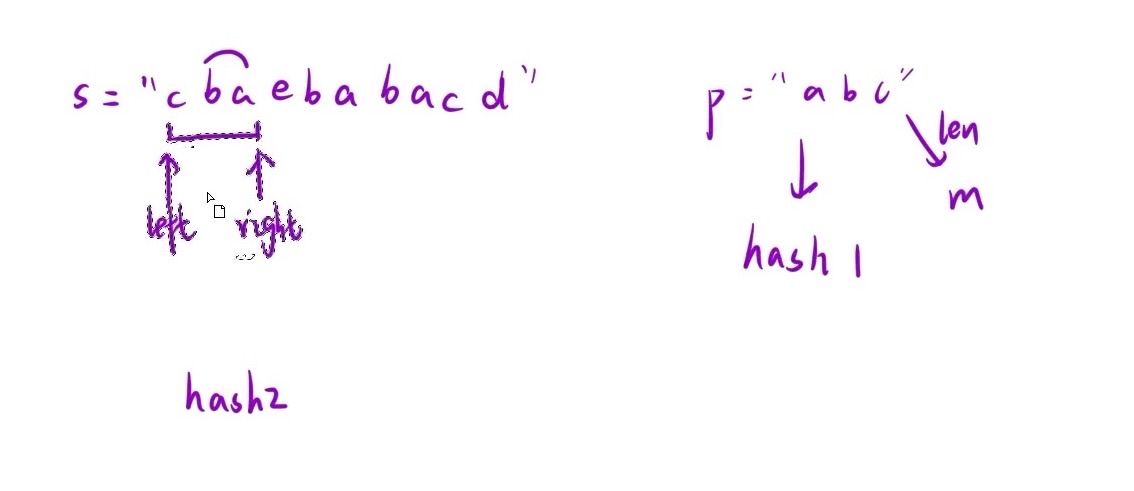

代码:
class Solution {bool check(vector<int>& hash1,vector<int>& hash2){for(int i=0;i<=25;i++)if(hash1[i]!=hash2[i]) return false;return true;}
public:vector<int> findAnagrams(string s, string p) {if(s.size()<p.size()) return {};vector<int> hash1(26,0);vector<int> hash2(26,0);vector<int> ret;for(auto i:p) hash2[i-'a']++;int left=0,right=0;for(;right<=p.size()-1;right++) hash1[s[right]-'a']++;for(;right<=s.size()-1;left++,right++){if(check(hash1,hash2)) ret.push_back(left);hash1[s[left]-'a']--;hash1[s[right]-'a']++;}if(check(hash1,hash2)) ret.push_back(left);return ret;}
};代码优化:
check函数得要循环26次才能判断一次,会不会时间复杂度有点过高了?
所以我们就利用变量count来统计窗口中“有效字符”的个数
以此为例:s = "ccbeabcbacd" p="abc"
一开始,left和right都指向第一个元素,因为第一个元素为c,此时p中也有一个c,所以2个c就相当于可以抵消掉,此时可以把 s 中的第一个元素当作有效元素,count++;然后让right++(进窗口),此时又发现了一个c元素,但此时p中的元素c已经被抵消掉了,所以出现了一个无效元素,count不用再加1;重复该操作,直到 count = 3(即 p 的长度);此时left和right之间有2个c、1个b、1个a(4个字符),让left往后走(出窗口),直到left和right之间只有3个字符(p的长度),开始判断count是否为3(此时 count == 3,原因是把第一个c又被当作了无效字符,方法如下)
提问:如何将2个c抵消掉的同时不把多余的字符当作有效字符?
很简单,只要搞两个hash表,s 的为hash1, p 的为hash2
每次进窗口以后判断 hash1[in] <= hash2[in],如果进窗口以后的字符数量比p的同一字符数量小(或相等)就视为有效字符,count++
每次left和right之间的长度与 p 不相等时出窗口,当 "eabc" 出了一个 'e' 之后就是异位词了;所以我们需要每次出窗口前判断 hash1[out] <= hash2[out],如果满足就视为有效字符被舍去了,因此count--;hash2里 'e' 下标的值为0 ,hash1里 'e' 下标的值为1,count不需要减去1,所以此时count依旧为3,不会漏掉结果;"ccbea"依旧是这样,第一个count不减1,第二个count要减1,因此bea不会被统计进结果
优化代码:
class Solution {
public:vector<int> findAnagrams(string s, string p) {if(s.size()<p.size()) return {};vector<int> hash1(26,0);vector<int> hash2(26,0);vector<int> ret;int count = 0;for(auto i:p) hash2[i-'a']++;for(int left=0,right=0;right<=s.size()-1;right++){//进窗口hash1[s[right]-'a']++;//进窗口判断if(hash1[s[right]-'a']<=hash2[s[right]-'a']) count++;//长度判断while(right-left+1>p.size()){//出窗口判断if(hash1[s[left]-'a']<=hash2[s[left]-'a']) count--;//出窗口hash1[s[left]-'a']--;left++;}//结果判断if(right-left+1 == p.size() && count == p.size()) ret.push_back(left);}return ret;}
};
我们是冠军!!!
7.串联所有单词的子串

如果 words = ["ab","cd","ef"], 那么 "abcdef", "abefcd","cdabef", "cdefab","efabcd", 和 "efcdab" 都是words的串联子串
返回所有串联子串在 s 中的起始下标,可以以任何顺序返回答案,words 中所有字符串长度相同
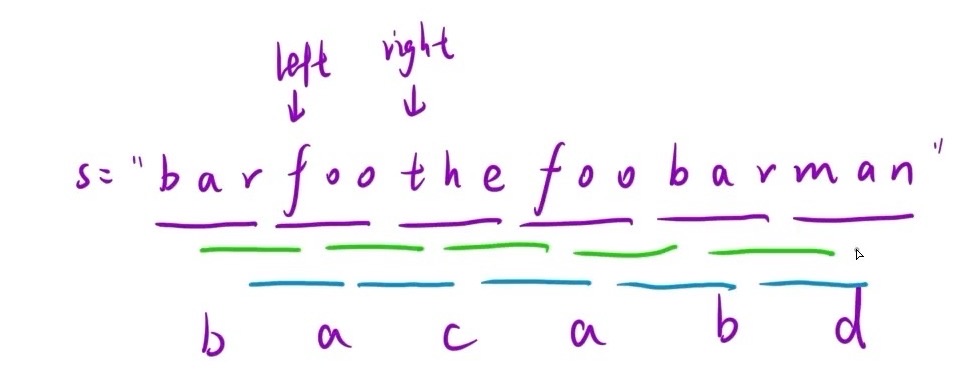
本题是基于上题的进阶,(以例一为例)可以把foo视为a,把bar视为b,其他的就小写字母表中的顺序排列,那么题目就变成了从 "bacabd" 中找出 "ab" 的异位词子串
该题有3个难点:1.怎么把字符串作为元素存进哈希表;2.left和right该怎么移动;3.滑动窗口应该怎么执行
- 问题1:可以创建一个hash表,类型为 hash<string,int> ;每次存入的字符串通过 c++ 自带的 substr() 函数截取,每次截取 words.size() 个
- 问题2:left、right都应该以 words.size() 个字符为单位移动
- 问题3:重点重点重点!!!如下图所示(例一),以首字符为起点进行遍历以后(即bar、foo、the、……),还能再以第二个字符为起点进行遍历(即arf、oot、hef、……);截止到第4个字符f,因为第4个字符遍历出来的情况就是第一种去掉了开头的bar
代码:
class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {vector<int> ret;unordered_map<string,int> hash1;int size = words[0].size();int size_sum = size*words.size();if(s.size()< size_sum) return {};for(auto& sos : words) hash1[sos]++;//整体for(int i=0;i<=size-1;i++){unordered_map<string,int> hash2;int count = 0;//单趟for(int left=i,right=i;right+size<=s.size();right+=size){//进窗口+添加有效字符串的判断string in = s.substr(right,size);hash2[in]++;if(hash2[in] <= hash1[in]) count++;//长度判断while(right-left+1 > size_sum){//出窗口+删除有效字符串的判断string out = s.substr(left,size);if(hash2[out]<=hash1[out]) count--;hash2[out]--;left+=size;}if(count == words.size()) ret.push_back(left);}}return ret;}
};代码易错点:
- 统计字符的哈希表与统计有效字符的count需在整体的循环内创建,如此才能每次单趟判断互相之间不影响(上一次hash表存放的结果,会导致下一次判断有效字符时出现问题)
- 单趟的退出条件为 right + size <= s.size() ,要不然就会导致substr的时候超出字符串截取(例如例一,……an 从 a 开始 substr 那么就会超出字符串范围,an也不可能作为答案,因此直接停止循环即可)
- 在存放结果判断前,不要加上 right - left + 1 == size_sum ;以例一为例当 count == 2时,right 还指向了 foo 的 'f' , 此时如果再加上这个判断条件,那么就会一个结果也存放不进去
8.最小覆盖子串

从 s 中找出一个子串,要求子串覆盖 t 中所有的字符,同时字符数量最少
错误思路+错误代码:
该题思路和前两题有重合,count来统计是否满足覆盖条件,hash表来统计字符数量
区别点:
- 出窗口结束条件要变成 right - left < 当前最短子串长度
- 每次判断完更新结果时,要将right、left下标保存下来,以便于最后的返回
- 每次left往后移动前,不要着急出窗口,可以等到 left 移动到了某一个存在于 t 中字符再终止,因为别的字符为起点的一定不是最短子串(例一为例,"eabc" 和 "abc")
- 键值对不存在,unordered_map的count函数给出的返回值不是0!!!
class Solution {
public:string minWindow(string s, string t) {string ret;if(s.size()<t.size()) return ret;vector<int> hash1(150,0);vector<int> hash2(150,0);int len_min = INT_MAX;int left_min = -1, right_min = -1,count = 0;int left,right;for(auto x:t) hash1[x]++;for(left=0,right=0;right<=s.size()-1;right++){//进窗口+有效字符添加判断char in = s[right];hash2[in]++;if(hash2[in]<=hash1[in]) count++;//left提前移位while(left <= s.size()-1 && !hash1[s[left]]) left++;//出窗口+有效字符删除判断while(count == t.size() && right - left + 1 >= len_min){char out = s[left];if(hash2[out]<=hash1[out]) count--;hash2[out]--;left++;}//更新结果if(count == t.size()){left_min = left;right_min = right;len_min = right-left+1;}}if(right_min == -1) return ret;ret = s.substr(left_min,right_min-left_min+1);return ret;}
};
笔者在尝试了9981个小时后,发现把left移动到存在于 t 中的字符上来解决问题不太可行,因此换成了下面的方法
正确思路+正确代码:
- 不同于错误思路(窗口不合法,出窗口操作完毕后再判断),现在选择窗口刚合法时出窗口,出窗口前先判断是否需要更新结果,不断出窗口直至窗口从合法变为不合法
- 每次更新,更新结果的起始位置与最短长度,不记录结果的截止位置
- 其他思路不变
class Solution {
public:string minWindow(string s, string t) {int hash1[128] = {0};for(auto ch:t) hash1[ch]++;int hash2[128] = {0};int len_min = INT_MAX,start = -1;for(int left=0,right=0,count=0;right<=s.size()-1;right++){//进窗口char in = s[right];hash2[in]++;if(hash2[in]<=hash1[in]) count++; //统计有效字符个数//判断窗口是否合法while(count == t.size()){//判断是否需要更新结果if(right - left + 1 < len_min){len_min = right - left + 1;start = left;}//出窗口char out = s[left++];if(hash2[out]<=hash1[out]) count--;hash2[out]--;}}return start == -1 ? "" : s.substr(start,len_min);}
};思路错误与正确的原因:
- 错误原因在于left即使提前移位了,依旧会移位到hash1中存在的无效字符上,结果无法作为最优解存在;同时,如果想要后续通过left后移判断更新结果,那么就会导致各种报错,因此放弃该思路
- 正确原因在于每次刚刚合法就开始判断,每次出完一个窗口判断一次,而不是全部出完以后再进行判断,更好地完成了left移位判断操作
