【区块链学习笔记】16：以太坊中的交易树和收据树

交易树（Transaction Tree）和收据树（Receipt Tree）

每个交易执行完会得到一个收据，记录这个交易的相关信息，以太坊把这些收据也组织在一起形成了一棵收据树。收据树和交易树上的节点是一一对应的，有利于智能合约快速查询交易的结果。

它们和状态树和区别

以太坊里三棵树数据结构用的都是MPT（相比于比特币的普通Merkel Tree，能支持查找操作）。 对状态树查找的key就是账户的地址。对交易树和收据树和交易树查找的key是交易在发布的区块中的序号（交易的排列顺序是由发布区块的那个节点决定的）。

交易树和收据树都是只把当前发布的区块里的交易组织起来的，而状态树则组织的是以太坊系统中所有账户的状态。

交易树是共享节点的，只有修改的那些账户会有新子树。而交易树和收据树每次新发布区块都是独立的全新的，不共享任何节点。

有什么用？

提供Mrkel Proof，像比特币一样，可以用来证明某个交易被打包在某个区块里（在收据树里则还能证明某个交易的执行结果）。

以太坊还支持一些比较复杂的查询，如找过去十天当中所有和某个智能合约有关的交易、所有众筹事件、所有发行新币的事件。。如果不做优化，只能把过去十天的所有区块都查一遍，从里面手动过滤。这种方法复杂度高，而且对轻节点（只有块头）很不友好。

Bloom Filter

为了能支持这些复杂查询操作，以太坊引入了布隆过滤器。每个交易执行完得到的收据里有一个BF，记录这个交易的类型、地址等信息。发布的区块在块头里也有个总的BF，是这个交易里所有区块的BF的并。

所以如果要查询过去十天所有某种类型的交易（比如众筹），就可以遍历过去十天的区块，先看看它们的BF里哪些包含想要的类型的交易（BF有可能False Positive但是不会False Negative，所以块头里都没有就一定可以无视），如果块头里有，再去交易树里查看看哪些交易里有（也一样可能False Negative），最后再找对应的那些交易进行确认。

好处是通过BF的结构能快速过滤大量无关的区块和交易，对少数的候选区块和交易再double check。

以太坊的运行过程可以看作是交易驱动的状态机（tx-driven state machine）。其实比特币也可以看作是交易驱动的状态机，驱动的状态就是UTXO（没有被花掉的那些交易集合），每次交易都会从UTXO里用掉一些交易，又会新加一些交易。而且这个状态机一定是确定性的（对于给定的状态和给定的一组交易，能够确定性的转移到下一个状态），因为所有的矿工都要进行一样的状态转移。

新创建的账户怎么收款？

如果有一笔交易，目标账户是一个完全没出现过的地址，这是有可能的，因为以太坊和比特币一样创建账户只要在本地生成就行了。只有账户第一次收到钱的时候，其他的节点才会知道这个账户的存在，这个时候要在状态树中新插入一个账户地址。

能不能把状态树也设计成只包含发生交易的账户的状态？

这样的话每个区块都只包含发生交易的那一点账户，没有完整的所有账户的信息，如果有一个A-(10 ETH)->B的交易，要检查A的账户里有没有10个ETH，那么可能要往前找很多很多节点，才能找到包含A这个账户状态树的节点（如果A很长一段时间没有发生交易的话）。

还有一个更大的问题，还要找B的账户里有多少ETH，才能把10个ETH加上来得到新的账户状态。但是如果B是一个新创建的账户怎么办？那么这种设计下要找到创世纪块才会发现B是一个新创建的账户，非常浪费算力。

数据结构代码解读

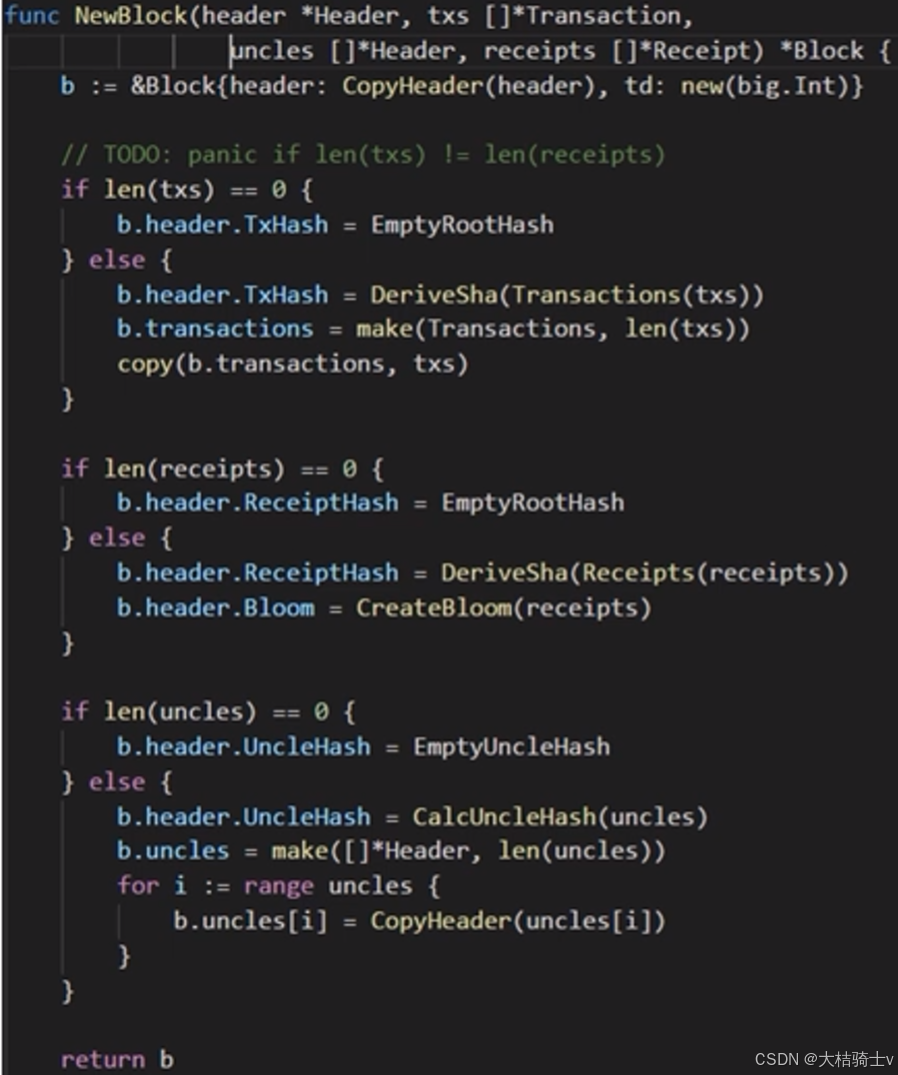
创建交易树时，判断交易列表（txs）是否为空，空就直接置空对应的树根哈希，否则计算它们的根哈希（调用DeriveSha）写到b.header对应的块头里，并把交易列表copy到区块b里去。

创建收据树时，判断收据列表（receipts）是否为空，空就直接置空对应的树根哈希，否则计算它们的根哈希（调用DeriveSha）写到b.header对应的块头里，并用CreateBloom计算块头的BF（由这个区块的所有收据的BF计算得到）。

最后一段则是设置叔父区块列表的。

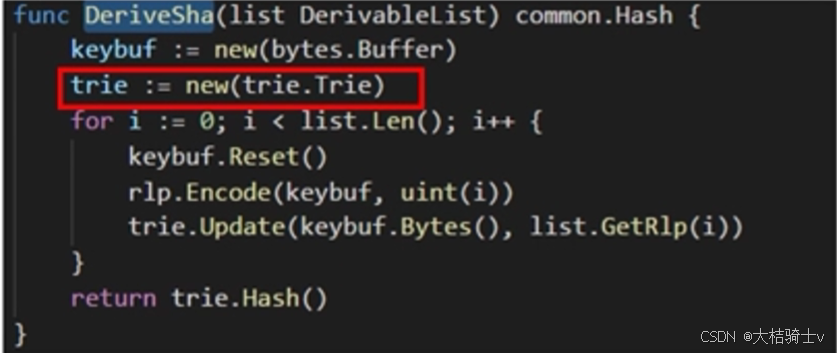
这哪里有树？在DeriveSha的时候会创建MPT，然后用RLP编码并写入进去，再计算的哈希：

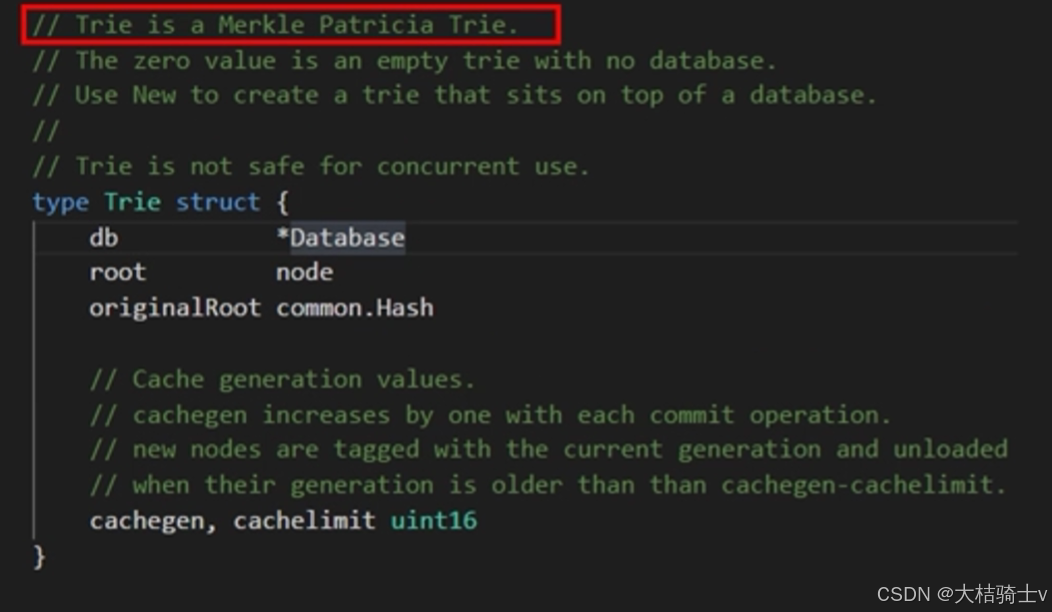
虽然命名是Trie，实际是MPT：

每个交易对应的收据的数据结构，其中Bloom就是根据Logs产生出来的：

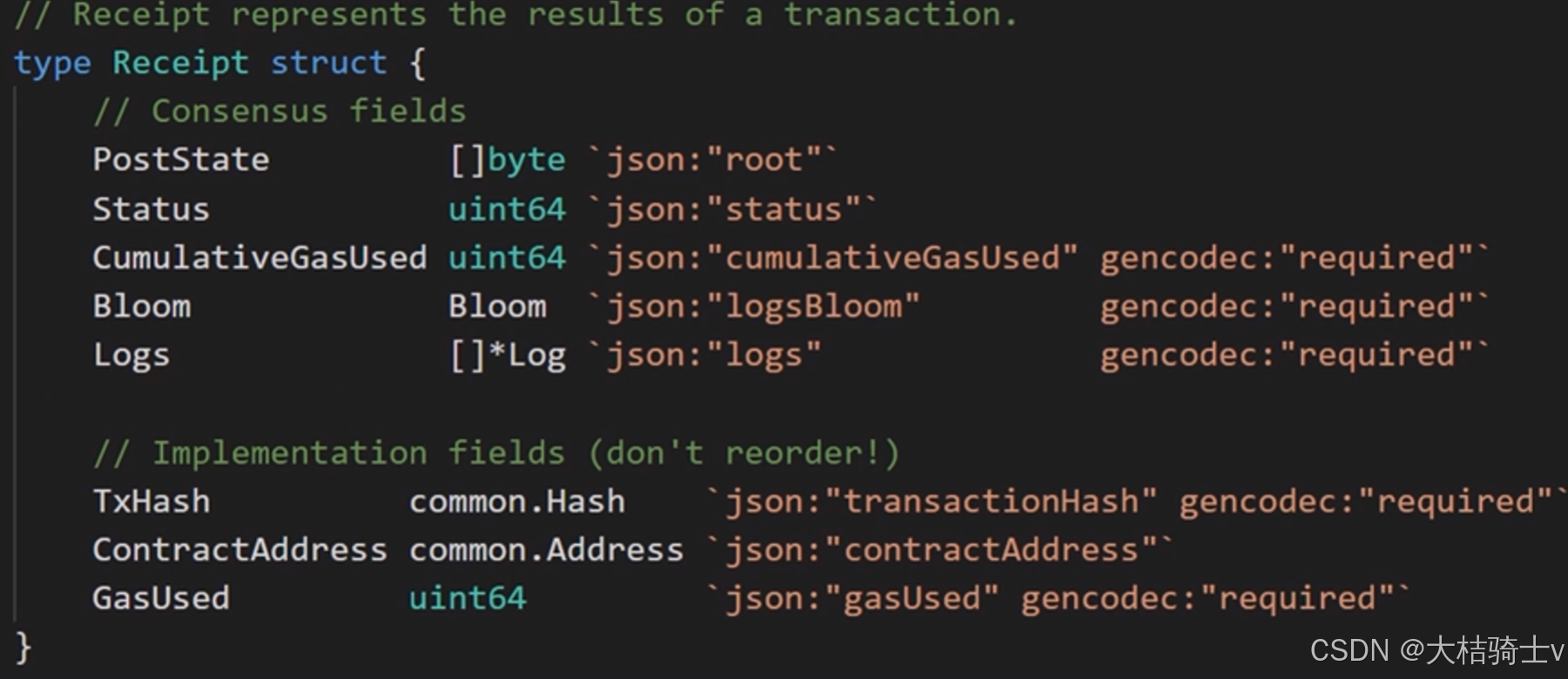
BF相关代码解读

CreateBloom用来创建整个区块的BF（放在块头里），它是由每个收据的BF合并在一起（Or）得到的，它的参数就是这个区块里的所有收据。

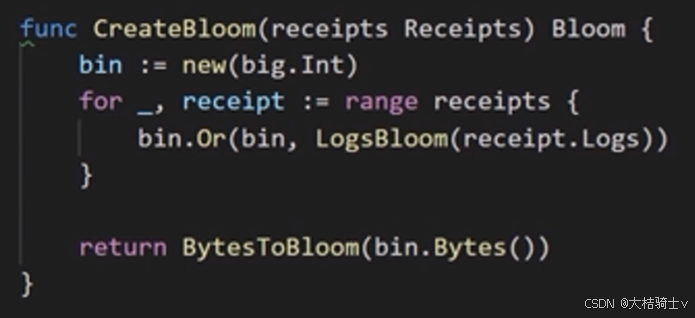
LogsBloom用来生成每个收据的BF，参数是收据的Log数组，每个Log的地址和Topic都会被Or进BF里，形成整个收据的BF。

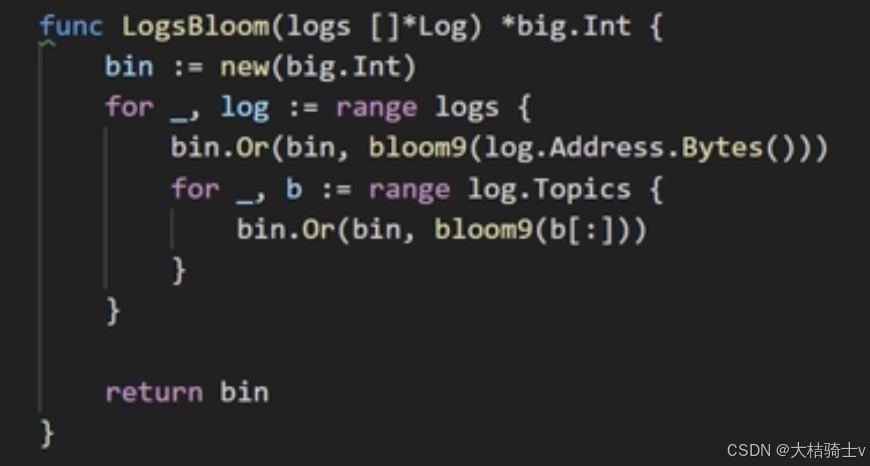
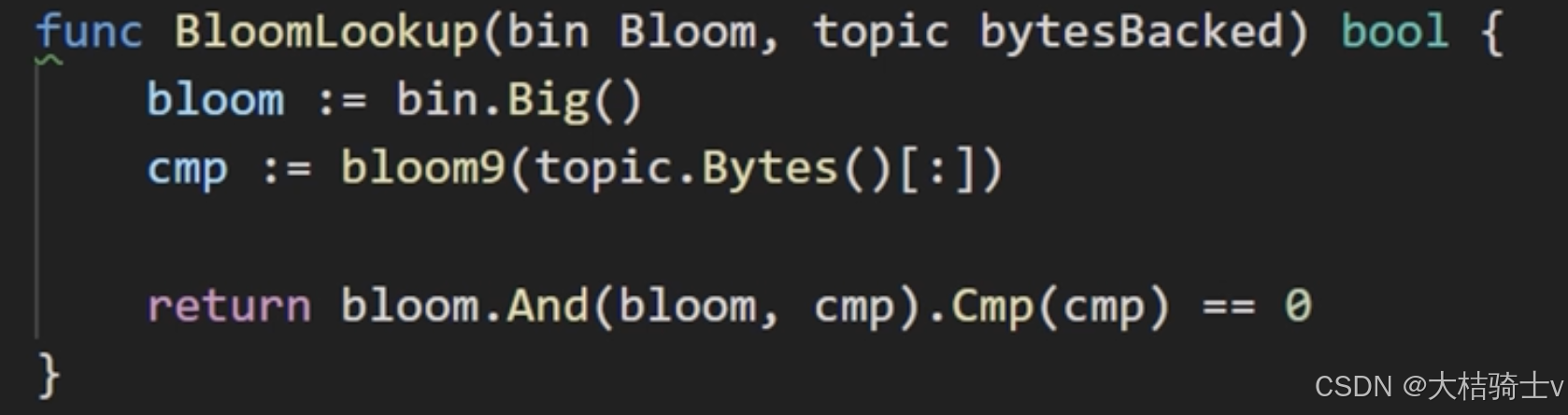
bloom9是BF所使用的哈希函数，第一行得到的b是256位32个字节的哈希值，然后将哈希值取前6个字节，每两个一组拼接在一起（分别作为16bit数的高低8位），然后与上2047（也就是对2048取余，相当于截断末尾11位数，得到0～2047这个区间里的树，之所以要这么干是因为以太坊里BF的长度是2048位），然后将1左移这么多位，然后Or到结果的BF里（也就是变量r）。从这个过程可以看出，以太坊的BF是2048 bit的桶，每个元素得到的是桶里的（至多）3个位置，BF操作会把这三个位置置为1。

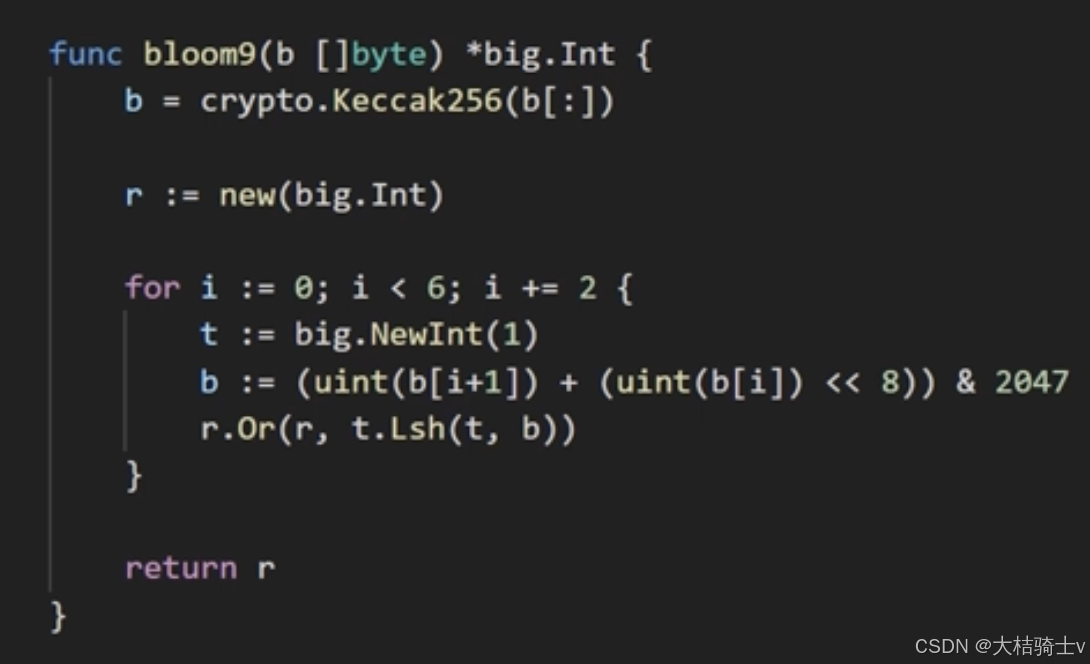
当要查询某个感兴趣的Topic是不是在指定的BF里时，只要转成BF然后与一下看看对应的位置是否是1（和BF相与不变）即可：