【算法训练营Day30】动态规划part6

最长连续递增序列

题目链接：674. 最长连续递增序列

解题思路：

使用dp数组记录当前下标的连续递增序列的长度即可

解题代码：

class Solution {public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];dp[0] = 1;int max = 1;for(int i = 1;i < nums.length;i++) {if(nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;else dp[i] = 1;if(dp[i] > max) max = dp[i];}return max;}
}

最长递增子序列

题目链接：300. 最长递增子序列

解题逻辑：

本题引入了子序列的概念，与上一题的区别在于：上一题是连续的递增序列，而本题是递增的子序列不一定连续。既然是要用dp，那么就要把问题拆成多个重叠的子问题，在上一题中我们是根据当前元素的前一个元素进行递推，而本题因为子序列不具有连续性，那么我们就要根据当前元素之前的递增子序列进行递推。

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i]表示以i结尾的最长递增子序列长度。
• 递推式：dp[i] = max(dp[j] + 1, dp[i])
• 初始化：所有元素初始化为1
• 遍历方向：从左至右

解题代码如下：

class Solution {public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];for(int i = 0;i < nums.length;i++) dp[i] = 1;int max = 1;for(int i = 1;i < nums.length;i++) {for(int j = 0;j < i;j++) {if(nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);if(dp[i] > max) max = dp[i];}}}return max;}
}

最长重复子数组

题目链接：718. 最长重复子数组

解题逻辑：

本题是将两个数组比较的所有状态给存储起来，然后根据状态来进行递推。

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示以i - 1指向的nums1数组尾部与j - 1指向的nums2数组尾部，形成的最长重复子数组长度。
• 递推式：if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1
• 初始化：所有元素初始化为0
• 遍历方向：两层for循环都是从左至右

为什么dp[i][j]表示以i - 1指向的nums1数组尾部与j - 1指向的nums2数组尾部形成的最长重复子数组长度，而不是以 i 指向的nums1数组尾部与 j 指向的nums2数组尾部形成的最长重复子数组长度？

如果是这样的话，我们的递推公式是if(nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1

我们以一个4 * 4的矩阵来看的话：

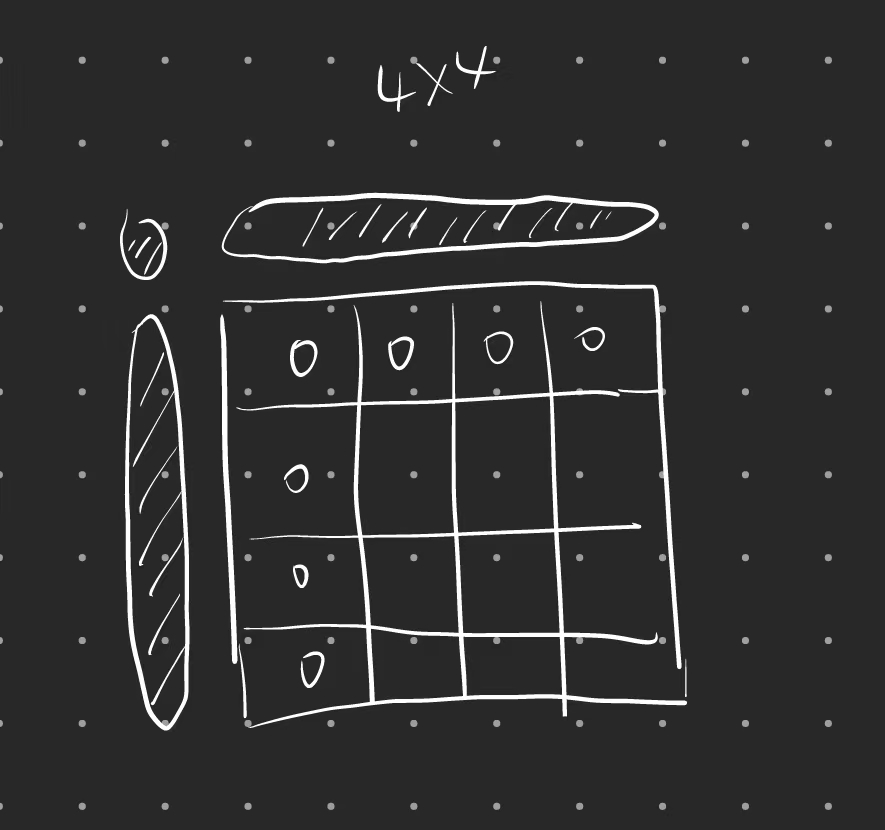
我们在处理第一行以及第一列的递推时会出现越界的情况，所以这种情况下要进行一些复杂的初始化操作。那么我们的理想状态就是拥有这些阴影区域的数据，可以让我们完成第一行以及第一列的递推。那么我们干脆就把所有数据往里面缩一缩，从索引为1的行与列开始记录。如此我们的dp数组含义也要发生变化，故表示：dp[i][j]表示以i - 1指向的nums1数组尾部与j - 1指向的nums2数组尾部，形成的最长重复子数组长度。

class Solution {public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length + 1][nums2.length + 1];int max = 0;for(int i = 1;i <= nums1.length;i++) {for(int j = 1;j <= nums2.length;j++) {if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;if(dp[i][j] > max) max = dp[i][j];}}return max;}
}

最长公共子序列

题目链接：1143. 最长公共子序列

解题逻辑：

我们从dp四部曲来分析这个问题：

• dp数组含义：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]。
• 递推式：
  • i,j指向的字符相等：dp[i][j] = dp[i - 1][j - 1] + 1
  • i,j指向的字符不相等：dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);
• 初始化：所有元素初始化为0
• 遍历方向：从上到下，从左到右

其实这里的递推式初次看并不好理解。要想看懂的话先要理解动态规划的本质：将子问题的结果存储到数组中，然后根据子问题的结果推导原问题的结果。当i,j指向的字符相等：dp[i][j] = dp[i - 1][j - 1] + 1。这个递推式好理解，既然i,j指向的字符相等，那我们只需要得到i - 1，j - 1对应的最长公共子序列，然后 + 1就行。但是i,j指向的字符不相等：dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1])，这个递推式如何理解呢？既然现在i，j指向的字符不相等了，那么一起使用i与j指向的元素对最长公共子序列的值不会有增长效果，那么此时我们可以考虑继承其他情况的最长公共子序列的值。所以我们可以尝试舍弃掉i的最后一个字母，看一下i - 1，j 对应的最长公共子序列，或者舍弃掉j的最后一个字母，看一下i，j - 1对应的最长公共子序列，把他们之中较大的拿过来作为当前的最长公共子序列。

解题代码：

class Solution {public int longestCommonSubsequence(String text1, String text2) {int[][] dp = new int[text1.length() + 1][text2.length() + 1];int max = 0;for(int i = 1;i <= text1.length();i++) {for(int j = 1;j <= text2.length();j++) {if(text1.charAt(i - 1) == text2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);}}}return dp[text1.length()][text2.length()];}
}

子数组、子序列问题中dp数组定义与返回值套路总结

问题一：什么情况下是在dp数组中寻找最大值返回，什么情况下是直接将dp数组的最后一个值返回？

这个就需要严抓dp数组的定义，例如我们可以将最长公共子序列的dp数组含义与最长重复子数组的dp数组含义做一个对比：

• 长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
• dp[i][j]表示以i - 1指向的nums1数组尾部与j - 1指向的nums2数组尾部，形成的最长重复子数组长度

第一个囊括了之前的所有状态，而第二个只保存了以当前字符结尾的状态，所以前面的只需要将dp数组的最后一个值返回，而第二个则需要寻找最大值。

问题二：dp[i][j]的含义什么时候代表以i-1和j-1结尾，什么时候代表[0,i-1]和[0,j-1]?

• 定义 1：dp[i][j] 代表以 s1[i-1] 和 s2[j-1] 结尾的目标值

  • 使用场景：当问题要求子序列 / 子串必须连续（如最长公共子串），或必须包含最后一个字符时，通常用这种定义。
  • 特点：强调结尾限制（不关注从哪开始）：子序列 / 子串必须包含 s1[i-1] 和 s2[j-1] 这两个字符，且以它们为最后一个字符。
  • 核心逻辑：通过强制包含结尾字符，将问题拆解为前序部分的解 + 当前字符的贡献。
  • 获取结果的方式：一般通过遍历获取最大值

• 定义 2：dp[i][j] 代表s1[0…i-1] 和 s2[0…j-1] 范围内的目标值

  • 使用场景：当问题允许子序列不连续（如最长公共子序列），或不要求包含最后一个字符时，通常用这种定义。
  • 特点：强调范围限制：不要求包含最后一个字符，只考虑两个字符串的前 i 和前 j 个字符范围内的最优解（可能包含也可能不包含 s1[i-1] 或 s2[j-1]）。
  • 核心逻辑：范围性的最优解可能包含或不包含结尾字符，因此需要综合两种情况（包含 / 不包含）取最优。
  • 获取结果的方式：一般直接取dp数组的末尾值即可

从正面来说这些概念不痛不痒，我们举一个反例会理解的更深刻。例如我们在最长公共子序列这个问题中，我们将dp[i][j]定义为以i - 1指向的字符串尾部与j - 1指向的字符串尾部，形成的最长公共子序列长度。那么我们随便写一个阶段的递推公式，例如:text1[2] == text2[3]，那么dp[3][4] = dp[2][3] + 1； 把这个递推式翻译一下：以2结尾的text1和以3结尾的text2形成的最长公共子序列长度等于以1结尾的text1和以2结尾的text2形成的最长公共子序列长度加上1。要知道以什么结尾这种定义方式结尾是必须要包含的，那么相当于前后相连了，这其实求的是最长重复子串。

不相交的线

题目链接：1035. 不相交的线

和上一题的解题逻辑基本类似：

class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length + 1][nums2.length + 1];for(int i = 1;i <= nums1.length;i++) {for(int j = 1;j <= nums2.length;j++) {if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);}}return dp[nums1.length][nums2.length];}
}

最大子数组和

题目链接：53. 最大子数组和

解题逻辑：

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i]表示以i结尾的字符串的最大子序和
• 递推式：一个可以从dp[i - 1]这种情况（也就是不包含当前i的连续字符串的最大子序和）递推过来，也可以把当前字符当作子序头元素。哪个大选哪个：dp[i] = Math.max(dp[i - 1] + nums[i],nums[i])。
• 初始化：dp[0]初始化为nums[0]
• 遍历方向：从左往右遍历

解题代码：

class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int max = nums[0];for(int i = 1;i < nums.length;i++) {dp[i] = Math.max(dp[i - 1] + nums[i],nums[i]);if(max < dp[i]) max = dp[i];}return max;}}

判断子序列

题目链接：392. 判断子序列

解题逻辑：

这一题可以转化为最长公共子序列，只要最后求出的最长公共子序列的长度为s的长度，那么就说明s为t的子序列。

解题代码：

class Solution {public boolean isSubsequence(String s, String t) {int[][] dp = new int[s.length() + 1][t.length() + 1];int max = 0;for(int i = 1;i <= s.length();i++) {for(int j = 1;j <= t.length();j++) {if(s.charAt(i - 1) == t.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);}}}return dp[s.length()][t.length()] == s.length();}
}

不同的子序列

题目链接：115. 不同的子序列

解题思路：

要统计s的子序列中t出现的次数，其实可以将这个问题转化为要将s转化为t，有多少删除元素的方式。

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示s[0,i -1]子序列中出现t[0,j-1]的个数为dp[i][j]
• 递推式：当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]。dp[i - 1][j]表示不算新添加的s[j - 1]s中t出现的次数，dp[i - 1][j - 1]表示算新添加的s[j - 1]s中t出现的次数。
• 初始化：dp[0]初始化为nums[0]
• 遍历方向：从左往右遍历

代码如下：

class Solution {public int numDistinct(String s, String t) {int[][] dp = new int[s.length() + 1][t.length() + 1];for(int i = 0;i <= s.length();i++) dp[i][0] = 1;for(int i = 1;i <= t.length();i++) dp[0][i] = 0;for(int i = 1;i <= s.length();i++) {for(int j = 1;j <= t.length();j++) {if(s.charAt(i - 1) == t.charAt(j - 1)) dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];else dp[i][j] = dp[i - 1][j];}}return dp[s.length()][t.length()];}
}

两个字符串的删除操作

题目链接：583. 两个字符串的删除操作

解题思路：

该问题可以直接转化为求最长公共子序列，然后根据最长公共子序列的长度可以计算出删除的最小步数

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示word1[0,i -1]字符串和word2[0,j-1]字符串所形成的最长公共子序列。
• 递推式：
  • word1[i - 1] == word2[j - 1],dp[i][j] = dp[i - 1][j - 1] + 1;
  • 不相等,dp[i][j] = max(dp[i - 1][j],dp[i][j - 1])
• 初始化：全初始化为0
• 遍历方向：从左往右遍历，从上往下

class Solution {public int minDistance(String word1, String word2) {int[][] dp = new int[word1.length() + 1][word2.length() + 1];for(int i = 1;i <= word1.length();i++) {for(int j = 1;j <= word2.length();j++) {if(word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);}}}int max = dp[word1.length()][word2.length()];return word1.length() + word2.length() - 2 * max;}
}

编辑距离

题目链接：72. 编辑距离

解题逻辑：

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示以i - 1结尾的word1转换成以j - 1结尾的word2的最小操作数
• 递推式：
  • word1[i - 1] == word2[j - 1]，说明不需要操作，dp[i][j] = dp[i - 1][j - 1];
  • 不相等，那么就会涉及到三种操作增、删、改，其中增删是一种相对操作，对word1的增，也可以通过对word2的删来实现，所以增、删考虑为一种情况。也就是说此时涉及到两种情况
    • 如果是使用增删操作，那么操作数为dp[i - 1][j] + 1、dp[i][j - 1] + 1
    • 如果是使用改操作，那么操作数为dp[i - 1][j - 1] + 1
    • 三个表达式中取最小的
• 初始化：dp[i][0]表示i - 1结尾的word1转换成空串的步骤，所以初始化为i；dp[0][j]与上面同理。
• 遍历方向：从左往右遍历，从上往下

class Solution {public int minDistance(String word1, String word2) {int[][] dp = new int[word1.length() + 1][word2.length() + 1];//初始化for(int i = 0;i <= word1.length();i++) dp[i][0] = i;for(int j = 0;j <= word2.length();j++) dp[0][j] = j;for(int i = 1;i <= word1.length();i++) {for(int j = 1;j <= word2.length();j++) {if(word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];else dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1,dp[i][j - 1] + 1),dp[i - 1][j - 1] + 1);}}return dp[word1.length()][word2.length()];}
}

回文子串

题目链接：647. 回文子串

解题逻辑：

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示s[i,j]是否为回文子串
• 递推式：if(s[i] == s[j])
  • 情况1：i = j dp[i][j] = true;
  • 情况2：j = i + 1 dp[i][j] = true;
  • 情况3：j > i + 1 dp[i][j] = dp[i + 1][j - 1]
• 初始化：全部初始化为false
• 遍历方向：dp[i][j]依赖于左下角的值，所以从下往上，从左往右

解题代码：

class Solution {public int countSubstrings(String s) {int n = s.length();boolean[][] dp = new boolean[n][n];int result = 0;for(int i = n - 1;i >= 0;i--) {for(int j = i;j < n;j++) {if(s.charAt(i) == s.charAt(j)) {if(i == j) {result++;dp[i][j] = true;}else if(i + 1 == j) {result++;dp[i][j] = true;}else if(dp[i + 1][j - 1]){result++;dp[i][j] = true;}}}}return result;}
}

最长回文子序列

题目链接：516. 最长回文子序列

解题逻辑：

我们从dp四部曲来分析这个问题：

• dp数组含义：dp[i][j]表示s[i,j]最长的回文子序列
• 递推式：s[i] == s[j] dp[i][j] = dp[i + 1][j - 1] + 2。如果不相等，dp[i][j] = max(dp[i + 1][j],dp[i][j - 1])。
• 初始化：全部初始化为false
• 遍历方向：dp[i][j]依赖于左下角的值，所以从下往上，从左往右

解题代码：

class Solution {public int longestPalindromeSubseq(String s) {int n = s.length();int[][] dp = new int[n][n];for(int i = n - 1;i >= 0;i--) {for(int j = i;j < n;j++) {if(s.charAt(i) == s.charAt(j)) {if(i == j) {        dp[i][j] = 1;}else if(i + 1 == j) {       dp[i][j] = 2;}else{dp[i][j] = dp[i + 1][j - 1] + 2;}}else {dp[i][j] = Math.max(dp[i + 1][j],dp[i][j - 1]);}}}return dp[0][n - 1];}
}

最长回文子串

题目链接：5. 最长回文子串

解题逻辑：

直接在回文子串的基础上加一个结果收集比较逻辑即可

解题代码：

class Solution {public String longestPalindrome(String s) {int n = s.length();boolean[][] dp = new boolean[n][n];int start = 0;int maxLen = 1;for(int i = n - 1;i >= 0;i--) {for(int j = i;j < n;j++) {if(s.charAt(i) == s.charAt(j)) {if(i == j) {dp[i][j] = true;if(j - i + 1 >= maxLen) {start = i;maxLen = j - i + 1;}}else if(i + 1 == j) {dp[i][j] = true;if(j - i + 1 >= maxLen) {start = i;maxLen = j - i + 1;}}else if(dp[i + 1][j - 1]){dp[i][j] = true;if(j - i + 1 >= maxLen) {start = i;maxLen = j - i + 1;}}}}}return s.substring(start,start + maxLen);}
}