当前位置：首页 > news >正文

基础动态规划问题

news 2025/10/6 8:11:22

线性DP

背包问题

01背包问题定义状态表示f[i][j], 表示考虑前i个物品, 总体积不超过j, 的选择方案中价值最大的方案的价值, 对于f[i][j]方案可以由当前物品的选择情况进行划分, 如果不选择当前物品f[i - 1][j], 如果选择当前物品价值就是f[i - 1][j - v[i]] + w[i], 因为当前状态是由f[i - 1]层数给出, 因此数组可以省下一个维度, 使用f[j]代替状态表示, 但是第二层体积需要进行倒序枚举, 因为对于当前状态f[i][j]需要的状态是f[i - 1][x] x < j
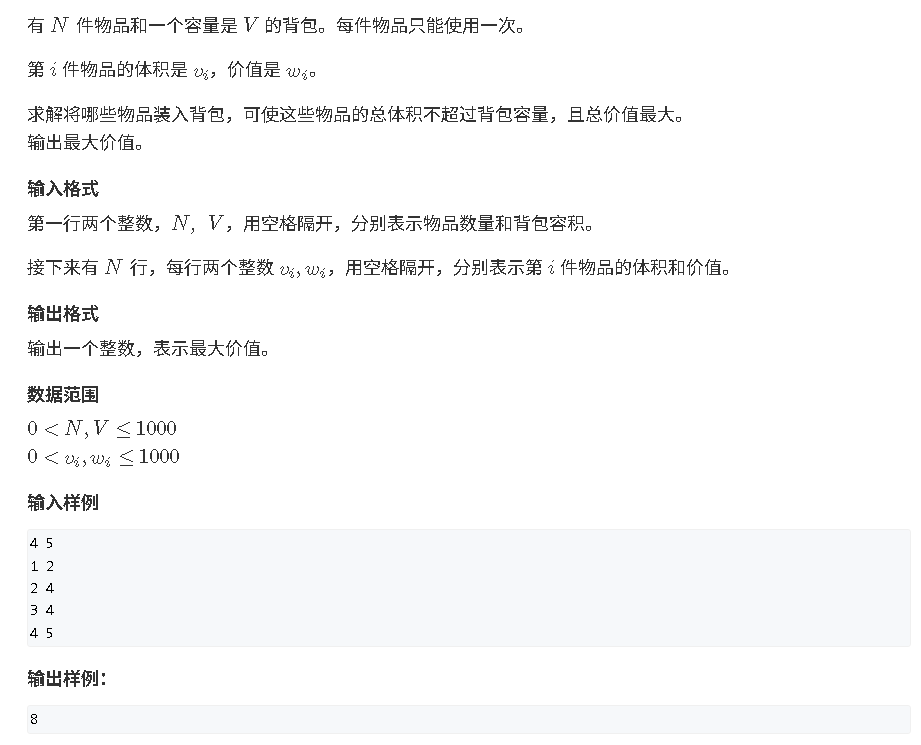
在这里插入图片描述

#include <bits/stdc++.h>using namespace std;const int N = 1010, M = 1010;int n, m;
int w[N], v[N];
int f[M];int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = m; j >= v[i]; --j) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << '\n';return 0;
}

完全背包问题
状态表示不需要发生改变, 因为物品数量是无限的, 状态转移方式需要改变, 对于当前物品可选择的次数上限是 $mv[i]\frac{m}{v[i]}$

状态计算
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i], f[i - 1][j - 2 * v[i]] + 2 * w[i] , ... , f[i - 1][j - k * v[i]] + k * w[i])
再观察f[i][j - v[i]]的计算过程
f[i][j - v[i]] = max(f[i - 1][j - v[i]], f[i - 1][j - 2 * v[i]] + w[i], f[i - 1][j - k * v[i]] + (k - 1) * w[i])

状态转移方程转化为f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]), 对比01背包问题的状态转移方程, 因为当前层状态只与上一层状态有关, 因此也可以优化掉一维, 但是因为当前状态f[i][j], 需要的上一层状态是f[i - 1][j]并且需要当前i层数的f[i][j - v[i]]状态, 只能正序枚举体积j, 状态转移方程优化为f[j] = max(f[j], f[j - v[i]] + w[i])
在这里插入图片描述

#include <bits/stdc++.h>using namespace std;const int N = 1010, M = 1010;int n, m;
int w[N], v[N];
int f[M];int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = v[i]; j <= m; ++j) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << '\n';return 0;
}

在这里插入图片描述
多重背包问题朴素算法 $\times m \times c)$

#include <bits/stdc++.h>using namespace std;const int N = 110, M = 110;int n, m;
int v[N], w[N], c[N];
int f[N][M];int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> c[i];for (int i = 1; i <= n; ++i) {for (int j = 0; j <= m; ++j) {f[i][j] = f[i - 1][j];for (int k = 0; k <= min(c[i], j / v[i]); ++k) {f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}}cout << f[n][m] << '\n';return 0;
}

多重背包问题二进制优化 $\times m \times log{C})$

#include <bits/stdc++.h>using namespace std;const int N = 1010, M = 2010;int n, m;
int v[N], w[N], c[N];
int new_v[N * 12], new_w[N * 12];
int f[M];int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> c[i];int cnt = 1;for (int i = 1; i <= n; ++i) {int val = 1;while (val <= c[i]) {new_v[cnt] = val * v[i];new_w[cnt++] = val * w[i];c[i] -= val;val <<= 1;}if (c[i]) {new_v[cnt] = c[i] * v[i];new_w[cnt++] = c[i] * w[i];}}for (int i = 1; i <= cnt; ++i) {for (int j = m; j >= new_v[i]; --j) {f[j] = max(f[j], f[j - new_v[i]] + new_w[i]);}}cout << f[m] << '\n';return 0;
}

多重背包问题单调队列优化 $\times m)$

#include <bits/stdc++.h>using namespace std;const int N = 1010, M = 20010;int n, m;
int v[N], w[N], c[N];
int f[M], tmp[M];int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> c[i];int q[M];for (int i = 1; i <= n; ++i) {memcpy(tmp, f, sizeof f);for (int r = 0; r < v[i]; ++r) {int h = 0, t = -1;for (int j = r; j <= m; j += v[i]) {while (h <= t && j - q[h] > c[i] * v[i]) h++;while (h <= t && tmp[j] >= tmp[q[t]] + (j - q[t]) / v[i] * w[i]) t--;q[++t] = j;f[j] = tmp[q[h]] + (j - q[h]) / v[i] * w[i];}}}cout << f[m] << '\n';return 0;
}