红黑树动画演示
红黑树简介
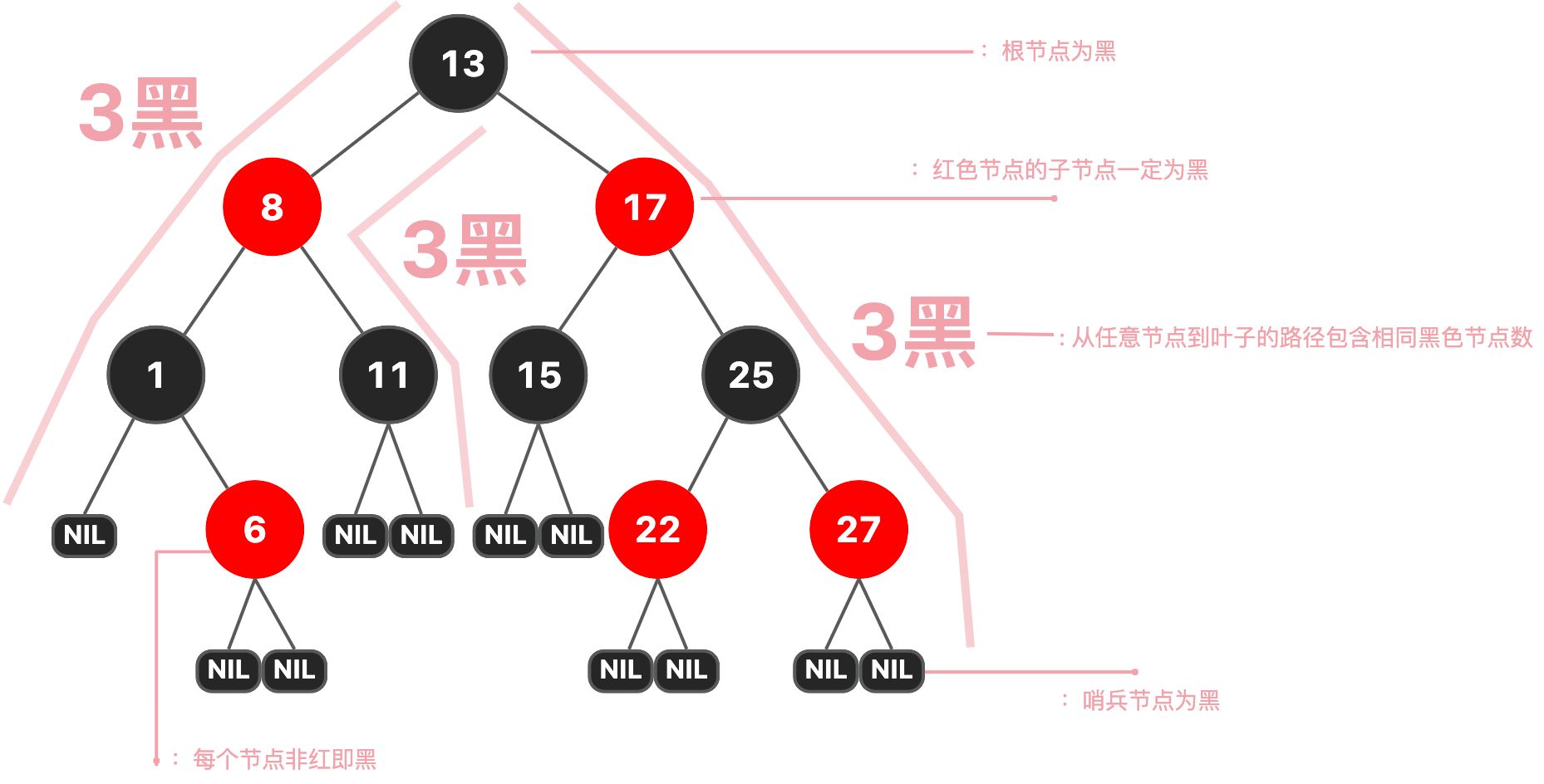
- 每个节点非红即黑;
- 根节点为黑;
- 叶子节点(NIL哨兵)为黑;
- 红色节点的子节点必为黑(即无连续红节点);
- 从任意节点到叶子的路径包含相同黑节点数(定义黑高bh)
- 任一节点左右子树的高度相差不超过两倍
左根右, 根叶黑, 不红红,黑路同。
红黑树也是一种二叉搜索树,也是为了尽量平衡二叉搜索树的,只不过策略采用的和AVL不一样。 AVL是计算层高,但是这个要有5个条件都满足才行。
为什么要五个条件这么复杂呢? 原因是这样的规则,会将树的平衡程度放低,没有AVL树那么严格的平衡,随之而来的便是,我们也没有那么勤快的整理整棵树。因为律法宽松,所以抓的人少,你可以简单的这么认为。
红黑树的排布
首先我们要记住上面提到的四大原则,这个原则是插入时条件判断的原则。并不是整个红黑树的原则。这是两个场景。总之根据这四个原则,能够构建出符合红黑树原则的树!
左根右, 根叶黑, 不红红,黑路同。
- 左根右,代表 左 > 根 > 右。 实际上是BST的规则
- 根叶黑: 根节点和叶子节点,是黑色的!如果没有叶子节点,那我们的空哨节点也是黑色的。
- 不红红: 代表插入元素的时候不允许出现两个红色节点连接到一起。这个动画中观察即可!
- 黑路同: 代表根节点到各大叶子节点经历的黑色节点是一样的数量。
这个有点子复杂, 对比平衡树,规则要多得多。因为判断失衡的条件是,不满足以上5条规则。随便一个都能触发。
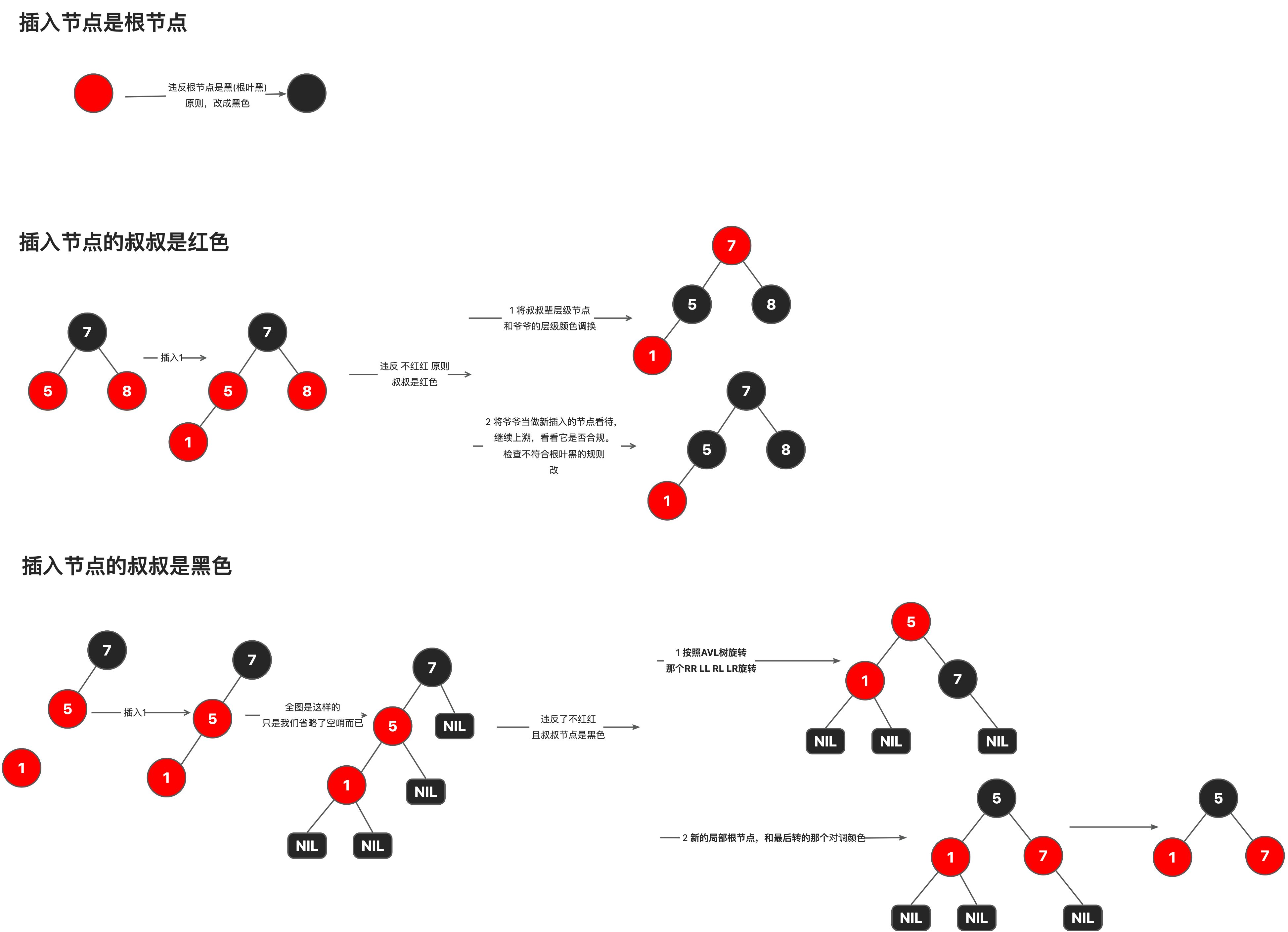
调整的时候,要看爷爷,看叔叔,还看叔叔的颜色。颜色不一样调整方式不一样。
- 首先我们落入一个节点的时候,按照二叉搜索树的方式落!该在哪里就是在哪里。
- 落的新点,全都按做是红色节点,注意这时候判断失衡已经不是计算层高了,而是看是不是两个红色的相连。两个红色相连就得调整!因为已经不符合“红色节点的子节点一定为黑”这个规则了。
- 调整,这环节分三路
- 插入节点是根节点
- 插入节点的叔叔是红色的
- 插入节点的叔叔是黑色的
这三路用图表示下哈:
红黑树构建过程

红黑树 VS AVL
- AVL因为更加均衡,在查询的时候效率更高
- 红黑树因为排布的次数少,在添加删除方面效率更高。
