逻辑门可以实现数学运算，逻辑思维与数学思维谁更基本

1. 介绍

        逻辑思维和数学运算思维并非彼此衍生的关系，而是像同一棵大树上的两根强大分支。它们的共同基础，可以追溯到人类心智中几种更根本、更原始的能力。

下图清晰地展示了这些基础能力如何共同支撑起逻辑与数学思维：

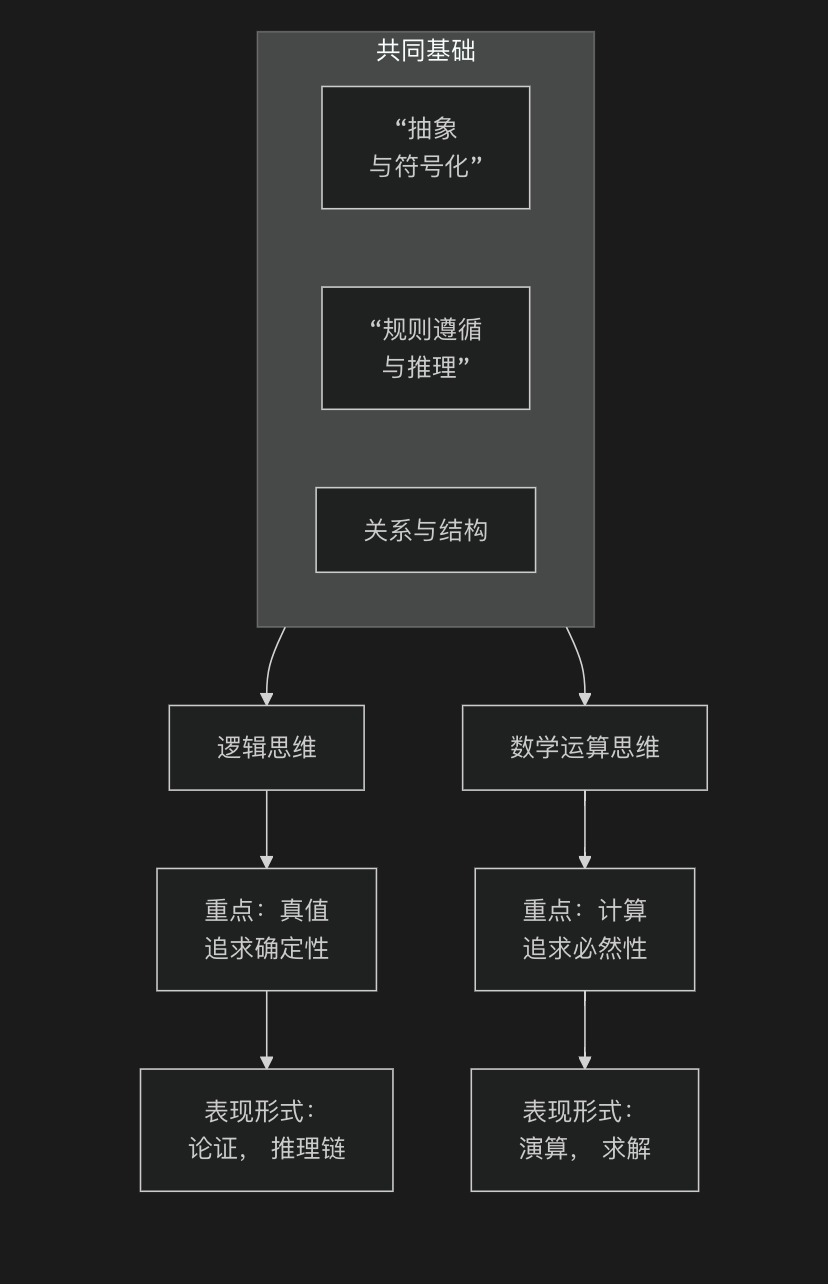
2. 对共同基础的详细阐释

2.1. 抽象与符号化

这是最底层的基石。两种思维都要求大脑能够忽略具体事物的丰富细节，只提取某些特定属性或关系，并用符号（语言、数字、变量、逻辑连接词）来代表它们。

在逻辑中

        我们忽略“苏格拉底”这个人的所有其他特性（他是雅典人、哲学家），只将其抽象为一个符号 S；忽略“会死”的所有复杂生物学含义，只抽象为属性 M。然后我们只关心 S 和 M 之间的关系。

在数学中

        我们忽略三只羊、三棵树、三座山的具体差异，只抽象出“3”这个数量概念。我们用符号 + 来代表一种特定的关系，而不管相加的是苹果还是距离。

没有抽象，思维将永远被禁锢在具体个例中，无法形成普遍性的思考。

2.2. 规则遵循与推理

        两种思维都不是随意的，它们都依赖于严格应用一套预先定义的规则系统，从已知信息推导出新信息。

在逻辑中

        规则是推理规则（如Modus Ponens：如果P则Q，现在有P，所以有Q）。我们从前提开始，通过一步步应用规则，得到结论。

在数学中

        规则是公理、定义和运算法则（如加法交换律、分数运算法则）。我们从已知条件或公理开始，通过一步步演算或证明，得到结果。

这种对规则的严格遵循，保证了思维过程的一致性和有效性。

2.3. 关系与结构

两种思维都极度关注元素之间的关系，而非元素本身。它们都是在操作一个由关系构成的结构。

在逻辑中

        我们关心的是命题之间的真值关系（“如果...那么...”、“...且...”、“...或...”）。

在数学中

        我们关心的是数字或变量之间的函数关系、运算关系、空间关系（“大于”、“等于”、“函数映射”）。

正是对这种抽象关系的敏感和操作能力，使得逻辑和数学能够描述世界的普遍规律。

 

3. 思维倾向的细微差异

尽管根植于共同的基础，但两者的侧重点有所不同，这导致了它们不同的“风味”和应用场景：

逻辑思维的核心是“真值”

        它追求的是论证的有效性和命题的真假。它问的是：“从这些前提中，必然能得出什么结论？” 其核心是确定性。

数学运算思维的核心是“计算”

        它追求的是从初始量通过变换得到结果量。它问的是：“如果这样操作，会得到什么结果？” 其核心是必然性（由规则保证的必然结果）。

        可以说，逻辑更侧重于“推断”，而数学运算更侧重于“变换”。但深究下去，推断也是一种变换（真值的变换），变换也需要逻辑来保证其正确性。它们在最深的层次上是相通的，共同构成了人类理性的两大支柱。

        因此，它们的共同根源，就是人类心智的抽象能力、规则系统和关系认知。这正是理性之所以可能的基础。

4. 两者可以互相表达

        逻辑与数学可以互相表达（即互相翻译、互相嵌入），这不仅仅是技术上的巧合，而是深刻地揭示了理性世界的统一性。这意味着以下几点。

 

4.1. 它们共享同一个深层结构

        两者可以互相表达，强烈暗示了在表面不同的符号和应用之下，逻辑思维和数学运算思维共享着同一个抽象的、形式化的核心结构。

逻辑可以表达数学

        这体现在数学的基础可以建立在逻辑之上（如罗素和怀特海德的《数学原理》试图做的）。集合论可以作为数学的基础，而集合论本身又可以公理化，其公理可以用纯逻辑语言（一阶逻辑与等词）来陈述。加、乘、指数等数学运算，最终都可以定义为纯逻辑的概念。

数学可以表达逻辑

        这体现在逻辑的语义和模型可以用数学结构来研究（模型论、布尔代数）。一个逻辑系统是否一致、是否完备，可以转化为关于数学形式系统的问题。乔治·布尔的工作就是用代数来研究逻辑规律。

        这就像水和冰，形态不同，但本质都是H₂O。逻辑和数学是同一套理性规则系统的两种不同显现方式。

 

4.2. 理性思维可能本质上是“形式系统的操作”

        如果逻辑和数学可以互通，那么人类引以为豪的理性思维，其内核可能并非依赖于某种神秘的“理性之光”，而是基于一种对形式符号系统进行操作的能力。

这种能力包括：

        语法识别：识别符号的合法组合。

        规则应用：根据明确的规则生成新的符号序列。

        模式匹配：识别符号序列中的重复结构。

        我们的理性思考，无论是推导一个逻辑结论还是解一个方程，可能都是在心智中（无意识地）实例化了这样一个形式系统并对其进行操作。我们感受到的“理解”和“洞察”，可能是大脑对这个过程的一种主观体验。

 

4.3. 计算主义的有力证据

这一事实是计算主义（认为心智本质上是计算过程）的强有力支持。

图灵机与丘奇-图灵论题

        图灵机是一个极简的逻辑-数学模型，但它被证明可以计算任何“能行可计算”的函数。这意味着，任何可以用逻辑或数学精确描述的过程，原则上都可以被图灵机（即计算机）执行。

        如果理性思维可以还原为逻辑/数学操作，而逻辑/数学操作又可以由图灵机实现，那么一个必然的推论就是：原则上，计算机可以模拟人类的理性思维。

        这为人工智能奠定了理论基础。我们今天所有的AI，从根本上都在利用这种逻辑与数学的互通性。

 

4.4. 它指向了“理性”的边界和局限性

既然逻辑和数学可以互相表达，那么它们也必然共享同样的局限性。

哥德尔不完备定理

        这个打击了数学基础研究的定理，同样适用于足够强大的逻辑系统。它表明，任何一个足够强大、能表达基本算术的形式系统（无论是披着逻辑的外衣还是数学的外衣），都必然是不完全的（存在无法证明的真命题）且无法证明自身的一致性。

        这意味着什么？ 这意味着人类的理性工具（逻辑和数学）本身存在内在的、不可逾越的极限。我们无法用一个系统来完全“捕获”所有的数学真理，也无法用这个系统本身来最终证明它不会产生矛盾。

        因此，可互相表达的逻辑与数学，共同为我们理性的能力划定了边界。 绝对的、无矛盾的、完备的理性体系是一个无法实现的梦想。

 

4.5. 总结

        两者可以互相表达，这意味着：

        统一性

                逻辑与数学是同一枚硬币的两面，共同构成了一个统一的、自洽的理性框架。

        本质性

                理性思维可能根植于对形式符号系统的操作，而非具体内容。a

        可计算性

                为人工智能提供了可能性，因为计算机是处理形式系统的完美工具。

        局限性

                同时，它也清晰地展示了理性本身固有的、根本性的限制。

        最终，这引导我们走向一个既令人谦卑又令人兴奋的结论：我们赖以理解世界的理性工具，既无比强大，又天生带有无法自愈的“裂纹”。正是这种统一性与局限性并存的特质，定义了人类理性的真实图景。