当前位置：首页 > news >正文

强化学习入门(1)：概念、Sarsa、Q-Learning、Dyna-Q

news 2025/10/4 14:25:52

什么是强化学习

强化学习是一种让智能体在未知环境中通过试错自我进化的人工智能范式，核心在于把学习过程建模为“状态-动作-奖励”的闭环：智能体观察当前状态，根据策略选择一个动作，环境立即返回一个标量奖励并转移到下一个状态，目标是最大化长期回报（通常是折扣累积奖励）。为了平衡探索与利用，算法需要一边尝试看似次优的动作以发现潜在高回报，一边利用已学到的信息避免无谓损失。

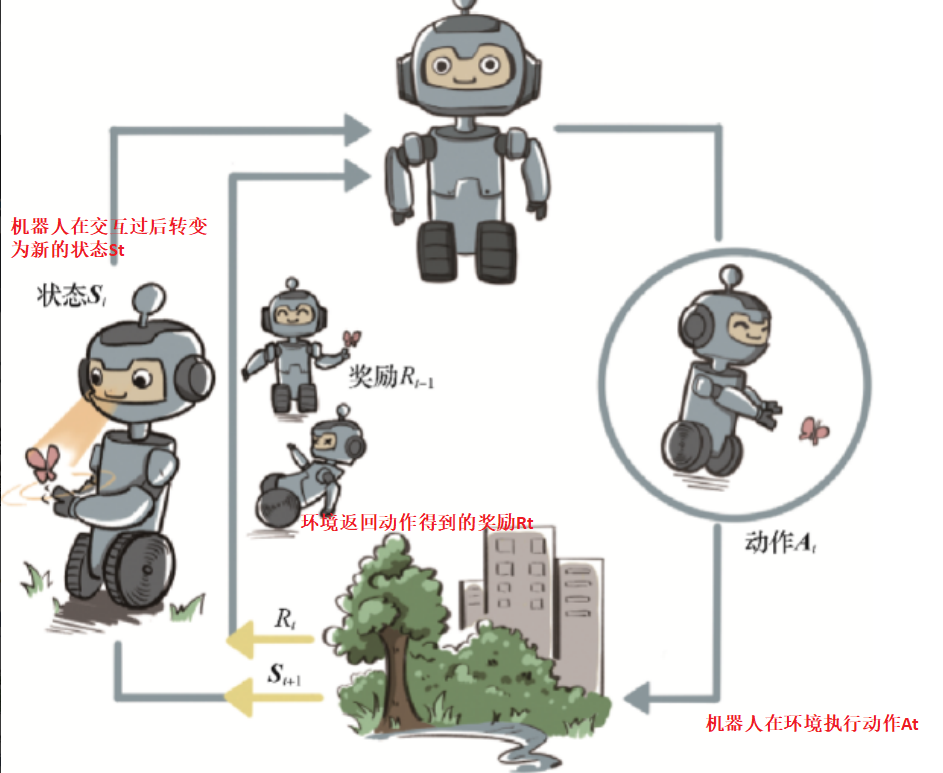
与监督学习依赖人工标注的 “正确答案” 不同，强化学习不需要预先提供样本标签，而是让智能体在与环境的动态交互中探索有效路径，同时也会利用已有的经验（ exploitation ）避免重复无效尝试，平衡 “探索” 与 “利用” 是其关键挑战之一。比如训练机械臂抓取物体时，机械臂每一次成功抓取会获得正向奖励，抓取失败则无奖励或获得负奖励，通过反复尝试，它会逐渐学习到最适合的发力角度、力度等动作组合，最终形成稳定的抓取策略。

这两个公式分别对应监督学习中最优模型的求解和强化学习中最优策略的求解，核心是从“损失最小化”和“奖励最大化”两个角度，定义如何找到最理想的学习目标（模型或策略）。

监督学习核心逻辑：找一个模型，让 “预测值与真实标签的差距（损失）” 尽可能小。

模型argmin：“在所有可能的模型中，找到使后面表达式最小的那个模型”。
E(特征,标签)∼数据分布：对 “特征 - 标签” 服从的真实数据分布求期望（可以理解为 “对所有可能的样本取平均”）。
损失函数(标签,模型(特征))：衡量 “模型用特征预测的结果” 和 “真实标签” 差距的函数（比如分类任务常用交叉熵，回归任务常用均方误差）。

强化学习核心逻辑：找一个策略，让 “智能体在状态下执行动作后获得的奖励” 尽可能大

argmax：“在所有可能的策略中，找到使后面表达式最大的那个策略”。
E(状态,动作)∼策略的占用度量：对 “状态 - 动作” 服从的 “策略占用度量” 求期望（可以理解为 “对智能体在策略下所有可能的‘状态 - 动作’组合取平均”）。“策略的占用度量” 描述了策略在长期交互中，对 “状态 - 动作” 的选择频率。
奖励函数(状态,动作)：衡量 “智能体在某状态下执行某动作” 能获得的即时奖励（比如游戏里吃到金币得正奖励，碰到敌人得负奖励）。

马尔科夫

马尔科夫：系统的下一刻状态只依赖当前状态和刚刚采取的动作，而与更早之前发生过什么彻底无关。换句话说，历史被“压缩”成当前状态，一旦把 s_t 握在手里，就可以把前面所有轨迹忘掉。公式定义为： $P(S_{t+1}|S_t) = P(S_{t+1}|S_1, \ldots, S_t)$

在强化学习中，这一特性进一步延伸为 马尔科夫决策过程（MDP），它在马尔科夫过程的基础上加入了 “动作” 和 “奖励”：智能体在当前状态下选择动作，环境会根据当前状态和动作转移到下一个状态，并给出奖励。这里的状态转移依然满足马尔科夫性 —— 下一个状态的概率仅由当前状态和当前动作决定，与之前的状态、动作序列无关，这是构建强化学习环境模型的核心假设。

马尔可夫链（Markov Chain）

马尔可夫链（Markov Chain）：马尔可夫链是一种具有马尔可夫性质的随机过程，其由状态空间S和状态转移矩阵P组成。

状态转移矩阵：
$\mathcal{P} = \begin{bmatrix} P(s_1|s_1) & \cdots & P(s_n|s_1) \\ \vdots & \ddots & \vdots \\ P(s_1|s_n) & \cdots & P(s_n|s_n) \end{bmatrix}$

需注意：状态转移矩阵的每一行的和均为1

状态空间矩阵： $\mathcal{S} = \{s_1, s_2, \ldots, s_n\}$

对于如下状态图：

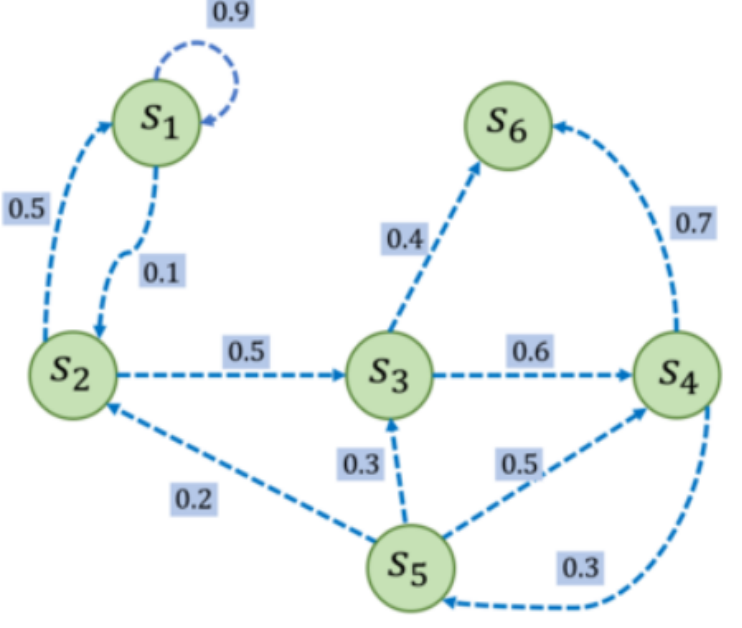
其状态转移矩阵P为 $\mathcal{P} = \begin{bmatrix} 0.9 & 0.1 & 0 & 0 & 0 & 0 & 0 \\ 0.5 & 0 & 0.5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.6 & 0 & 0.4 \\ 0 & 0 & 0 & 0 & 0.3 & 0.7 \\ 0 & 0.2 & 0.3 & 0.5 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}$

import numpy as np
np.random.seed(0)
# 定义状态转移概率矩阵P
P = [[0.9, 0.1, 0.0, 0.0, 0.0, 0.0],[0.5, 0.0, 0.5, 0.0, 0.0, 0.0],[0.0, 0.0, 0.0, 0.6, 0.0, 0.4],[0.0, 0.0, 0.0, 0.0, 0.3, 0.7],[0.0, 0.2, 0.3, 0.5, 0.0, 0.0],[0.0, 0.0, 0.0, 0.0, 0.0, 1.0],
]
P = np.array(P)rewards = [-1, -2, -2, 10, 1, 0]  # 定义奖励函数
gamma = 0.5  # 定义折扣因子# 给定一条序列,计算从某个索引（起始状态）开始到序列最后（终止状态）得到的回报
def compute_return(start_index, chain, gamma):G = 0for i in reversed(range(start_index, len(chain))):G = gamma * G + rewards[chain[i] - 1]    # 折扣累积奖励return G# 一个状态序列,s1-s2-s3-s6
chain = [1, 2, 3, 6]
start_index = 0
G = compute_return(start_index, chain, gamma)
print("根据本序列计算得到回报为：%s。" % G)

折扣累积奖励

假设智能体处于一个状态序列中，在每一个时间步都会获得一个即时奖励。这段代码通过不断迭代更新 G，来计算从当前时刻开始，后续所有奖励经过折扣后的总和。

G = gamma * G + rewards[chain[i] - 1]

具体计算逻辑是，每次更新时，先将当前的折扣累积奖励 G 乘以折扣因子 gamma，这相当于把之前计算的折扣累积奖励按照折扣因子进行 “贬值”，然后加上当前时间步获得的即时奖励 rewards[chain[i] - 1]。这样做的目的是为了根据新的信息（即时奖励）更新对未来回报的估计。

在时序差分学习中，这种更新是通过逐步逼近的方式来进行的，即通过不断地根据新的经验来调整对预期回报的估计。这种方法比基于模型的方法（如动态规划）更高效，因为它不需要环境的完整模型，只需要通过与环境的交互来学习。

价值函数

状态价值函数

状态价值函数 V(s) 表示在状态 s 下，从该状态开始并遵循某个策略所能获得的期望回报。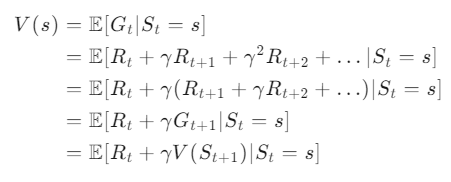

$V(s) = r(s) + \gamma \sum_{s' \in S} p(s'|s) V(s')$

其中：

V(s)：状态 s 的价值，表示从状态 s 出发，按照当前策略与环境交互，能获得的长期累积奖励的期望。
Gt：累积奖励（Return），即从时刻 t 开始的所有未来奖励的加权和：Gt=Rt+γRt+1+γ2Rt+2+…（γ 是折扣因子，0≤γ≤1，用于削弱远期奖励的权重）。
E[⋅∣St=s]：“在当前状态为 s 的条件下，对后面的随机变量取期望”（因为环境和策略都有随机性，所以用期望描述平均收益）。

下面是公式推导：

代码如下：

def compute(P, rewards, gamma, states_num):''' 利用贝尔曼方程的矩阵形式计算解析解,states_num是MRP的状态数 '''rewards = np.array(rewards).reshape((-1, 1))  #将rewards写成列向量形式value = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P),rewards)return valueV = compute(P, rewards, gamma, 6)
print("MRP中每个状态价值分别为\n", V)

策略和动作价值函数

策略函数：在状态 s 下采取动作 a 的概率。定义为 $\pi(a|s) = P(A_t = a | S_t = s)$

动作价值函数：动作价值函数（或称为Q函数）描述了在状态 s 采取动作 a 后所获得的期望回报。 $Q^{\pi}(s, a) = \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a]$ ，即 $Q^{\pi}(s, a) = r(s, a) + \gamma \sum_{s' \in S} P(s' | s, a) V^{\pi}(s')$

由于策略 π 决定了在每个状态下采取的动作，我们可以将期望回报进一步展开，得到完整的状态价值函数 $V^{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s]$ ，得到 $V^{\pi}(s) = \sum_{a \in A} \pi(a|s) Q^{\pi}(s, a)$ 。

将上面式子完整展开可得其贝尔曼方程为：

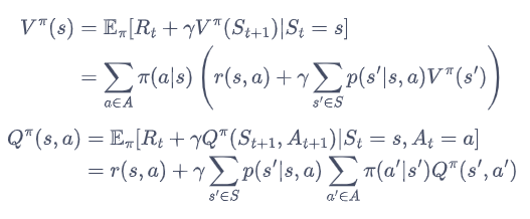
无模型的强化学习

无模型的强化学习算法不需要事先知道环境的奖励函数和状态转移函数，而是直接使用和环境交互的过程中采样到的数据来学习，这使得它可以被应用到一些简单的实际场景中。

经典的强化学习算法有：Sarsa算法、Q-Learning算法

蒙特卡洛方法

蒙特卡洛方法（Monte-Carlo methods）也被称为统计模拟方法，是一种基于概率统计的数值计算方法。运用蒙特卡洛方法时，我们通常使用重复随机抽样，然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。

一个简单的例子是用蒙特卡洛方法来计算圆的面积。例如，在图 3-5 所示的正方形内部随机产生若干个点，细数落在圆中点的个数，圆的面积与正方形面积之比就等于圆中点的个数与正方形中点的个数之比。如果我们随机产生的点的个数越多，计算得到圆的面积就越接近于真实的圆的面积。

一个状态的价值是它的期望回报，那么一个很直观的想法就是用策略在环境中采样很多条序列，计算从这个状态出发的回报再求其期望就可以了，公式如下： $V^{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s] \approx \frac{1}{N} \sum_{i=1}^{N} G_t^{(i)}$

策略迭代算法

策略迭代（Policy Iteration）是强化学习中的一种经典算法，用于找到给定马尔可夫决策过程（MDP）的最优策略。该算法通过迭代地执行两个步骤来实现：策略评估（Policy Evaluation）和策略改进（Policy Improvement）。

策略评估（Policy Evaluation）：初始化价值函数 $V_0(s)$ ，可以是零或任意值。对于当前策略 $\pi$ ，计算每个状态 s 的价值函数 $V^{\pi}(s)$ 。

策略改进（Policy Improvement）：使用贝尔曼方程，通过迭代方法求解，直到价值函数收敛。

对于每个状态 s，计算在该状态下采取每个可能动作 a 的动作价值函数 $Q^{\pi}(s, a)$ ： $Q^{\pi}(s, a) = r(s, a) + \gamma \sum_{s' \in S} p(s'|s, a) V^{\pi}(s')$ ，选择使 $Q^{\pi}(s, a)$ 最大化的动作 $a^*$ 作为新策略 $\pi'(s)$ ： $\pi'(s) = \arg\max_{a \in A} Q^{\pi}(s, a)$
然后求解新的价值函数： $V^{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s] = \sum_{a \in A} \pi(a|s) \left( r(s, a) + \gamma \sum_{s' \in S} p(s'|s, a) V^{\pi}(s') \right)$

如果新策略 $\pi'$ 与旧策略 $\pi$ 不同，则令 $\pi = \pi'$ 并返回步骤 2。否则，算法终止，当前策略即为最优策略。

通过策略迭代，智能体可以学习到在不同状态下采取的最佳动作，从而最大化其长期回报。这种方法在理论上是强大的，但在高维或连续状态空间中计算复杂度较高，因此实践中常使用其他方法如值迭代或Q学习。

策略提升定理

策略提升定理（Policy Improvement Theorem）是强化学习中的一个基本概念，它说明了在马尔可夫决策过程（MDP）中，如果一个策略比另一个策略在至少一个状态下能获得更高的期望回报，那么这个策略就是更好的策略。

用数学公式表示就是：

如果 $\pi'(s) = \arg\max_{a \in A} Q^{\pi}(s, a)$ ，那么对于所有的状态 s，我们有 $V^{\pi'}(s) \geq V^{\pi}(s)$ ，并且在至少一个状态 s 下， $V^{\pi'}(s) > V^{\pi}(s)$ 。

具体来说，策略提升定理指出：给定一个策略 $\pi$ ，我们可以计算出在该策略下每个状态的期望回报，即状态价值函数 $V^{\pi}(s)$ 。然后，对于每个状态 s，我们可以计算出在该状态下采取每个可能动作 a 的期望回报，即动作价值函数 $Q^{\pi}(s, a)$ 。如果我们根据这些动作价值函数来选择动作，即选择使得 $Q^{\pi}(s, a)$ 最大化的动作 $a^*$ ，那么我们可以得到一个新的策略 $\pi'$ 。

策略提升定理告诉我们，新策略 $\pi'$ 至少和原策略 $\pi$ 一样好，并且在至少一个状态下比原策略好。这是因为新策略在每个状态下都选择了能够获得更高期望回报的动作。

这个定理是策略迭代算法的基础，它保证了通过策略评估和策略改进的交替进行，我们可以逐步找到最优策略。每次策略改进都不会降低策略的价值函数，因此这个过程是收敛的。

时序差分（TD）

蒙特卡洛方法和时序差分（TD）学习的更新方式在强化学习中用于估计价值函数，它们的主要区别体现在更新的时机、使用的数据以及更新的公式上。

蒙特卡洛方法的更新方式

蒙特卡洛方法通常用于离策略评估，其更新方式基于完整的采样轨迹。具体步骤如下：

采样轨迹：让智能体在环境中运行，直到达到终止状态，收集一系列状态、动作、奖励和下一个状态的序列，形成一个完整的轨迹。
计算回报：对于轨迹中的每个状态，计算从该状态开始到终止状态的累积折扣回报 $G_t$ 。
更新价值函数：使用这些回报来更新状态的价值函数。对于每个状态 s，更新规则可以表示为： $V(s) \leftarrow V(s) + \alpha \left( G_t - V(s) \right)$ 。其中， $\alpha$ 是学习率， $G_t$ 是从状态 s 开始的回报。

蒙特卡洛方法的更新是在轨迹结束后进行的，因此它是一种批量更新方法。

时序差分（TD）学习的更新方式

时序差分学习是一种在线学习方法，它在每个时间步或部分轨迹上进行更新。TD学习的核心是利用TD误差来更新价值函数，TD误差是实际奖励与价值函数估计之间的差异。具体步骤如下：

选择动作：根据当前策略选择一个动作。
观察结果：执行动作后，观察即时奖励 R 和下一个状态 S' 。
计算TD误差：计算TD误差 $\delta$ ，它是实际奖励与价值函数估计之间的差异： $\delta = R + \gamma V(S') - V(S)$ 。其中， $\gamma$ 是折扣因子。
更新价值函数：使用TD误差来更新当前状态的价值函数： $V(S) \leftarrow V(S) + \alpha \delta$ 。其中， $\alpha$ 是学习率。

时序差分学习可以是同策略的（on-policy），也可以是离策略的（off-policy），并且可以在每个时间步进行更新，这使得它比蒙特卡洛方法更数据高效。

这个公式描述了在给定策略 $\pi$ 下，状态 $s$ 的价值函数 $V^{\pi}(s)$ 的计算过程。状态价值函数表示从状态 s 开始，遵循策略 $\pi$ 所能获得的期望回报。

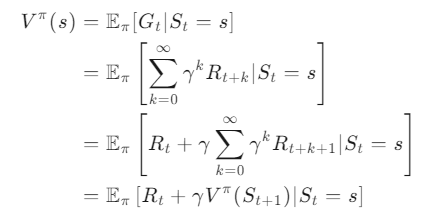
公式的推导过程如下：

定义状态价值函数： $V^{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s]$ 。这里， $G_t$ 是从时间步 t 开始的累积折扣回报，即从当前状态 s 开始，遵循策略 $\pi$ 进行一系列动作所获得的总奖励的折扣和。
展开回报： $V^{\pi}(s) = \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k} | S_t = s \right]$ 。这一步将累积折扣回报展开为无限序列，其中 $R_{t+k}$ 是在时间步 t+k 获得的奖励， $\gamma$ 是折扣因子，用于权衡未来奖励的重要性。
分解回报: $V^{\pi}(s) = \mathbb{E}_{\pi} \left[ R_t + \gamma \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} | S_t = s \right]$ 。这里，我们将即时奖励 $R_t$ 从序列中分离出来，并将剩余的回报序列向前移动一个时间步。
应用贝尔曼方程: $V^{\pi}(s) = \mathbb{E}_{\pi} \left[ R_t + \gamma V^{\pi}(S_{t+1}) | S_t = s \right]$ 。这一步利用了贝尔曼方程，将剩余的回报序列替换为从下一个状态 $S_{t+1}$ 开始的状态价值函数 $V^{\pi}(S_{t+1})$ 的期望值。这是因为在时间步 t+1 之后，我们仍然需要遵循策略 $\pi$ 来计算期望回报。

这个公式是策略评估和策略迭代算法的基础，它表明当前状态的价值函数可以通过即时奖励和下一个状态的价值函数来递归计算。通过这种方式，我们可以迭代地更新价值函数，直到它们收敛到真实值。

Sarsa算法

SARSA（State-Action-Reward-State-Action）算法是一种基于时序差分学习的强化学习算法，它属于策略迭代算法的一种。SARSA算法通过与环境的交互来学习一个策略，这个策略指导智能体在给定状态下选择动作。

Sarsa算法流程：

Sarsa用贪婪算法来选取在某个状态下动作价值最大的那个动作： $\arg\max_a Q(s, a)$
直接用时序差分算法来估计动作价值函数Q： $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha [r_t + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t)]$
形成循环：贪婪算法根据动作价值选取动作来和环境交互，再根据得到的数据用时序差分算法更新动作价值估计

然而贪婪算法可能会陷入局部最优解，而无法找到全局最优解。这是因为它在每一步都选择了当前看起来最好的选择，而没有考虑这些选择的组合可能不是最优的。另一方面，如果在策略提升中一直根据贪婪算法得到一个确定性策略，可能会导致某些状态动作对永远没有在序列中出现，以至于无法对其动作价值进行估计，进而无法保证策略提升后的策略比之前的好。

ε-贪婪（ε-greedy）

因此我们一般采用ε-贪婪（ε-greedy）策略：

它是一种在探索（exploration）和利用（exploitation）之间取得平衡的策略，常用于强化学习中。ε-贪婪策略在大多数情况下会采取当前估计的最佳动作，但以一定的概率 ε 随机选择一个动作，以此来探索环境。具体来说：

如果 $a = \arg\max_{a'} Q(s, a')$ ：这意味着动作 a 是在状态 s 下根据当前估计的 Q 值（动作价值函数）能够获得最大回报的动作。在这种情况下，采取该动作的概率是 $\epsilon / |\mathcal{A}| + 1 - \epsilon$ 。这里的 $1 - \epsilon$ 确保了即使在探索时，最优动作被选中的概率仍然较高。
其他动作：对于不是最优的动作，采取它们的概率是 $\epsilon / |\mathcal{A}|$ ，这是一个很小的概率，确保了探索的多样性。

Sarsa算法的伪代码

代码

首先我们设置一个一个悬崖行走环境类[CliffWalkingEnv]，用于强化学习训练。主要功能包括：

初始化：设置网格大小和智能体起始位置（左下角）。
执行动作：根据动作更新智能体位置，计算奖励和是否结束。
重置环境：将智能体位置恢复到初始状态。

坐标系原点在左上角，智能体目标是避开悬崖区域到达右下角终点。

import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm# 环境
class CliffWalkingEnv:def __init__(self, ncol, nrow):self.nrow = nrowself.ncol = ncolself.x = 0  # 记录当前智能体位置的横坐标self.y = self.nrow - 1  # 记录当前智能体位置的纵坐标def step(self, action):  # 外部调用这个函数来改变当前位置# 4种动作, change[0]:上, change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)定义在左上角change = [[0, -1], [0, 1], [-1, 0], [1, 0]]self.x = min(self.ncol - 1, max(0, self.x + change[action][0]))self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))next_state = self.y * self.ncol + self.xreward = -1     # 获取当前位置的奖励done = False    # 是否结束if self.y == self.nrow - 1 and self.x > 0:  # 下一个位置在悬崖或者目标done = Trueif self.x != self.ncol - 1:reward = -100return next_state, reward, done

如下所示，ooo区域表示智能体可行走的路径，而****区域表示悬崖，EEEE区域表示目标点。智能体目标是避开悬崖区域****到达右下角终点EEEE。

ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo ooo> ovoo 
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo 
^ooo ooo> ooo> ooo> ^ooo ^ooo ooo> ^ooo oo<o ooo> ooo> ovoo 
^ooo **** **** **** **** **** **** **** **** **** **** EEEE

接下来我们实现sarsa算法，主要功能包括：

初始化：创建Q表、设置学习率α、折扣因子γ和ε-贪婪策略参数。
动作选择：通过ε-贪婪策略选择下一步动作。
最优动作：找出当前状态下的最优动作用于策略展示。
更新规则：根据时序差分误差更新Q值，实现在线策略学习。

# Sarsa 
class Sarsa:""" Sarsa算法 """def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格  存储状态-动作值self.n_action = n_action  # 动作个数self.alpha = alpha  # 学习率self.gamma = gamma  # 折扣因子self.epsilon = epsilon  # epsilon-贪婪策略中的参数def take_action(self, state):  # 选取下一步的操作,具体实现为epsilon-贪婪if np.random.random() < self.epsilon:       # 以ε的概率随机选择一个动作action = np.random.randint(self.n_action)else:           # 以(1-ε)的概率选择当前状态下Q值最大的动作action = np.argmax(self.Q_table[state])return actiondef best_action(self, state):  # 用于打印策略policy   找出给定状态下所有最优动作Q_max = np.max(self.Q_table[state])a = [0 for _ in range(self.n_action)]for i in range(self.n_action):  # 若两个动作的价值一样,都会记录下来if self.Q_table[state, i] == Q_max:a[i] = 1return adef update(self, s0, a0, r, s1, a1):td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]     # 计算时序差分误差(TD error)：当前奖励加上下一个状态-动作对的折扣Q值，减去当前状态-动作对的Q值self.Q_table[s0, a0] += self.alpha * td_error       # 使用学习率α和TD误差更新当前状态-动作对的Q值def print_agent(agent, env, action_meaning, disaster=[], end=[]):for i in range(env.nrow):for j in range(env.ncol):if (i * env.ncol + j) in disaster:print('****', end=' ')elif (i * env.ncol + j) in end:print('EEEE', end=' ')else:a = agent.best_action(i * env.ncol + j)pi_str = ''for k in range(len(action_meaning)):pi_str += action_meaning[k] if a[k] > 0 else 'o'print(pi_str, end=' ')print()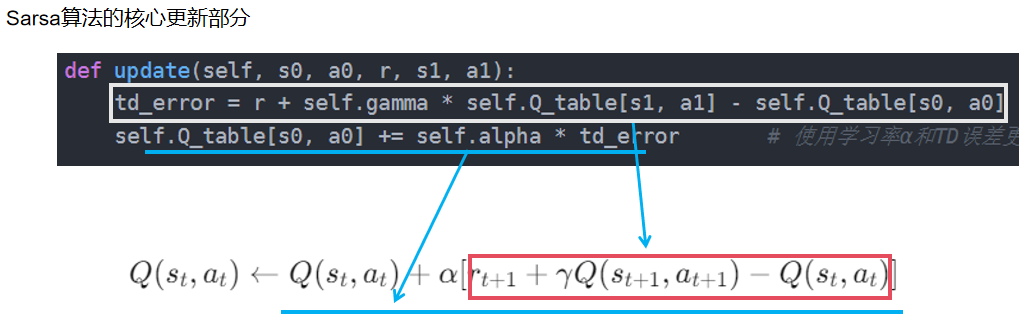

接下来我们进行训练，主要功能包括：初始化环境与智能体参数，通过多轮 episode 训练智能体，记录并绘制回报曲线，最后打印收敛策略。

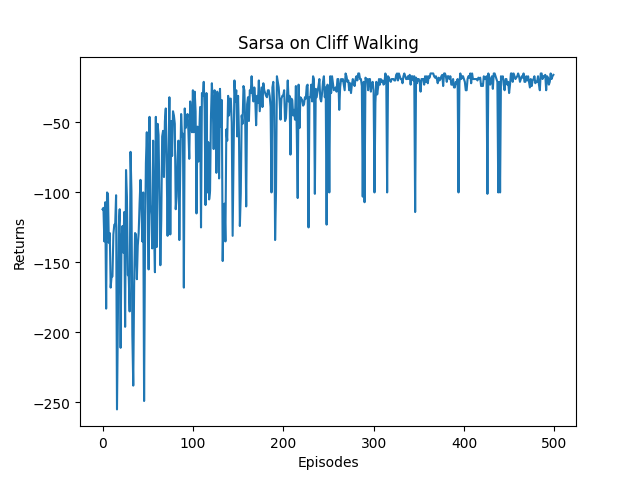
if __name__ == '__main__':ncol = 12nrow = 4env = CliffWalkingEnv(ncol, nrow)       # 创建悬崖环境np.random.seed(0)epsilon = 0.1 # 0.1/0.9/0.01alpha = 0.1 # 0.1/0.05/0.3gamma = 0.9 # 0.9/0.98/0.8agent = Sarsa(ncol, nrow, epsilon, alpha, gamma)    # 创建Sarsa算法对象num_episodes = 500  # 智能体在环境中运行的序列的数量return_list = []  # 记录每一条序列的回报for i in range(10):  # 显示10个进度条# tqdm的进度条功能with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数episode_return = 0state = env.reset()action = agent.take_action(state)       # 智能体根据当前状态选择一个动作done = Falsewhile not done:next_state, reward, done = env.step(action)     # 环境交互：智能体在环境中执行动作并观察结果next_action = agent.take_action(next_state)     # 策略执行：根据当前状态选择下一个动作episode_return += reward  # 这里回报的计算不进行折扣因子衰减agent.update(state, action, reward, next_state, next_action)    # 更新智能体的策略参数state = next_stateaction = next_actionreturn_list.append(episode_return)if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('Sarsa on {}'.format('Cliff Walking'))plt.show()action_meaning = ['^', 'v', '<', '>']print(f"epsilon：{epsilon}\talpha：{alpha}\tgamma：{gamma}")print('Sarsa算法最终收敛得到的策略为：')print_agent(agent, env, action_meaning, list(range(37, 47)), [47])

最终的奖励变化图为：

其中，读者可自行调整epsilon、alpha、gamma

关键结论：

epsilon
- epsilon 越大，智能体就越“随机”，越倾向于探索（exploration）；
- epsilon 越小，智能体就越“贪心”，越倾向于利用（exploitation）它已经学到的最优动作。
- 实际做法往往是让 epsilon 随训练步数衰减（从较大值逐渐降到很小），前期多探索，后期多利用。
alpha
- 调大 alpha 新样本的权重更大，旧值迅速被遗忘收敛快，但波动大；
- 调小 alpha 新样本的权重很小，旧值保留更多波动小，更稳定，容易收敛到平滑曲线；
gamma
- 调大 gamma → 接近 1：未来奖励几乎不打折，远期的回报和眼前一样重要智能体变得更有“耐心”，愿意为了长期大利而忍受短期损失；策略趋向全局最优。但无限期任务下，Q 值可能不收敛（除非 episodic 且终止状态确定）
- 调小 gamma → 接近 0：未来奖励快速衰减，只有即时奖励算数智能体变得**“短视”，只抓眼前最大奖励**；策略趋向即时贪婪。只看当前奖励，退化成贪心策略，完全忽略长期影响

多步Sarsa算法

多步SARSA（Multi-step SARSA）和单步SARSA（One-step SARSA）是SARSA算法的两种变体，它们在更新Q值时考虑的未来奖励步数不同。这两种方法的主要区别在于它们如何计算TD误差和更新Q值。

多步SARSA考虑了多步未来的回报来更新Q值。它不是在每个时间步都更新Q值，而是在固定数量的步骤后更新，或者直到达到终止状态。更新规则如下： $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha [G_{t:t+n} - Q(s_t, a_t)]$ 。其中 $G_{t:t+n}$ 是从时间 t 到 t+n 的累积折扣回报，即 $G_{t:t+n} = r_{t+1} + \gamma r_{t+2} + \cdots + \gamma^{n-1} r_{t+n} + \gamma^n V(s_{t+n})$ ， $V(s_{t+n})$ 是状态 $s_{t+n}$ 的价值函数。

代码

multi-Sarsa只需要更改sarsa部分即可。

这段代码实现了n步Sarsa算法，用于强化学习中的策略优化。主要功能包括：

初始化：创建Q表、存储状态、动作和奖励的列表。
动作选择：根据ε-贪婪策略选择动作。
策略输出：返回当前状态下最优动作。
更新机制：
1. 每次交互保存状态、动作、奖励；
2. 当积累n步后，计算n步回报并更新Q值；
3. 若到达终止状态，则清空历史记录。

# multi-Sarsa 
class nstep_Sarsa:""" n步Sarsa算法 """def __init__(self, n, ncol, nrow, epsilon, alpha, gamma, n_action=4):self.Q_table = np.zeros([nrow * ncol, n_action])self.n_action = n_actionself.alpha = alphaself.gamma = gammaself.epsilon = epsilonself.n = n  # 采用n步Sarsa算法self.state_list = []  # 保存之前的状态self.action_list = []  # 保存之前的动作self.reward_list = []  # 保存之前的奖励def take_action(self, state):if np.random.random() < self.epsilon:action = np.random.randint(self.n_action)else:action = np.argmax(self.Q_table[state])return actiondef best_action(self, state):  # 用于打印策略Q_max = np.max(self.Q_table[state])a = [0 for _ in range(self.n_action)]for i in range(self.n_action):if self.Q_table[state, i] == Q_max:a[i] = 1return adef update(self, s0, a0, r, s1, a1, done):self.state_list.append(s0)self.action_list.append(a0)self.reward_list.append(r)if len(self.state_list) == self.n:  # 若保存的数据可以进行n步更新G = self.Q_table[s1, a1]  # 得到Q(s_{t+n}, a_{t+n})for i in reversed(range(self.n)):G = self.gamma * G + self.reward_list[i]  # 不断向前计算每一步的回报# 如果到达终止状态,最后几步虽然长度不够n步,也将其进行更新if done and i > 0:s = self.state_list[i]a = self.action_list[i]self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])s = self.state_list.pop(0)  # 将需要更新的最初的状态动作从列表中删除,下次不必更新a = self.action_list.pop(0)self.reward_list.pop(0)# n步Sarsa的主要更新步骤self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])     # 根据n步后的值，更新最初的状态动作对Qif done:  # 如果到达终止状态,即将开始下一条序列,则将列表全清空self.state_list = []self.action_list = []self.reward_list = []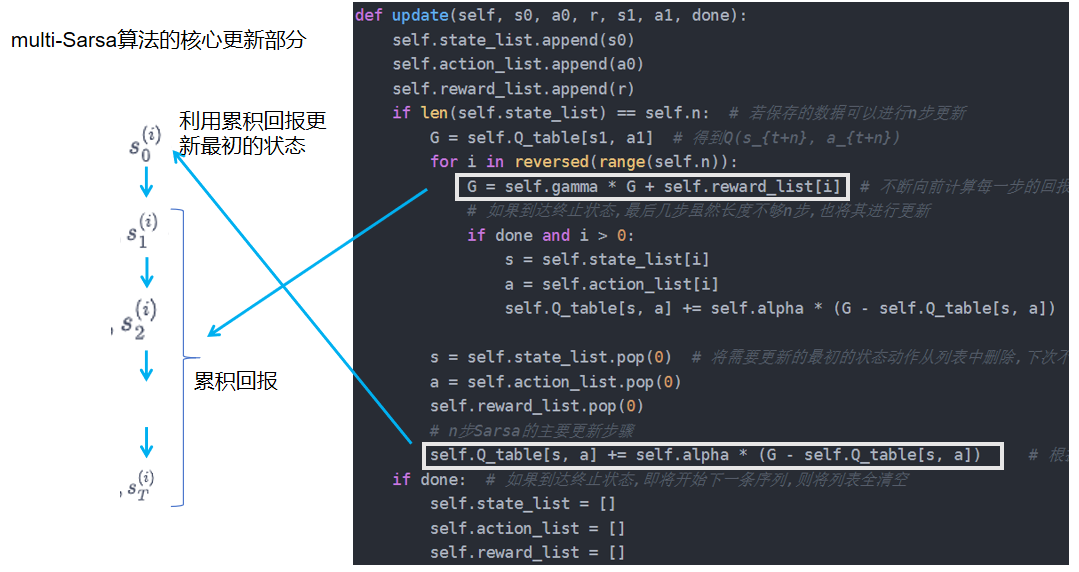

接下来我们进行训练

if __name__ == '__main__':np.random.seed(0)ncol = 12nrow = 4env = CliffWalkingEnv(ncol, nrow)n_step = 5  # 5步Sarsa算法alpha = 0.1epsilon = 0.1gamma = 0.9agent = nstep_Sarsa(n_step, ncol, nrow, epsilon, alpha, gamma)num_episodes = 500  # 智能体在环境中运行的序列的数量return_list = []  # 记录每一条序列的回报for i in range(10):  # 显示10个进度条#tqdm的进度条功能with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数episode_return = 0state = env.reset()action = agent.take_action(state)done = Falsewhile not done:next_state, reward, done = env.step(action)next_action = agent.take_action(next_state)episode_return += reward  # 这里回报的计算不进行折扣因子衰减agent.update(state, action, reward, next_state, next_action,done)state = next_stateaction = next_actionreturn_list.append(episode_return)if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('5-step Sarsa on {}'.format('Cliff Walking'))plt.show()action_meaning = ['^', 'v', '<', '>']print('5步Sarsa算法最终收敛得到的策略为：')print_agent(agent, env, action_meaning, list(range(37, 47)), [47])

其奖励变化情况如下：

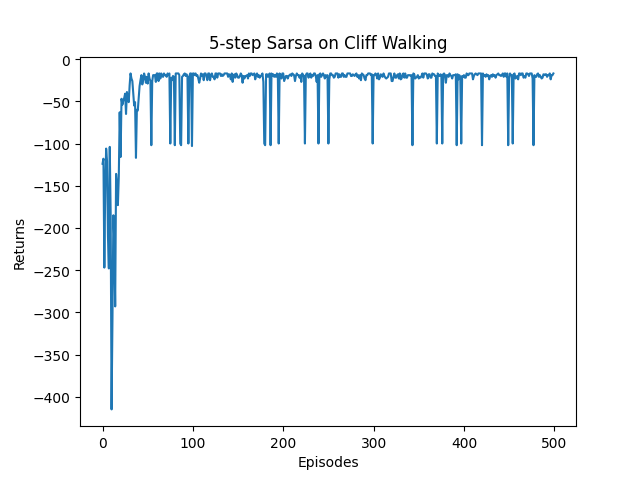
Q-Learning算法

最大区别在于 Q-learning 的时序差分更新方式为 $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha [R_t + \gamma \max_a Q(s_{t+1}, a) - Q(s_t, a_t)]$

SARSA的更新规则：根据当前策略选择的下一个动作来更新Q值
Q-Learning更新规则：选择所有可能动作的最大Q值来更新，该动作不一定是策略选择的动作。

换句话说：sarsa是一种同步更新策略，而Q-Learning是一种异步更新策略。

Q-Learning的伪代码：

在线策略和离线策略

称采样数据的策略为行为策略（behavior policy），称用这些数据来更新的策略为目标策略（target policy）。

在线策略（on-policy）算法表示行为策略和目标策略是同一个策略；而离线策略（off-policy）算法表示行为策略和目标策略不是同一个策略。Sarsa 是典型的在线策略算法，而 Q-learning 是典型的离线策略算法。

代码

同样只需要更改sarsa部分即可。这段代码实现了Q-learning算法。初始化Q表、学习率等参数；[take_action]根据ε-贪婪策略选择动作；[best_action]返回当前状态下的最优动作；[update]通过时序差分更新Q值。

class QLearning:""" Q-learning算法 """def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格self.n_action = n_action  # 动作个数self.alpha = alpha  # 学习率self.gamma = gamma  # 折扣因子self.epsilon = epsilon  # epsilon-贪婪策略中的参数def take_action(self, state):  #选取下一步的操作if np.random.random() < self.epsilon:action = np.random.randint(self.n_action)else:action = np.argmax(self.Q_table[state])return actiondef best_action(self, state):  # 用于打印策略Q_max = np.max(self.Q_table[state])a = [0 for _ in range(self.n_action)]for i in range(self.n_action):if self.Q_table[state, i] == Q_max:a[i] = 1return adef update(self, s0, a0, r, s1):td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]       # 计算时序差分误差(TD error)：当前奖励加上下一个状态的最大Q值的折扣，减去当前状态-动作对的Qself.Q_table[s0, a0] += self.alpha * td_error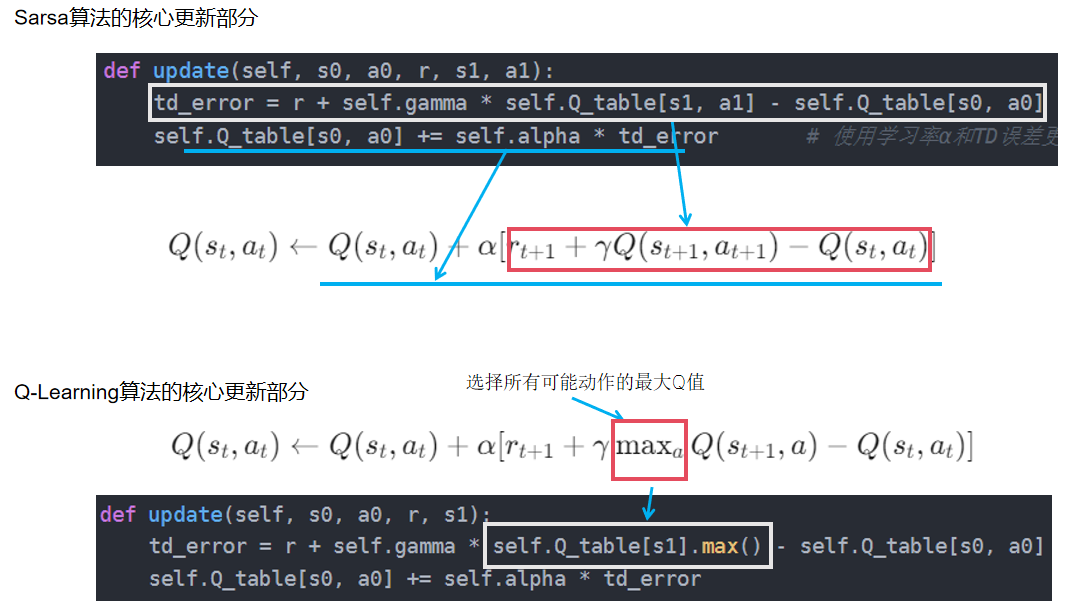

接下来我们进行训练

if __name__ == '__main__':ncol = 12nrow = 4env = CliffWalkingEnv(ncol, nrow)np.random.seed(0)epsilon = 0.1alpha = 0.1gamma = 0.9agent = QLearning(ncol, nrow, epsilon, alpha, gamma)num_episodes = 500  # 智能体在环境中运行的序列的数量return_list = []  # 记录每一条序列的回报for i in range(10):  # 显示10个进度条# tqdm的进度条功能with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数episode_return = 0state = env.reset()done = Falsewhile not done:action = agent.take_action(state)next_state, reward, done = env.step(action)episode_return += reward  # 这里回报的计算不进行折扣因子衰减agent.update(state, action, reward, next_state)state = next_statereturn_list.append(episode_return)if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('Q-learning on {}'.format('Cliff Walking'))plt.show()action_meaning = ['^', 'v', '<', '>']print('Q-learning算法最终收敛得到的策略为：')print_agent(agent, env, action_meaning, list(range(37, 47)), [47])

其奖励变化情况如下：

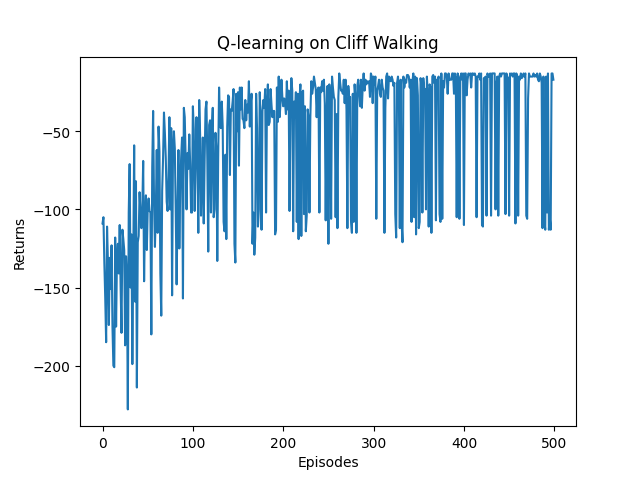
基于模型的强化学习

根据是否具有环境模型，强化学习算法分为两种：基于模型的强化学习（model-based reinforcement learning）和无模型的强化学习（model-free reinforcement learning）。

基于模型的强化学习算法由于具有一个环境模型，智能体可以额外和环境模型进行交互，对真实环境中样本的需求量往往就会减少，因此通常会比无模型的强化学习算法具有更低的样本复杂度。但是，环境模型可能并不准确，不能完全代替真实环境，因此基于模型的强化学习算法收敛后其策略的期望回报可能不如无模型的强化学习算法。

Dyna-Q 算法是一个经典的基于模型的强化学习算法。Dyna-Q 使用一种叫做 Q-planning 的方法来基于模型生成一些模拟数据，然后用模拟数据和真实数据一起改进策略。Q-planning 每次选取一个曾经访问过的状态，采取一个曾经在该状态下执行过的动作，根据这个模拟数据（s,a,r,s’），用 Q-learning 的更新方式来再次更新动作价值函数。

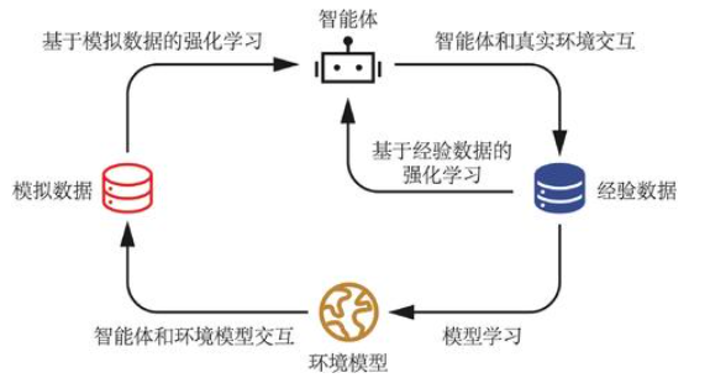
代码

这段代码实现了Dyna-Q算法，结合了Q-learning与环境模型学习。主要功能包括：

init：初始化Q表、参数及空模型。
take_action：依ε-贪婪策略选择动作。
q_learning：执行一次Q-learning更新。
update：先进行实际经验的Q-learning更新，再通过环境模型生成模拟经验，多次迭代更新Q值，提升学习效率。

class DynaQ:""" Dyna-Q算法 """def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_planning, n_action=4):self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格self.n_action = n_action  # 动作个数self.alpha = alpha  # 学习率self.gamma = gamma  # 折扣因子self.epsilon = epsilon  # epsilon-贪婪策略中的参数self.n_planning = n_planning  #执行Q-planning的次数, 对应1次Q-learningself.model = dict()  # 环境模型def take_action(self, state):  # 选取下一步的操作if np.random.random() < self.epsilon:action = np.random.randint(self.n_action)else:action = np.argmax(self.Q_table[state])return actiondef q_learning(self, s0, a0, r, s1):td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]self.Q_table[s0, a0] += self.alpha * td_errordef update(self, s0, a0, r, s1):self.q_learning(s0, a0, r, s1)      # 先进行实际经验的Q-learning更新self.model[(s0, a0)] = r, s1        # 将数据添加到模型中for _ in range(self.n_planning):    # Q-planning循环# 随机选择曾经遇到过的状态动作对进行模拟的Q-learning更新(s, a), (r, s_) = random.choice(list(self.model.items()))self.q_learning(s, a, r, s_)        # 使用模型中的模拟经验进行Q-learning更新(相当于每次比q-learning多更新若干次)

接下来我们展示不同Q-planning的效果：

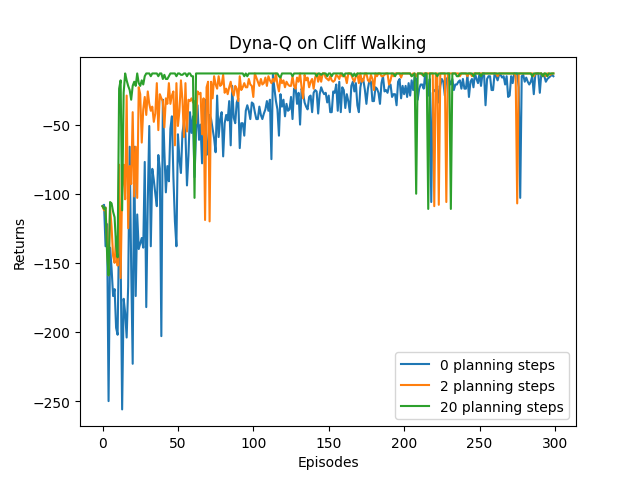
def DynaQ_CliffWalking(n_planning):ncol = 12nrow = 4env = CliffWalkingEnv(ncol, nrow)epsilon = 0.01alpha = 0.1gamma = 0.9agent = DynaQ(ncol, nrow, epsilon, alpha, gamma, n_planning)num_episodes = 300  # 智能体在环境中运行多少条序列return_list = []  # 记录每一条序列的回报for i in range(10):  # 显示10个进度条# tqdm的进度条功能with tqdm(total=int(num_episodes / 10),desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数episode_return = 0state = env.reset()done = Falsewhile not done:action = agent.take_action(state)next_state, reward, done = env.step(action)episode_return += reward  # 这里回报的计算不进行折扣因子衰减agent.update(state, action, reward, next_state)state = next_statereturn_list.append(episode_return)if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)return return_listif __name__ == '__main__':np.random.seed(0)random.seed(0)n_planning_list = [0, 2, 20]for n_planning in n_planning_list:print('Q-planning步数为：%d' % n_planning)time.sleep(0.5)return_list = DynaQ_CliffWalking(n_planning)episodes_list = list(range(len(return_list)))plt.plot(episodes_list,return_list,label=str(n_planning) + ' planning steps')plt.legend()plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('Dyna-Q on {}'.format('Cliff Walking'))plt.show()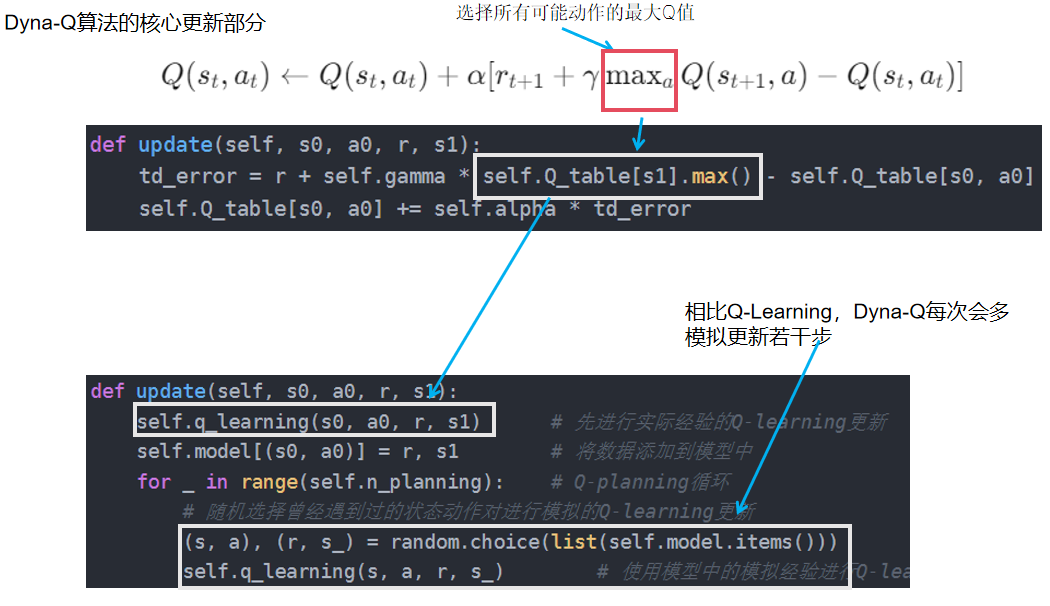

总结

强化学习是一种人工智能范式，它让智能体在未知环境中通过试错自我进化，目标是最大化长期回报。其核心机制是基于“状态 - 动作 - 奖励”的闭环：智能体观察当前状态，根据策略选择一个动作，环境会立即返回一个标量奖励并转移到下一个状态。与监督学习不同，强化学习不需要预先提供样本标签，而是让智能体在与环境的动态交互中探索有效路径，同时利用已有经验避免重复无效尝试，平衡“探索”与“利用”是其关键挑战之一。

强化学习的关键概念包括马尔科夫决策过程（MDP），它假设系统的下一刻状态只依赖当前状态和动作，与历史无关。此外，折扣累积奖励是通过折扣因子对未来的奖励进行加权求和，以计算长期回报。价值函数也是强化学习中的重要概念，其中状态价值函数表示从某个状态开始并遵循策略所能获得的期望回报，而动作价值函数则描述了在某个状态下采取某个动作后所获得的期望回报。

在强化学习算法方面，无模型的强化学习不需要事先知道环境的奖励函数和状态转移函数，而是直接通过与环境交互学习。蒙特卡洛方法基于完整的采样轨迹来估计价值函数，而时序差分（TD）学习则利用TD误差在线更新价值函数。Sarsa算法是一种时序差分学习算法，通过与环境交互学习策略，并采用ε - 贪婪策略在探索和利用之间取得平衡。Q - Learning算法是一种离线策略算法，选择所有可能动作的最大Q值来更新。多步Sarsa算法考虑多步未来的回报来更新Q值，比单步Sarsa更高效。Dyna - Q算法结合了Q - learning和环境模型学习，通过Q - planning生成模拟数据来改进策略。

在实现与应用方面，可以通过定义环境类来模拟特定的任务场景，例如悬崖行走环境。训练过程包括通过多轮episode训练智能体，记录并绘制回报曲线，以及打印收敛策略。在训练过程中，参数的调整也非常关键，例如ε（epsilon）控制探索与利用的平衡，α（alpha）是学习率，影响新样本的权重，而γ（gamma）是折扣因子，影响未来奖励的权重。

总的来说，强化学习通过智能体与环境的交互来学习最优策略，关键在于平衡探索与利用，以及通过价值函数来评估状态和动作的价值。不同的算法在更新策略和利用环境模型方面各有特点，适用于不同的场景和需求。通过调整参数和选择合适的算法，可以有效提高智能体的学习效率和策略性能。

查看全文

http://www.dtcms.com/a/439930.html