当前位置：首页 > news >正文

654.最大二叉树（二叉树算法）

news 2025/10/4 13:44:33

654.最大二叉树

力扣题目地址

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

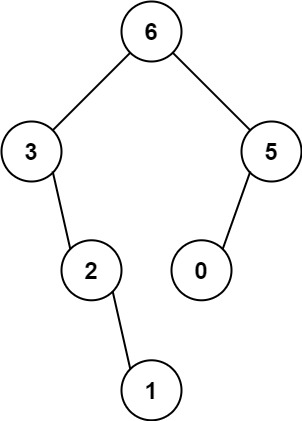
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。- 空数组，无子节点。- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。- 空数组，无子节点。- 只有一个元素，所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。- 只有一个元素，所以子节点是一个值为 0 的节点。- 空数组，无子节点。

示例 2：

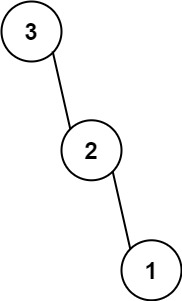
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {/*** 主函数：构造最大二叉树* * @param nums 输入数组* @return 构造出的最大二叉树的根节点*/public TreeNode constructMaximumBinaryTree(int[] nums) {// 启动递归构建过程// 使用左闭右开区间 [0, nums.length)return constructMaximumBinaryTree1(nums, 0, nums.length);}/*** 递归函数：在 nums[leftIndex, rightIndex) 范围内构造最大二叉树* * @param nums       原始数组* @param leftIndex  子数组起始索引（包含）* @param rightIndex 子数组结束索引（不包含）* @return 当前子数组构造出的最大二叉树的根节点*/public TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {// 递归终止条件1：区间为空（左闭右开）if (rightIndex - leftIndex < 1) {return null;}// 递归终止条件2：区间只有一个元素if (rightIndex - leftIndex == 1) {return new TreeNode(nums[leftIndex]); // 直接创建叶子节点}// 在当前区间 [leftIndex, rightIndex) 中寻找最大值及其索引int maxIndex = leftIndex;           // 记录最大值的索引int maxVal = nums[leftIndex];       // 记录最大值// 遍历区间，从 leftIndex+1 开始比较for (int i = leftIndex + 1; i < rightIndex; i++) {if (nums[i] > maxVal) {maxVal = nums[i];maxIndex = i;}}// 创建当前子树的根节点（即当前区间的最大值）TreeNode root = new TreeNode(maxVal);// 递归构建左子树：// 范围是 [leftIndex, maxIndex) —— 最大值左侧的子数组root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);// 递归构建右子树：// 范围是 [maxIndex + 1, rightIndex) —— 最大值右侧的子数组root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);// 返回当前子树的根节点return root;}
}

🔑 核心思路与关键点总结

1. 核心思想

分治 + 递归：每次在当前数组区间中找到最大值作为根，然后递归处理左右子数组。
构造规则明确：根 = 区间最大值，左子树 = 左侧子数组构造的树，右子树 = 右侧子数组构造的树。

🔄 这是一个典型的“以最大值为分割点”的递归构造问题。

2. 关键步骤

步骤	说明
✅ 1. 确定当前区间的最大值	遍历 `[leftIndex, rightIndex)` 找最大值及其索引
✅ 2. 创建根节点	用最大值 `maxVal` 构造 `TreeNode`
✅ 3. 划分左右子数组	- 左：`[leftIndex, maxIndex)` - 右：`[maxIndex+1, rightIndex)`
✅ 4. 递归构建左右子树	分别对左右子数组递归调用构造函数
✅ 5. 连接并返回根	将左右子树挂到根节点上，返回根

3. 区间设计：左闭右开 `[leftIndex, rightIndex)`

这是 Java 中常见的区间表示方式（如 Arrays.copyOfRange）。
优点：
- 区间长度 = rightIndex - leftIndex
- 空区间判断：rightIndex - leftIndex < 1
- 单元素区间：== 1，直接返回
- 切分自然，避免 +1/-1 错误

4. 递归终止条件

条件	说明
`rightIndex - leftIndex < 1`	空区间，返回 `null`
`== 1`	单个元素，直接创建叶子节点返回

⚠️ 注意：虽然 == 1 可以被包含在后续逻辑中处理，但单独判断可减少一次循环，略微优化性能。

5. 时间与空间复杂度

项目	复杂度	说明
时间复杂度	O(n²) 最坏，O(n log n) 平均	每层递归都要遍历找最大值。最坏情况（递减数组）退化为链表，每层找最大值 O(n)，共 n 层 → O(n²)；平均情况类似快排，O(n log n)
空间复杂度	O(n)	递归栈深度最坏 O(n)（链状树），平均 O(log n)

💡 提示：可以通过线段树预处理将找最大值优化到 O(1)，从而将总时间优化到 O(n)，但面试中一般不要求。

6. 易错点提醒

错误	说明
❌ 区间开闭混淆	比如右子树写成 `maxIndex` 而不是 `maxIndex+1`，会导致重复使用最大值
❌ 忘记处理空区间	导致数组越界或无限递归
❌ 找最大值时初始值设置错误	如 `maxIndex = 0` 而不是 `leftIndex`，会越界
❌ 循环范围错误	应为 `i < rightIndex`，不能写成 `<=`