时间复杂度的题型梳理和方法总结

前言

对于这类时间复杂度的题型一般是4分 即选择题两分 代码题两分 只不过一个是题目丢给我们一个代码块让我们去分析时间复杂度 另一个是根据自己写的代码 学会去分析时间复杂度 本篇文章基本是对于前者的题型总结和思路梳理 因为考场上大家写代码题基本都是暴力解法 循环变量的更新都是线性递增的 基本很容易就能看出来是O（n）或者O（n^2）所以我觉得这个虽然灵活程度高但是比较代码是自己写的 知根知底 对吧

单层循环

思路分析

• 此类问题也是最简单的一种 因为只有一个变量 那么我们只需要去关注它什么时候突破限制就好 所以我们一般会采用设“t”法 什么意思呢 我们假设一共进行t轮循环
• 在这之后我们首先得弄清楚规律 什么规律呢 就是研究的变量 它变化的规律
• 那在这之后就自然而然的得到了第T轮的情况
• 我们只需要让它突破这个限制（>=）那么就可以知道最多进行多少轮循环
• 这样做的根本目的就是得到我们的t和输入的参数n之间的关系 从而得到我们的数量级

实操演示

递归

思路分析

• 对于递归类的题目我们是找不到循环的 那它怎么来写呢
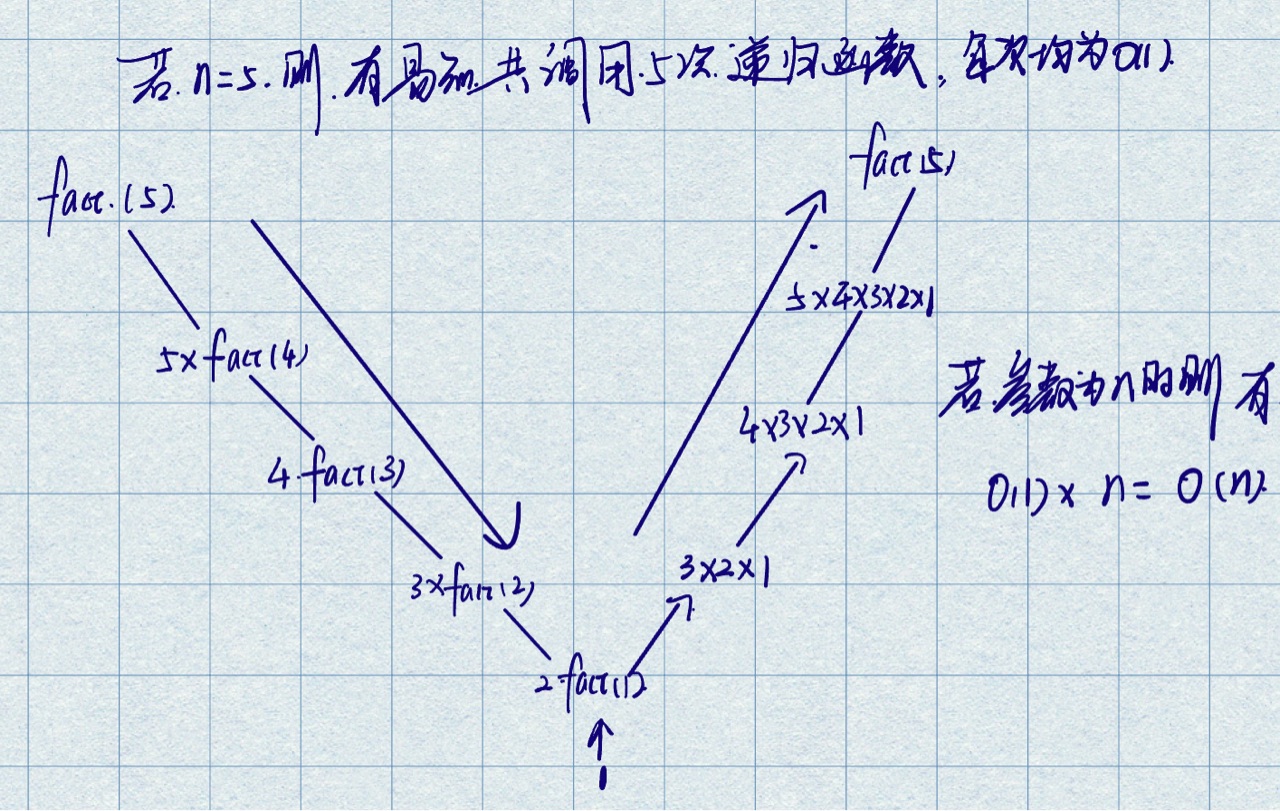
• 基本思路就是我们需要求出递归的深度 或者说调用递归函数的次数再去乘以每个递归函数的时间复杂度
• 这是一个递推回归的过程 也是递归的本质

实操演练

双层循环

由于这里涉及到两个循环变量 我们既然要探究问题规模n与时间复杂度的关系 那么我们自然就需要考虑这两个变量是否具有联系 如果层层无关 那么我们就可以独立的进行计算 如果有联系我们就需要综合考虑 因为内层的循环次数取决于外层变量的值

循环变量无关

基本思路

• 计算出各层的时间复杂度 然后相乘即可
• 本质上的原因就是只要外层每变化一次内层都是循环一样的次数 并且完全不依赖于外层变量
• 所以拆开算是一点问题都没有的
• 其实我说一个东西大家应该都可以理解了 就是二重积分 当积分上下限都是常数被积函数可拆的情况之下完全可以拆成两个定积分相乘 原理我觉得大致相同

实操演示

甚至都懒得写 内层一眼O（n）外层O（logn） 乘机不就是 O（nlogn）

循环变量相关

• 这是我们近年来考试的重点 这也是最综合的一类题型

基本思路

• 首先我们需要明确的是这种情况之下我们就不能够按照之前那么来算了而是需要综合考虑
• 因为外层的循环因子会影响内层的循环次数
• 具体怎么来做呢 下面我来演示一下

实操演示

• 2022 408真题
  (https://i-blog.csdnimg.cn/direct/ece2fb3661d84f189f5a6223e58f45fc.png)

• 例题2 （2025年）

• 对于这道题目的分析思路基本是跟上面一致的

结语

这个部分大部分是在408试卷的第一题的位置上 虽然大部分时候在整张试卷仅仅占两分 但是我觉得这两分只要你弄懂之后是非常好拿的 所以我觉得画个半小时学一下还是值得的 并且有助于数据结构代码题的学习