基于最小和算法的QC-LDPC 译码器的FPGA 实现（一）

        本文介绍一种层间流水线结构的译码器，并以FPGA 作为实现平台， 以WIMAX 标准(2304，1152)QC-LDPC码为例，设计仿真了基于最小和算法的QC-LDPC码译码器，并提高了吞吐率。

1 QC-LDPC 码的校验矩阵

        QC-LDPC 码的校验矩阵是由一组循环子矩阵构成，子矩阵具有如下特点：
1) 每一个子矩阵都是一个n×n 大小的方阵；
2) 循环子矩阵的任意一行(列) 都是由上一行(列) 向右(下) 移动一位得到的，特别的，循环
子矩阵的第一行(列) 由循环子矩阵的最后一行(列) 向右(下) 移动一位得到。
QC-LDPC 码的校验矩阵可定义为

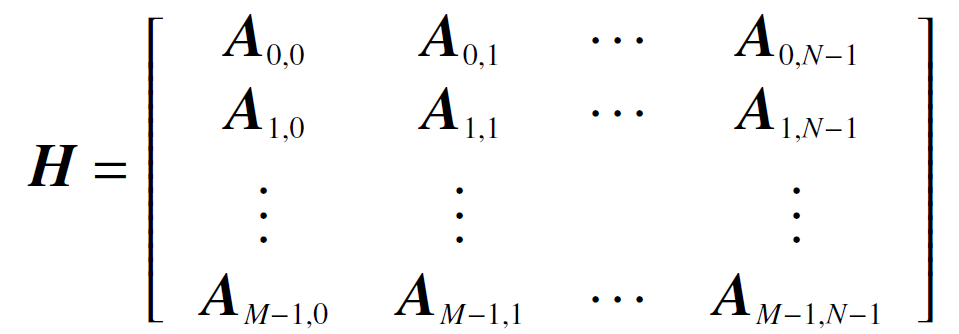
式中：M，N 为正整数，是n×n 大小的子矩阵，由全零矩阵或单位循环移位矩阵组成。由上式可知， QC-LDPC 码的校验矩阵由M×N 个n×n 大小单位循环方阵组成。WIMAX 标准(2304，1152)
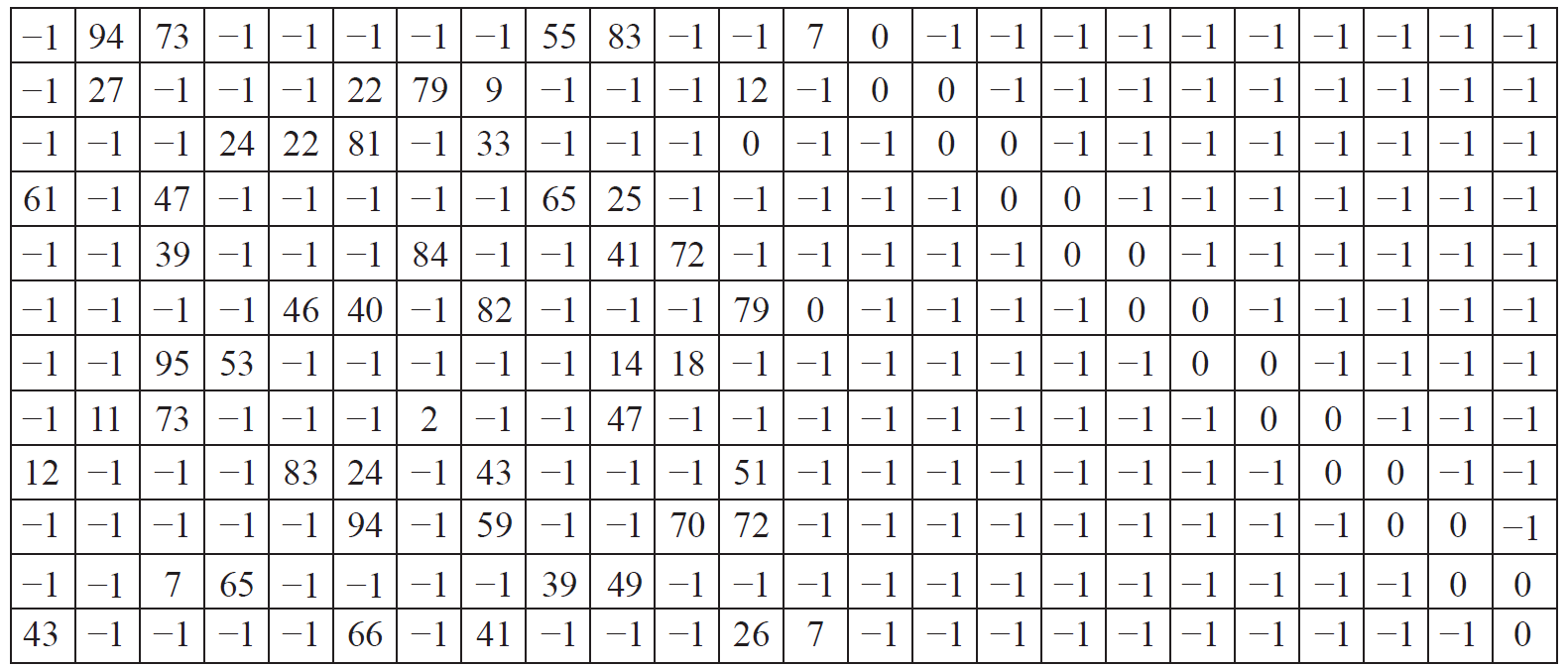
QC-LDPC 码的基矩阵如图所示。

2 QC-LDPC 码的分层最小和译码算法

分层最小和译码算法是分层算法与最小和算法的结合。

        最小和算法是BP译码算法的简化版本，对校验节点传递给变量节点的对数似然比概率信息进行近似运算，该算法不需要信道估计， 将复杂的双曲正切运算转化为比较(取最小) 运算和加法运算，与BP 译码算法相比大大减少了计算量，降低了硬件实现难度。

        分层算法则是将校验矩阵H以行为基准分为若干层，每层列重最大为1。

        首先基于第一层进行校验信息的更新；其次将更新后的校验信息代入到变量节点中进行变量信息的更新，当第一层信息更新完成后，即将更新后的信息传递给下一层，继续进行下一层的校验信息和变量信息的更新，直至所有分层都完成信息的更新；最后对得到的后验概率信息进行硬判决并进行校验，如符合判决条件则停止译码，不符合则重新开始直至符合判决条件。

        在非分层算法中，信息是双向传递的，变量节点需要等待校验节点完全更新后才能开始更新，反之亦然。

        而在分层算法中的变量信息是用后验概率信息与校验信息来表示的，因此无需储存变量信息；横向更新使用的信息都是上一行或上一次迭代纵向更新的信息。

分层译码算法与非分层算法相比，减少了单次迭代所需时间，信息迭代过程中分层译码算法简化了储存器与数据交换网络，降低译码复杂度和链路延时。

        具体分层最小和译码算法如下：

1) 初始化

        利用初始信道信息解调后得到的对数似然比序列对后验概率信息进行初始化：

式中： 表示第一次迭代时各校验节点的信息；表示初始信道信息解调后得到的对数似然比序列。

2) 分层更新

        ①根据上一层得到的后验概率信息和校验节点信息更新变量节点信息：

        式中：n 为当前迭代次数；m 为当前层数。
②根据更新后的变量节点信息更新当前层的校验节点信息：

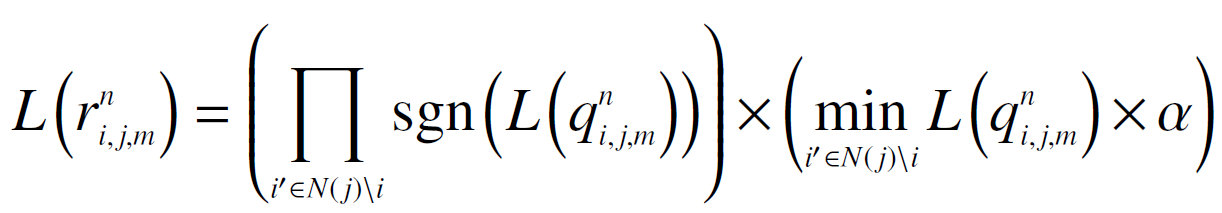
        式中α 为归一化因子，是一个小于1 的常数。
③根据更新后的变量节点信息与校验节点信息更新后验概率信息，作为下一层的后验概率信息：

        式中m=m+1，重复步骤①~③，直至最后一层。

3) 译码判决

        对进行硬判决译码： 若， 则；若，则。

        将矩阵H与序列相乘得到校验结果，若校验结果为0 或者达到最大迭代次数，停止迭代；若
校验结果不为0 且未达到最大迭代次数，重复步骤2)、3)。