当前位置：首页 > news >正文

【AI论文】基于分位数优势估计的熵安全推理方法

news 2025/10/3 12:56:35

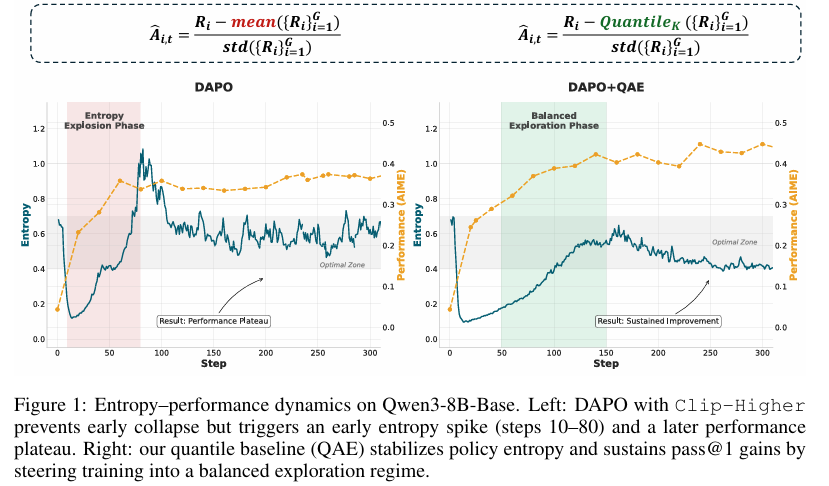
摘要：可验证奖励的强化学习（Reinforcement Learning with Verifiable Rewards, RLVR）虽能增强大语言模型（LLM）的推理能力，但其训练过程常在熵崩溃与熵爆炸两种极端状态间振荡。我们追溯发现，这两种风险均源于无价值函数强化学习（如GRPO和DAPO）中采用的均值基线方法——该方法在奖励异常值情况下会对负优势样本施加不当惩罚。为此，我们提出分位数优势估计（Quantile Advantage Estimation, QAE），以组级K分位数基线替代均值基线。QAE构建了响应层面的双模式门控机制：对于困难查询（概率p ≤ 1 - K），强化罕见成功案例；对于简单查询（概率p > 1 - K），则聚焦剩余失败案例。通过一阶softmax更新，我们证明了QAE具有双边熵安全性，即对单步熵变化给出上下界约束，从而抑制熵爆炸并防止熵崩溃。实证表明，这一微小改进即可稳定熵值、稀疏化信用分配（在调整K值后，约80%的响应获得零优势），并在AIME 2024/2025和AMC 2023基准测试中持续提升Qwen3-8B/14B-Base模型的pass@1指标。这些结果揭示，相较于词元级启发式方法，基线设计才是扩展RLVR性能的核心机制。Huggingface链接：Paper page，论文链接：2509.22611

研究背景和目的

研究背景：

随着大型语言模型（LLMs）在自然语言处理任务中的广泛应用，如何通过强化学习（RL）提升其推理能力成为了一个关键问题。特别是基于可验证奖励的强化学习（RLVR），通过奖励模型的正确性来优化LLMs，使其在数学推理、编程等复杂任务中取得了显著进展。

然而，RLVR在训练过程中常常面临策略熵（policy entropy）的极端波动问题，即熵崩溃（entropy collapse）和熵爆炸（entropy explosion）。熵崩溃指的是策略分布过早地变得过于确定，抑制了探索，从而限制了模型的泛化能力；而熵爆炸则表现为策略变得过于随机，导致学习信号被噪声淹没，训练变得不稳定且效率低下。

在RLVR中，常用的价值自由（value-free）RL方法，如Group Relative Policy Optimization (GRPO) 和 Dynamic Sampling Policy Optimization (DAPO)，通常使用均值基线（mean baseline）来估计优势函数（advantage function）。

然而，这种均值基线对奖励异常值（reward outliers）敏感，可能导致负优势样本（negative-advantage samples）被不当惩罚，进而引发熵崩溃或熵爆炸。

研究目的：

本研究旨在提出一种名为Quantile Advantage Estimation (QAE)的新方法，以解决RLVR中的熵崩溃和熵爆炸问题。

具体目标包括：

稳定策略熵：通过引入K-分位数基线（K-quantile baseline），替代传统的均值基线，以减少异常值对优势估计的影响，从而稳定策略熵。
实现两级熵安全：证明QAE方法能够在训练过程中提供熵的两级安全边界，防止熵崩溃和熵爆炸的发生。
提升任务性能：在多个数学推理基准测试上验证QAE方法的有效性，显著提升LLMs的pass@1和pass@16准确率。

研究方法

1. 问题分析：

研究首先分析了RLVR中熵崩溃和熵爆炸的根源，指出均值基线对奖励异常值的敏感性是导致这一问题的主要原因。

在RLVR中，负优势样本（negative-advantage samples）在训练早期往往占据主导地位，导致策略熵的剧烈波动。

2. QAE方法设计：

为了解决上述问题，QAE方法用K-分位数基线替代了传统的均值基线。具体设计如下：

K-分位数基线：对于每个查询，计算响应组中成功率的K-分位数作为基线。如果成功率p ≤ 1-K，则基线为0；如果p > 1-K，则基线为1。
优势估计：基于K-分位数基线，计算每个响应的优势。对于成功查询（p ≤ 1-K），仅强化罕见成功；对于失败查询（p > 1-K），则针对剩余失败进行优化。
熵安全机制：通过理论分析证明，QAE方法能够在一步更新中提供熵的下界和上界，从而防止熵崩溃和熵爆炸。

3. 实验设计：

实验在三个标准数学推理基准上进行：AIME’24、AIME’25和AMC’23。

所有评估均为零样本（zero-shot）评估，每个查询采样32个完成结果，温度T=0.7。主要评估指标为pass@1和pass@16准确率。