老题新解|再求 f(x,n)

《信息学奥赛一本通》第147题：再求 f(x,n)

题目描述
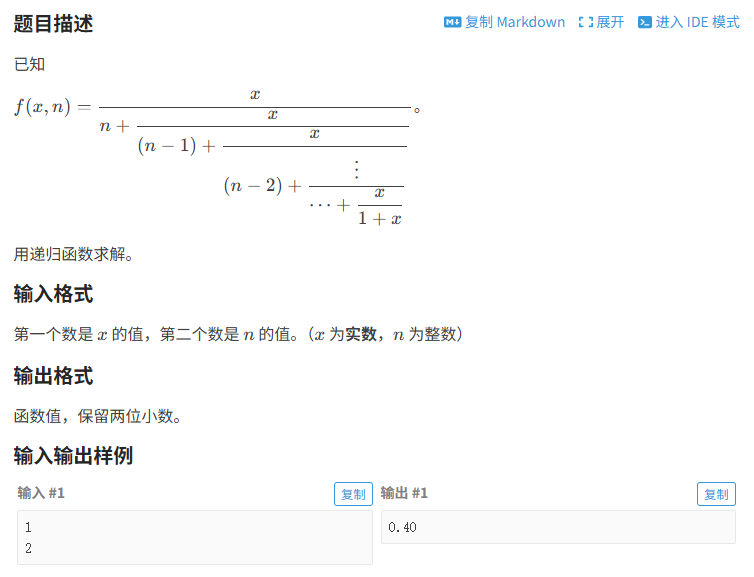
已知
$f(x,n)=\frac{x}{n+\frac{x}{(n-1)+\frac{x}{(n-2)+\frac{⋮}{\cdots +\frac{x}{1+x}}}}}$。
用递归函数求解。
输入格式
第一个数是 $x$ 的值，第二个数是 $n$ 的值。（$x$ 为实数，$n$ 为整数）
输出格式
函数值，保留两位小数。
输入输出样例 #1
输入 #1
1
2
输出 #1
0.40

大家好，我是莫小特。
这篇文章给大家带来《信息学奥赛一本通》中的第 147 题：再求 f(x,n)。

一、题目描述

洛谷的题号是：B2148 再求 f(x,n)

二、题意分析

这道题是信息学奥赛一本通练习题的第 147 题。

根据输入格式的描述，输入两个数，一个是 x，另一个是 n，x 是实数，n 是整数，为避免精度问题，两个都用 double 类型。

double x,n;
cin>>x>>n;

根据题目描述，需要按公式完成式子的计算，先计算第 1 层，即 k=1 时：

$$f(x,1)=\frac{x}{1+x}$$
而对于 k>=2 时，就需要将第 k-1 层的结果放在分母：

$$f(x,k)=\frac{x}{k+f(x,k-1)}$$

所以可以写函数，函数名为 add，根据输出结果，返回类型为 double，参数有两个。

当 n 等于 1 时，返回 $\frac{x}{1+x}$ 值，可以将 1 变为 1.0，方便精度。

当 n 大于 1 时，返回 $\frac{x}{k+f(x,k-1)}$ 值，

double add(double x,double n)
{//边界if(n==1) return x/(1.0+x);else{return x/(n+add(x,n-1.0)); }
}

输出小数点后两位，使用 printf 函数。

printf("%.2lf",add(x,y));

按照样例输入对数据进行验证。

符合样例输出，到网站提交测评。

测试通过！

三、完整代码

该题的完整代码如下：

#include <iostream>
using namespace std;
double add(double x,double n)
{//边界if(n==1) return x/(1+x);else{return x/(n+add(x,n-1)); }
}
int main()
{double x,y;cin>>x>>y;printf("%.2lf",add(x,y));
}

四、总结

本题考察了递归函数与分数嵌套表达式的实现，主要涵盖以下知识点：

1、递归函数设计

（1）明确递归的边界条件：当 n=1 时返回 $\frac{x}{1+x}$。
（2）递归调用关系：当 n>1 时，返回 $\frac{x}{n+f(x,n-1)}$。

2、数据类型选择

避免精度丢失，需使用 double 类型存储输入与计算结果。

3、输出格式控制

利用 printf("%.2lf", …) 控制小数点后两位，符合题目输出要求。

常见易错点：

1、递归边界遗漏

若未正确设置 if(n==1) 的返回条件，递归会陷入死循环。

建议：在写递归函数前，先推导数学公式的最底层情况。

2、整数与小数混用

若写成 1+x 而非 1.0+x，可能导致整型参与运算，精度不足。

建议：统一使用 double 类型，并在常数中加小数点。

3、输出精度错误

直接用 cout 默认可能输出多位或少位小数，不符合题意。

建议：使用 printf("%.2lf", …) 或 cout<<fixed<<setprecision(2)。

4、递归效率担忧

虽然本题数据规模不大，但递归层数过深会影响效率。

建议：理解递归原理后，也可尝试用循环迭代实现，增强灵活性。

---end---

如果你觉得这篇文章对你有帮助，欢迎点赞、收藏、关注我哦！
如果有更好的方法也可以在评论区评论哦，我都会看哒~

我们下集见~