深圳网站制作哪家便宜wordpress dopt函数
目录
一、前言
二、基本思想
三、 排序实现
1. 绝对映射
2. 相对映射
四、特性总结
五、总结
一、前言
对于之前的排序:直接插入排序、希尔排序、简单选择排序、堆排序、冒泡排序、快速排序、归并排序这些排序,都是通过比较来排序的,所以这些是比较排序。
当然还有非比较排序:计数排序、基数排序、桶排序。其中,基数排序、桶排序都不怎么常常应用,最常用的还是计数排序。本文要介绍的便是计数排序。计数排序由两种方法:绝对映射和相对映射。
二、基本思想
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
计数排序是通过开辟计数数组,统计要排序各个数据的数目,然后遍历计数数组,再从小到大将数据按计数数组的个数赋值回原数组中去。 从而完成排序。
三、 排序实现
对于一组数据,开辟的计数数组后,按照数组下标来统计原数据数据个数。如果原数据的大小对应的就是计数数组的下标,这就是绝对映射。如果原数据的最小值对应的是计数数组的第一个下标,这就是相对映射。而我们如果要用计数排序,用的也只有相对映射
1. 绝对映射
待排序的数据大小一 一对应计数数组的下标大小。
以排序数据:2,3,6,5,5,4,4,2,2,3 为例,如图所示:
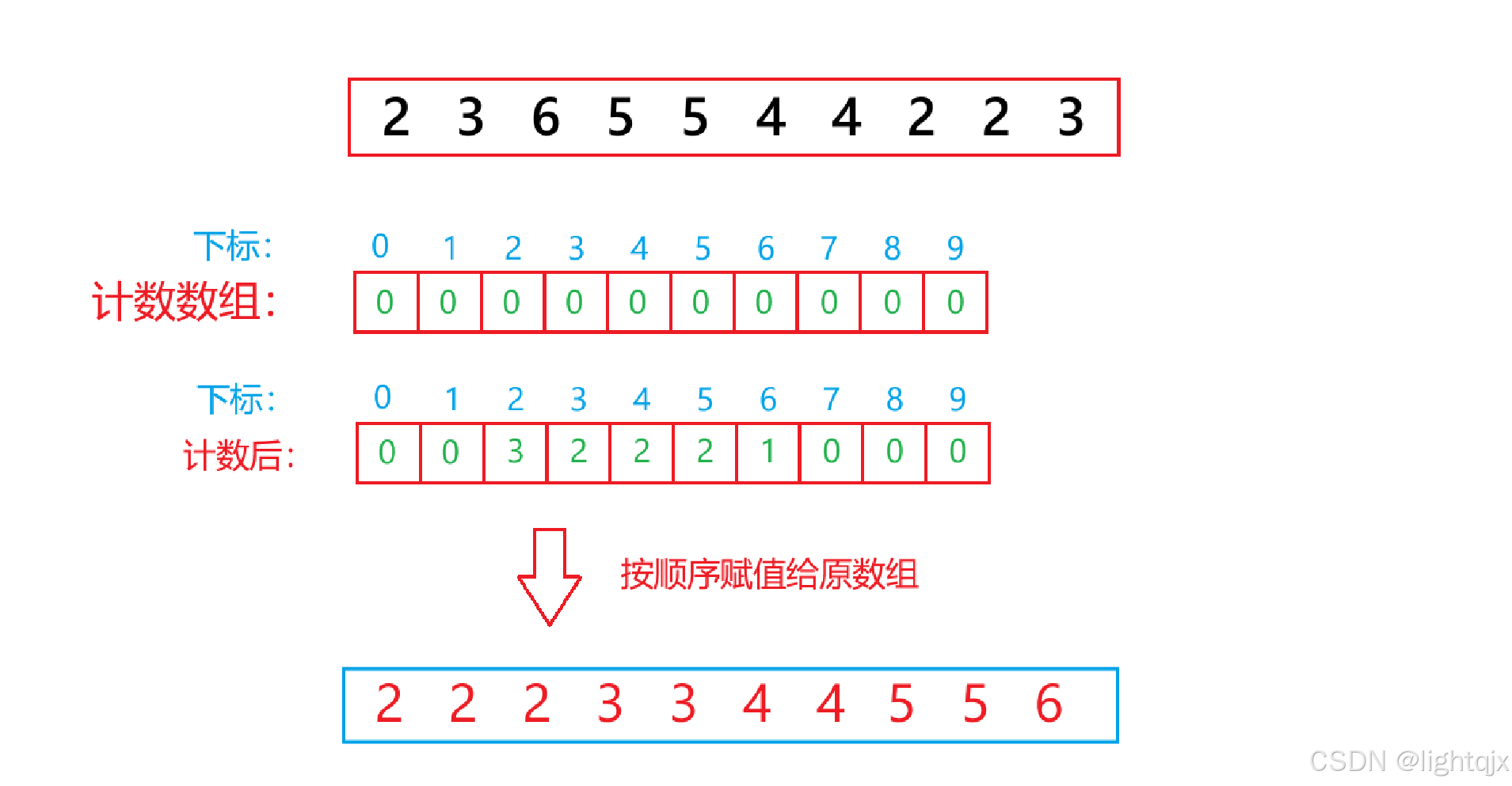
代码实现:
// 计数排序
void CountSort(int* a, int n)
{// 1.统计每个数据出现的数据//绝对映射int* countA = (int*)malloc(sizeof(int) * n);//计数数组if (countA == NULL){perror("malloc fail\n");return;}memset(countA, 0, sizeof(int) * n);// 2.计数for (int i = 0; i < n; i++){countA[a[i]]++;}// 3.排序:赋值回原数组int j = 0;for (int i = 0; i < n; i++){while (countA[i]--){a[j++] = i;}}free(countA);
}这种方法有很大的局限性,它适用于数据大小范围小的,并且数据集中的情况。
缺点:
- 如果当排序的数据是负数时,这时计数数组的下标就不能与数据对应了。
- 如果要排序的数据大小都在一个非常大的一个区间中,那么此时,计数数组开辟的空间就会造成很大的浪费了。比如:如果要排序的数据大小处于[a,b]区间,而计数数组开辟了一个可以存储b的数据的空间,那么,这里就有[0,a-1]区间的空间被浪费了。
下面的相对映射就可以解决这个问题。
2. 相对映射
相对映射并不是绝对映射那样,待排序的数据大小一 一对应计数数组的下标大小的,而是将计数数组的第一个下标位置与待排序数据的最小值进行对应。
以排序数据:6,4,5,5,7,7,8,5,5,8为例,如图所示:
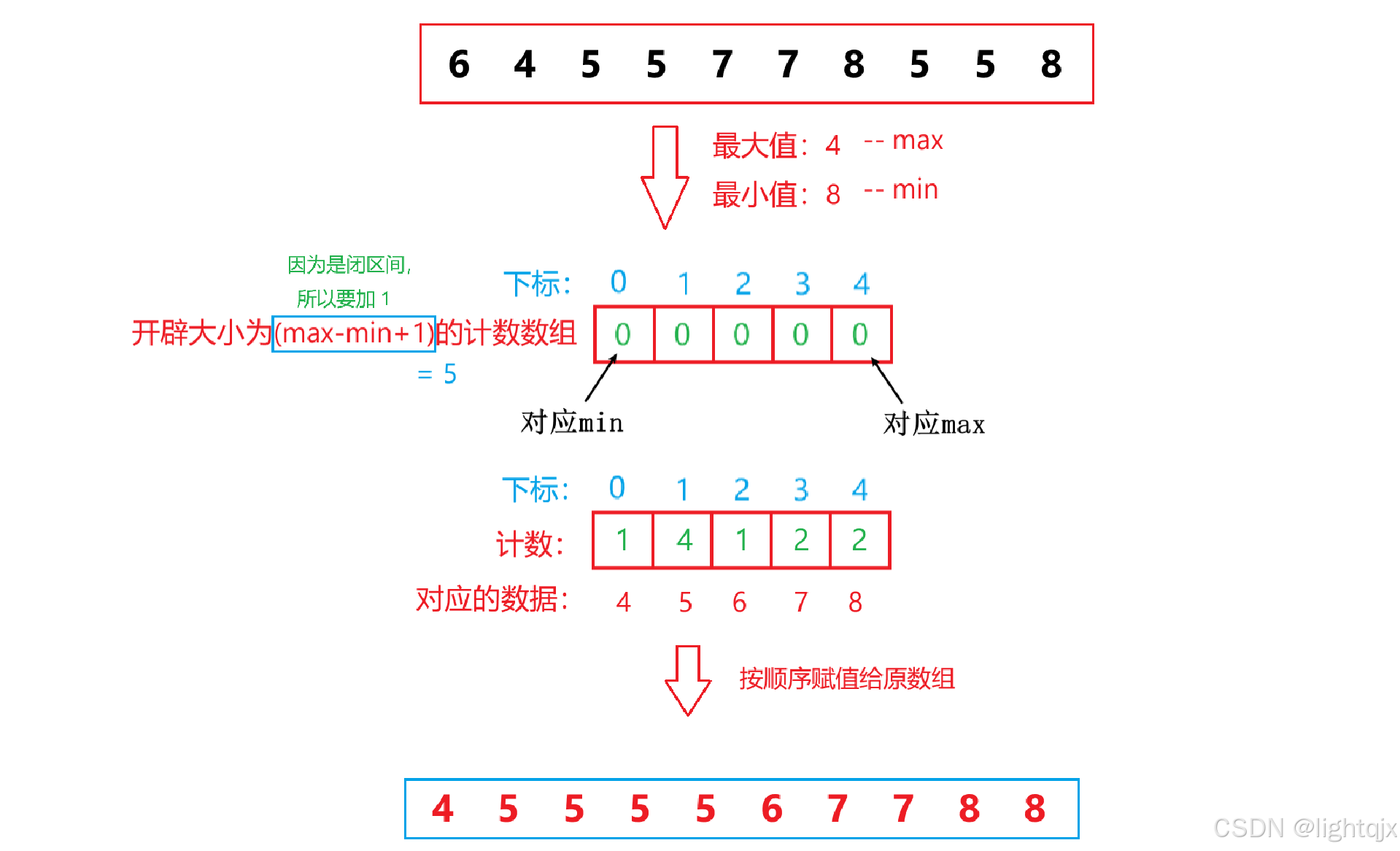
代码实现:
// 计数排序
void CountSort(int* a, int n)
{//1.统计每个数据出现的数据//相对映射int max = a[0], min = a[0];for (int i = 1; i < n; ++i){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;//统计范围int* countA = (int*)malloc(sizeof(int) * range);//计数数组if (countA == NULL){perror("malloc fail\n");return;}memset(countA, 0, sizeof(int) * range);//2.计数for (int i = 0; i < n; i++){countA[a[i] - min]++;}//3.排序:赋值回原数组int j = 0;for (int i = 0; i < range; i++){while (countA[i]--){a[j++] = i + min;}}free(countA);
}
相对映射的计数排序就是我们正真意义上的常用的计数排序。
四、特性总结
计数排序的特性总结:
- 适用情况:计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围)),与具体数据范围有关
- 空间复杂度:O(范围)
- 稳定性:稳定
五、总结
- 计数排序是一种非比较排序算法,通过统计元素出现次数进行排序。包含两种映射方式:绝对映射(直接对应元素值)和 相对映射(基于最小值偏移),指出后者更实用。
- 相对映射通过计算数据范围(range)来优化空间使用,解决了绝对映射的空间浪费问题。该算法时间复杂度为O(N+range),空间复杂度O(range),在数据范围集中时效率高且稳定,但适用范围有限。计数排序适合处理数值范围较小且集中的数据集。
感谢各位观看!希望能多多支持!
