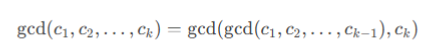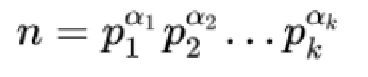当前位置：首页 > news >正文

GESP 五级（高精度+初等数论）

news 2025/10/2 15:02:57

高精度计算：

int 类型的范围为：-2147483648 到 2147483647
long long 类型的范围：-9,223,372,036,854,775,808 到 9,223,372,036,854,775,807
要计算位数比它们大的数据时，以上两种方法都计算不了，所以这里引入高精度计算。

使用数组的方式去模拟加法减法乘法除法计算

高精度加法：

使用数组的方式去模拟两个数相加的过程，最后输出结果

首先要输入两串数字
因为数字长度不一样，所以我们用两个数组逆过来存储数字
随后需要获取两个数据的最大长度，用来后面计算的遍历
最后从个位数开始计算，当个位数的值>10的时候需要进位，进位的数据可以用一个变量num存储起来，用来保存这个数。
再创建一个数组，随后将计算的结果放到对应的数组位置上去，个位就放到各位上
最后由于数组长度会大于结果的长度
所以需要去点前置0
然后再逆序输出数据，即为结果

相应程序：

const int Max_num=100;//最大长度 
string Superlong_Sums(string s1,string s2){//创建两个数组存储数据，在创建一个数组存储结果//数组长度要大于数据长度，有可能需要进一位 int arr1[Max_num+5]={};int arr2[Max_num+5]={};int arr3[Max_num+5]={};  //逆序存储数据for(int i=s1.size()-1,j=0;i>=0;i--,j++) arr1[j]=s1[i]-'0'; for(int i=s2.size()-1,j=0;i>=0;i--,j++) arr2[j]=s2[i]-'0'; //创建进位数据int num=0;//获取最长数据的长度用来遍历int maxL=max(s1.size(),s2.size());//开始计算for(int i=0;i<maxL;i++){num+=arr1[i]+arr2[i];//获取相加的结果 arr3[i]=num%10;//存储数据 num/=10;//更新进位 } //如果num!=0,说明还要进位一次if(num) arr3[maxL]=num;//逆序保存输出结果，需要去掉前置0string s="";//用来保存结果bool b=false;//用来表示有没有去掉前置0for(int i=maxL+3;i>=0;i--){if(arr3[i]==0&&!b) continue;//前置0直接跳过if(arr3[i]!=0) b=true;s+=char('0'+arr3[i]); } return s;
}

高精度减法：

使用数组进行模拟，由于减法需要借位，所以用小的数减大的数时不好操作

假设我输入两个数：求第一个数 - 第二个数
我们可以提前判断结果是正数还是负数，如果是正数说明第一个数大于第二个数
如果是负数，第二个数大于第一个数，可以用第二个数 - 第一个数最后加 - 号即可
第一步找出两数中的大数判断结果是正还是负然后使用大数-小数
计算的时候如果数据不够，往前面借一位 arr[i+1]-1; arr[i]+=10 然后再进行计算
计算完毕后要去掉前置0 如果是负数要加上 - 号

相应程序：

const int Max_num=100;//最大长度 
string Superlong_Subtracts(string s1,string s2){if(s1==s2) return "0";//如果相等直接返回 0//开始找两个数中的大值，判断结果是正还是负bool b=false;//false==正数  true=负数if(s2.size()>s1.size()||s2.size()==s1.size()&&s2>s1){//说明s2>s1 结果为负数b=true;//交换两个数的值 统一用  s1-s2计算swap(s1,s2); }//创建数据存储结果int arr1[Max_num+5]={}; int arr2[Max_num+5]={}; int arr3[Max_num+5]={}; //逆序存储数据for(int i=s1.size()-1,j=0;i>=0;i--,j++) arr1[j]=s1[i]-'0'; for(int i=s2.size()-1,j=0;i>=0;i--,j++) arr2[j]=s2[i]-'0';  //获取最长数据的长度用来遍历int maxL=max(s1.size(),s2.size());//开始计算for(int i=0;i<maxL;i++){if(arr1[i]<arr2[i]){//借位 arr1[i]+=10;//数据+10 arr1[i+1]--; }arr3[i]=arr1[i]-arr2[i];//存入数据 } //计算完存储数据，去掉前置0，判断需不需要添加 -号string s="";if(b) s+='-';//逆序保存输出结果，需要去掉前置0bool b1=false;//用来表示有没有去掉前置0for(int i=maxL+3;i>=0;i--){if(arr3[i]==0&&!b1) continue;//前置0直接跳过if(arr3[i]!=0) b1=true;s+=char('0'+arr3[i]); } return s;
}

高精度乘法：

首先乘法的计算会比较复杂一点，需要判断两位数相乘的结果属于哪个位数

首先创建两个数组存放需要计算的数，再创建一个数组存放结果
选中一个数组去乘另一个数组（默认第一个*第二个）
假设输入的数有符号，需要先处理符号，判断需要需要加上 - 号
然后根据存放数据的位置关系 index =index1+index2 存放到合适的位置上去
计算完后：每个位置上的数据还需要进行进位的处理假设个位为12 需要进行进位
使用 num+=arr3[i] arr3[i]=num%10; num/=10; 进行进位
最后去掉前置0 看是否需要加上符号
最后返回结果

相应程序：

const int Max_num=100;//最大长度 
string Superlong_Multiplication(string s1,string s2){//判断是否有符号bool b1=false;bool b2=false;int n1=0,n2=0;//数组的终点 if(s1[0]=='-') {b1=true;n1=1;} if(s2[0]=='-') {b2=true;n2=1;}//创建数据存储结果int arr1[Max_num+5]={}; int arr2[Max_num+5]={}; int arr3[2*Max_num+5]={}; //存储结果的数组长度要2倍 //逆序存储数据for(int i=s1.size()-1,j=0;i>=n1;i--,j++) arr1[j]=s1[i]-'0'; for(int i=s2.size()-1,j=0;i>=n2;i--,j++) arr2[j]=s2[i]-'0'; //开始计算for(int i=0;i<s1.size();i++){for(int j=0;j<s2.size();j++){arr3[i+j]+=arr1[i]*arr2[j];//累计数据 }} //开始进位int maxL=s1.size()+s2.size()-1; int num=0; for(int i=0;i<=maxL;i++){num+=arr3[i];arr3[i]=num%10;num/=10; }if(num) arr3[maxL]=num;//进位//开始获取结果string s="";if(b1^b2) s+='-';//如果满足异或说明为负数//逆序保存输出结果，需要去掉前置0bool b3=false;//用来表示有没有去掉前置0for(int i=maxL+3;i>=0;i--){if(arr3[i]==0&&!b3) continue;//前置0直接跳过if(arr3[i]!=0) b3=true;s+=char('0'+arr3[i]); } return s;  
}

高精度除法：

首先要输入两个数： A B (都为正数)
如果A的长度<B的长度|| A的长==B的长度&&A<B 说明A<B 直接返回 0
首先创建一个字符串s遍历A，如果s<B 直接加上A[i]
当s>B的时候说明可以进行除法运算了，我们使用高精度减法模拟除法运算
使用 num来统计商当s>B 时 s - B;num++;直到s<B退出，保存num这个结果
如果s=="0" 说明刚好能整除我们要去掉前置0 所以要把s设置为空
当 s=="" A[i]=='0'的时候直接把A[i]添加到结果后面

特殊情况处理：

相应程序：

string Superlong_Subtract(string s1,string s2){ //高精度减法   //创建数据存储结果int arr1[Max_num+5]={}; int arr2[Max_num+5]={}; int arr3[Max_num+5]={}; //逆序存储数据for(int i=s1.size()-1,j=0;i>=0;i--,j++) arr1[j]=s1[i]-'0'; for(int i=s2.size()-1,j=0;i>=0;i--,j++) arr2[j]=s2[i]-'0';  //获取最长数据的长度用来遍历int maxL=max(s1.size(),s2.size());//开始计算for(int i=0;i<maxL;i++){if(arr1[i]<arr2[i]){//借位 arr1[i]+=10;//数据+10 arr1[i+1]--; }arr3[i]=arr1[i]-arr2[i];//存入数据 } //计算完存储数据，去掉前置0，判断需不需要添加 -号string s="";//逆序保存输出结果，需要去掉前置0bool b1=false;//用来表示有没有去掉前置0for(int i=maxL+3;i>=0;i--){if(arr3[i]==0&&!b1) continue;//前置0直接跳过if(arr3[i]!=0) b1=true;s+=char('0'+arr3[i]); } return s;
}string Text(string s1,string s2,int &num){//计算结果  string s=s1;num=0;while(s.size()>s2.size()||s.size()==s2.size()&&s>=s2){s=Superlong_Subtracts(s,s2);cout<<"s="<<s<<endl; num++;} return s;//返回计算过的值，num保存了减的次数 
} 
string Superlong_Division(string s1,string s2){ //高精度除法//如果被除数小于除数if(s1.size()<s2.size()||s1.size()==s2.size()&&s1<s2) return "0";//直接返回0 //开始进行计算 借助减法进行运算string s="";//模拟运算过程 string str="";//用来保存运算结果for(int i=0;i<s1.size();i++){if(s==""&&s1[i]=='0') str+=s1[i]; //当500/5 时  str为空 但后面有两个0 需要直接统计=100else s+=s1[i]; if(s.size()>s2.size()||s.size()==s2.size()&&s>=s2){ //比被除数大 开始统计 int number=0;s=Text(s,s2,number);//进行计算 cout<<"number="<<number<<endl; str+=to_string(number);if(s=="0") s="";//如果刚好能整除为0 要置为空不然就形成前缀0 }}cout<<"s="<<s<<endl;//余数 return str;//返回商 
}int main(){string s1,s2;cin>>s1>>s2;cout<<Superlong_Division(s1,s2);return 0;
}

初等数论：

素数和合数：

素数：又称质数，是指在大于1的自然数中，除了1和它本身以外不再有其他因数
合数：除了1和其本身外还有其他正因数的大于1的正整数，
规定1既不是质数也不是合数
合数都是由质数相乘得来的，所有合数都可以分解成小于它本省的质数相乘的形式表示
所以合数可以分解成多个质因数相乘

找素数

暴力解法：

直接遍历2 — n的范围的数判断是否满足除了一和它本身外没有数能整除

//判断是否为质数 
bool Prime_number(int n){for(int j=2;j<i;j++){if(i%j==0) return false;//有其他因数返回假 } return true;
}//统计范围素数个数
int find_number_Prime(int n,int m){ //n和m的为范围 n>=2 m<10e9//暴力解法int num=0;//统计个数 for(int i=n;i<=m;i++){//判断是否为质数if(Prime_number(i)) num++;} return num;
}

暴力优化：

由于除2外的偶数都不是质数，所以我们可以排除偶数，只计算奇数
而且当数>num/2 时相除的结果为1.几，为小数，可以不用判断这部分因数
所有有两个优化的空间

//判断是否为质数 
bool Prime_number(int n){for(int j=2;j<i/2;j++){ //优化1：因数判断的范围 if(i%j==0) return false; } return true;
}
//统计范围素数个数
int find_number_Prime(int n,int m){ //n和m的为范围 n>=2 m<10e9//暴力解法int num=0;//统计个数 int n1=n;if(n1==2){ //特殊处理2这个值 num++;n1++;} for(int i=n1;i<=m;i+=2){ //优化2使用奇数进行判断 //判断是否为质数if(Prime_number(i)) num++;} return num;
}

埃氏筛法：

将已经筛选出的质数的倍数全部剔除，即可留下质数

由于合数都是其小于本身的质数倍数
当判断到质数是，将（范围内）的倍数都可以排除掉
需要创建一个 bool 类型数组判断它是否被剔除

埃氏筛法模板：

//埃氏筛法模板
const int num=10001;
int data[num]={};//数组存储数据
bool N[num]={false};//用来标记是不是素数 
int k=0;//用来存储素数的位置 
void find_prime_number1(int n)
{N[1]=true;//1不是素数for(int i=2;i<=n;i++){if(!N[i]){data[++k]=i;//是素数 存储数据for(int j=2*i;j<=N;j+=i) N[i]=true;//把i的倍数都剔除} } 
} 
//时间复杂度：0(nlogn)   空间复杂度 O(N)

埃氏筛法解题：

//埃氏筛法 统计素数个数 
int find_number_Prime(int n,int m){int num=0;//统计个数 bool  b[m+10]={false};//判断是否被剔除b[0]=b[1]=true;//0 1 不是素数//从2开始剔除 for(int i=2;i<=m;i++){if(!b[i]){for(int j=2*i;j<=m;j+=i)b[j]=true;//将倍数剔除 }} //剔除完后统计个数for(int i=n;i<=m;i++){if(!b[i]) num++;} return num;
}

线性筛法：

埃氏筛法剔除时会剔除掉重复的数据所以还可以进行优化

让每个数都被其最小的质因数筛掉合数=最小质因子*其他数（可以是任意数）
创建一个动态数组存储已经赛选得到的质数
剔除 i和已有质数的倍数
遍历已有质数prime[i] 当 I*prime[i]>max时退出 else 进行合数的标记
当 i%prime[i]==0；时代表i可以整除这个质数时你在往下遍历时就不是最小的质因子了，所以也要退出

线性筛法模板：

const int Num=10001;
int da[Num]={};//存储数组 
int p=0;
bool M[Num]={false};//用来标记是否为素数 
void find_prime_number2(int n)
{M[1]=true;//1不是素数for(int i=2;i<=n;i++){if(!M[i]) da[++k]=i;//如果是素数，存储数据for(int j=1;i*da[j]<=n;j++)//开始筛数 {M[i*data[j]]==true;//筛除该数if(i%data[j]==0) break;//当i能够整除data[j]时退出 } } 
}
//时间复杂度 O(n)  空间复杂度O(n)

线性筛法解题：

//线性筛法 统计素数个数 
int find_number_Prime(int n,int m){int num=0;//统计个数 bool  b[m]={false};//判断是否被剔除b[0]=b[1]=true;//0 1 不是素数vector<int> v1;//存储质数 //从2开始剔除 for(int i=2;i<=m;i++){if(!b[i]) v1.push_back(i);//添加进数组for(auto p:v1){//遍历v1if(i*p>m) break;b[i*p]=true;//筛除该数if(i%p==0) break; }} //剔除完后统计个数for(int i=n;i<=m;i++){if(!b[i]) num++;} return num;
}

数字选取:

题目分析：

题目的意思是：找1-n中最长互质的数

质数：肯定是符合条件的
合数：合数是由一个或多个质数相乘得来的，所以可能会影响多个数据，使用了合数及代表使用不了相乘的质数
所以这道题的意思是求1-n中质数的个数（1不是质数但要加上）
这题主要考的的阅读理解

线性筛法解题：

#include<iostream>
#include<vector>
using namespace std;
vector<int> v1;
bool b[100005];//代表是否被访问 int main(){//由于一个合数=1个或多个质数的积//所以取一个合数，还不如取相应的质数//所以求范围内的质数个数//使用线性筛法 int n; cin>>n;for(int i=2;i<=n;i++){if(!b[i]) v1.push_back(i);for(int p:v1){if(i*p>n) break;b[i*p]=true;if(i%p==0) break;}}cout<<v1.size()+1; return 0;
}

因数和倍数：

因数：因数又称约数，某个整数除以a时没有余数
倍数：一个整数能够被另一个整数整除，这个整数就是另一整数的倍数，一个数的倍数有无数个，也就是说一个数的倍数的集合为无限集

找因数：

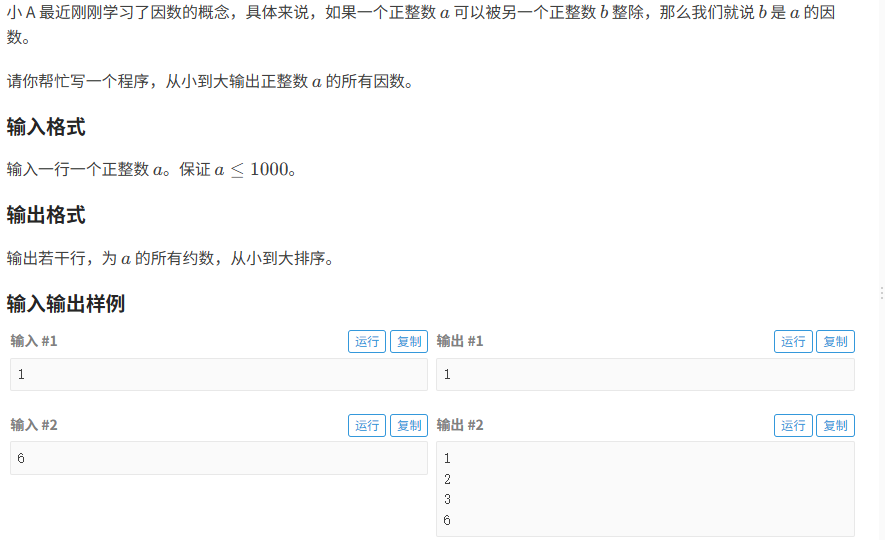
求a的所有因数：

首先最小的因数肯定是 1
最大的因数为a它本身
由于因数能被a整除，所以判断是否有余数即可
从小到大排序，我们从小到大遍历即可

相应程序：

#include<iostream>
using namespace std;
int main()
{int a;cin>>a;for(int i=1;i<=a;i++) if(a%i==0) cout<<i<<endl;return 0;
}

奇偶性判断：

奇数：当一个数除2有余数的时候就是奇数（不是2的整数倍数）

偶数：当一个数除以2没有余数的时候就是偶数（是2的整数倍数）

代码实现形式：

奇数： n%2==1
偶数： n%2==0

奇偶判断：

void odd_even_number(int n){ //奇偶性判断 if(n%2==0) cout<<"偶数"<<endl;else cout<<"奇数"<<endl; 
}

奇数和偶数

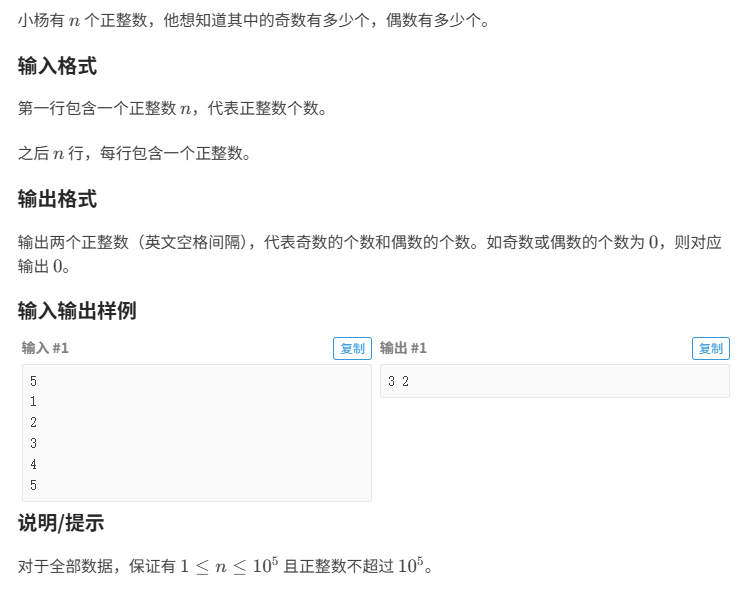
相应程序：


#include<bits/stdc++.h>
using namespace std;
int a=0,b=0,n;
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>c[i];if(c[i]%2!=0)a++;else b++;}cout<<a<<" "<<b;return 0;
}

最大公因数：

最大公约数：也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个

最大公因数1：

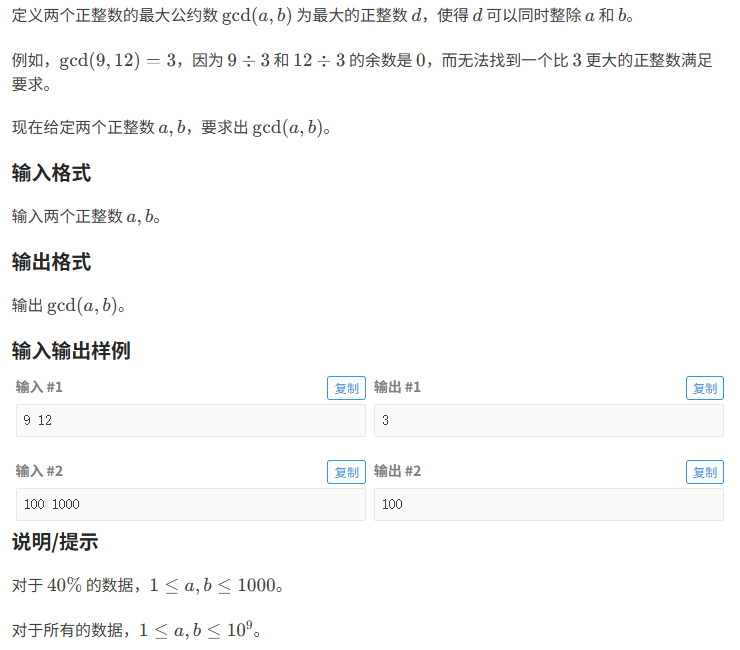
暴力求解：

最大公因数：可以被A整除也可以被B整除
大的数不可能是两者的最大公因数
小的数有可能是两者的最大公因数
它们的最小公因数为1（也有可能是最大公因数当值为 3 11都为质数是最大公因数为1）
由于找最大，我们从后往前遍历起点为 min(A,B) 终点为1
找到可以整除两个数的结果就退出循环

相应程序：

int find_MAX_factor(int A,int B){//找最大公因数 if(A==0)for(int i=min(A,B);i>=1;i--){if(A%i==0&&B%i==0){return i;//直接返回  最小为1 }} 
}

辗转相除法：

欧几里得算法：又称辗转相除法，是指用于计算两个非负整数a，b的最大的公约数。应用领域有数学和计算机两个方面。计算公式：gcd(a,b) = gcd(b,a mod b)

以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数

数学证明：

假设两个数a和b（a > b），它们的最大公约数为c，存在整数m和n，使得a = mc和b = nc。

设r为a除以b的余数，即a = kb + r，其中k是整数。

由于a和b都能被c整除，因此r也能被c整除，即r = a - kb = mc - knc = (m - kn)c。

由此可见，b和r的最大公约数也是c，即gcd(b, r) = c。

因此，可以通过不断地将除数和余数进行辗转相除，直到余数为0，最后的除数就是最大公约数。

相应程序：

//递归的实现
int gcd(int a, int b)
{if (a % b == 0)return b;else return gcd(b, a % b);
}//循环的实现
int gcd1(int a,int b){while (1){if (a % b == 0){return b;}int c = a % b;a = b;b = c;}
}

最大公因数2：

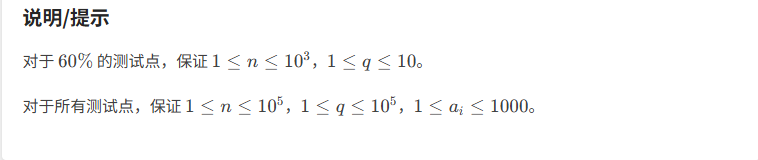
题目分析：

题目的意思是：给出n个数据给出一个m 让n个数据+1~+m

分别求 +1~+m的数据中的每组数据的公因数

首先两个相同数的公因数是相同的，所以数据可以先进行去重
由于数据最大为1000 且 m最大为10 创建 a[1020]的数组即可

然后使用辗转相除法求公因数，需要注意的是第一个数要大于第二个数
可以将数据排一下序从小到大进行处理
最后就是循环遍历：
根据这个公式进行计算即可
如果结果为1了就不需要计算了，节省时间（所以从小到大计算节约时间）

相应程序：

#include<iostream>
#include<algorithm>
using namespace std;
int a[1020];
bool b[1020];
int index=0;//数组的下标 
int n,m; 
int gcd(int a,int b){if(a<b) swap(a,b);if(b==0) return a;return gcd(b,a%b);
}
int main(){cin>>n>>m;int num;for(int i=0;i<n;i++){cin>>num;if(!b[num]) {a[index++]=num;b[num]=true;//设置为已访问 }}sort(a,a+index);//从小到大排序for(int i=1;i<=m;i++){int data=a[0]+i;for(int j=1;j<index;j++){data=gcd(data,a[j]+i);if(data==1) break; //num==直接退出 }cout<<data<<endl; } return 0;
}

最小公倍数：

两个或多个整数公有的倍数叫做它们的公倍数

同时可以整数所有数
且这个数是最小的

求最小公倍数

求A和B的最小公倍数最小公倍数再int 范围内（学习思路，就不用高精度了）

暴力解法：

由于最小公倍数，可以整除A和B 所以 A*B肯定是两者的公倍数，但不一定是最小公倍数
所以我们可以暴力求解：遍历 1— A*B 找到第一个满足能整除 A和B的数即可

//找最小公倍数 
int find_lowest_common_multiple(int A,int B){ for(int i=1;i<=A*B;i++){if(i%A==0&&i%B==0){return i;}} 
}

暴力优化：

由于可以整除A和B，遍历的起点可以为 max(A,B) 然后累加 max(A,B)即可
这样可以节省很多计算时间

//找最小公倍数 
int find_lowest_common_multiple(int A,int B){ int num=max(A,B);for(int i=num;i<=A*B;i+=num){if(i%A==0&&i%B==0){return i;}} 
}

公式法：

最小公倍数=两数相乘/最大公因数

//找最大公因数 
int gcd(int a.int b){if(a<b) swap(a,b);if(b==0) return a;else{return gcd(b,a%b);}
} //找最小公倍数
int find_lowest_common_multiple(int A,int B){ return A*B/gcd(A,B);
}

唯一分解定理：

任何一个大于1的整数n都可以分解成若干个素因数的连乘积，如果不计各个素因数的顺序，那么这种分解是惟一的。

质数：只与1和本身能整除
合数：是由质数相乘得来的
质数可以分解为本身
合数可以分解为：质数*质数......

所以说，每当一个大于1的自然数，要么是质数，要么就可以写成两个或多个的质数的乘积，由于质数是唯一的，所以这些质因子的排列也是唯一的。

n=p1*p2*…*pm，其中p1≤p2≤…≤pm皆素数，上式常简记为

质因数分解1：

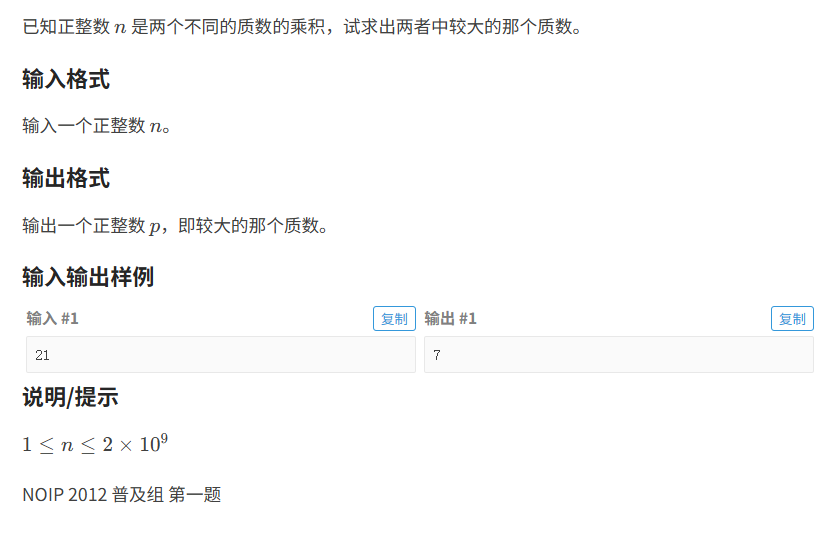
题目分析：

n是两个不同质因数的乘积，求出较大的那个质数

由于质数具有唯一性
所以从头遍历，找到第一个质数然后输出 n/num 即为最大质数

相应程序：

#include<iostream>
#include<iomanip>
using namespace std;
int main()
{int n;cin>>n;for(int i=2;i<=n;i++){if(n%i==0){cout<<n/i;break;}} return 0;
}

质因子分解2：

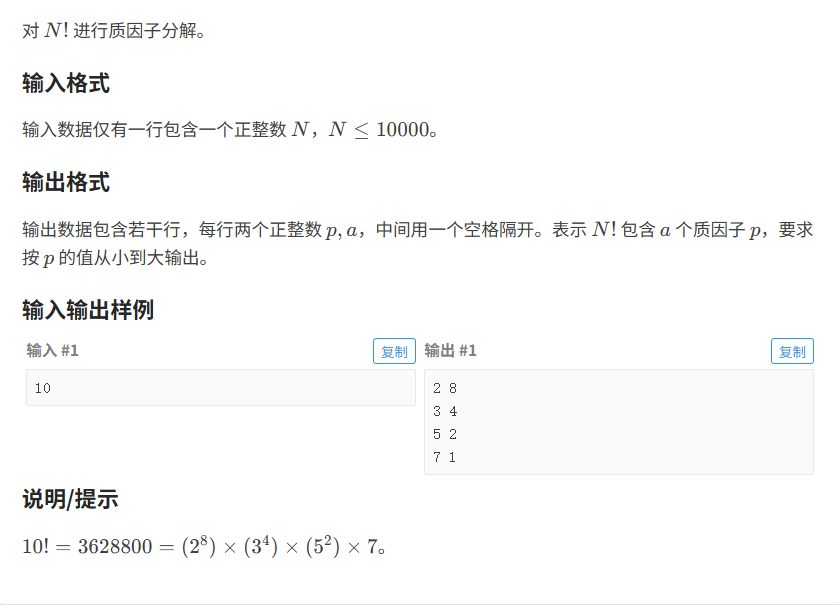
题目分析：

就是给出一个阶乘：将这个阶乘分解成质因子+指数的形式表示由于N是小于10000的

可以使用桶来装这些因子个数
然后对1-n的数进行分解即可

相应程序：

#include<iostream>
#include<vector> 
using namespace std;
int arr[10005]={0};//桶装因子个数
int n;
int max_num=-1;//保存最大因子 void text(int num){ //分解数for(int i=2;i<num;i++){if(num%i==0){if(i>max_num) max_num=i; int num1=0;while(num%i==0){num/=i;num1++;}arr[i]+=num1;}}if(num>1) {if(num>max_num) max_num=num;arr[num]++;}
}
int main(){cin>>n;for(int i=2;i<=n;i++){text(i);} for(int i=2;i<=max_num;i++){ //输出因子及其个数if(arr[i]!=0){cout<<i<<" "<<arr[i]<<endl; }}return 0;
}

质因数分解3：

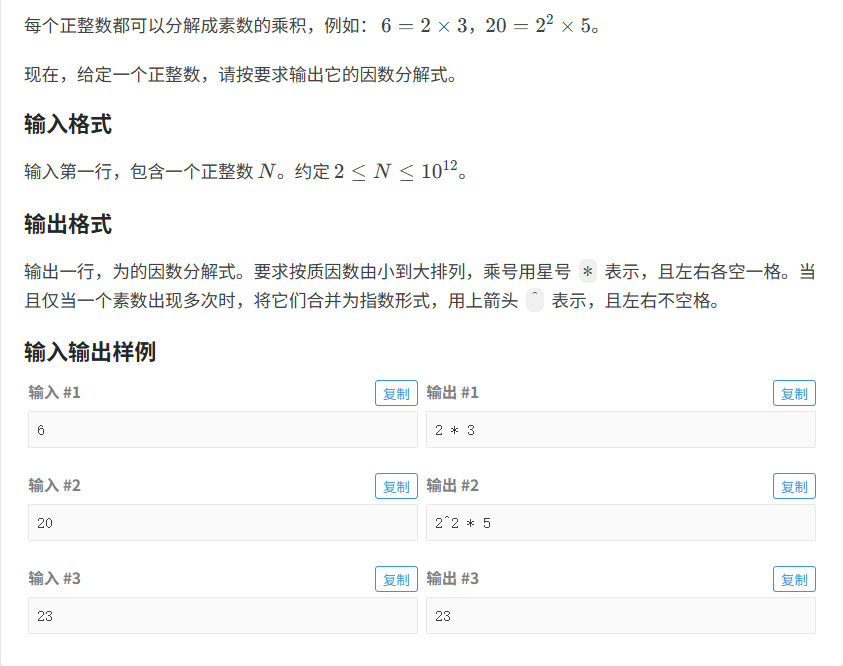
题目分析：

题目的意思是让我们对一个数进行拆分，分别以因素及其指数的形式表示

第一步要统计因数及其个数，可以创建一个结构体
最小的质因数为2，可以从2开始遍历分解
如果n%2==0 说明可以整除需要统计这个因数的个数 n/=2；
否则进入下一个因数，由于剔除了前面的因数所以间接性的把这个因数的最小质因子的数给排除了，所以直接访问后面的数即可
如果除到最后还是大于1，说明是质数，直接添加它本身

相应程序：

#include<iostream>
#include<vector>
using namespace std;
struct number{long long x,cnt;
};vector<number> data;//存储因子及其个数
void get_data(long long n){for(long long i=2;i<n/i;i++){ //遍历数据int num=0;if(n%i==0){//如果可以整数while(n%i==0){//除到不能整数为止n/=i;num++;	//统计个数}data.push_back({i,num});//添加数据 }}//如果还>1 把这个数据添加if(n>1) data.push_back({n,1}); 
}
int main(){long long n;cin>>n;get_data(n);for(int i=0;i<data.size();i++){if(i>0&&i<data.size()) cout<<" * ";if(data[i].cnt==1) cout<<data[i].x;else{cout<<data[i].x<<"^"<<data[i].cnt;}} return 0;
}

B-smooth 数

题目分析：

题目的意思是求1-n之间最大质因数小于等于B的数的个数

1 不是质数但结果为空集所以也算

埃氏+线性解题：

使用线性筛法将范围内所有质数找出来
找出第一个大于B的质数
使用埃氏筛法筛除所有大于B的质数的倍数
最后统计没有被筛除的数据

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int n,B; 
vector<int> v1; 
bool b[1000005];//线性筛法标记
bool b1[1000005];//埃氏筛法标记 
int number=0;//统计个数 
int main(){cin>>n>>B;//使用线性筛法先找出范围内所有质因子b[0]=b[1]=true;for(int i=2;i<=n;i++){if(!b[i]) v1.push_back(i);for(auto p:v1){if(p*i>n) break;b[p*i]=true;if(i%p==0) break; }} //找到第一个大于等于B的质数位置 auto index=upper_bound(v1.begin(),v1.end(),B);int num=*index;//获取第一个大于B的质数 //埃氏筛法开始剔除 for(;index!=v1.end();index++){for(int i=1;i*(*index)<=n;i++){b1[i*(*index)]=true;}}for(int i=1;i<=n;i++){ //统计个数if(!b1[i]) number++;	}cout<<number;return 0;
}

埃氏筛法解题：

埃氏筛法：将质数的倍数进行剔除

这里可以再进阶一下，我们可以保留这个质数因子到这个被剔除数据的位置中

当数为6 时，它同时会被2 3这两个质数整除当被2剔除时保存2 被3整除时保存3
刚好可以保存到这个数的最大质因子
最后统计范围内<B的质因子即可

#include<bits/stdc++.h>
using namespace std;int a[1000005];//保存最大质因子数组
int number=0;
int main(){int n,b;cin>>n>>b;for(int i=2;i<=n;i++){ //埃氏筛法if(!a[i]){ //当是质数时for(int j=i;j<=n;j+=i){//将倍数保存这个质因子a[j]=i;}}}for(int i=1;i<=n;i++){//统计<=b的数据if(a[i]<=b) number++;}cout<<number;return 0;
}

小杨的幸运数字：

题目分析：

题目的意思是：判断一个数是不是刚好被两个不同的质数相乘

暴力解法很容易超时
使用线性筛法+暴力：先将所有的质数先求出来，然后再一个一个乘进行判断
使用埃氏筛法：统计被质数抹除的次数即可

埃氏筛法解题：

当使用埃氏筛法时：如果一个数是多个质数的积时，每当执行到质数时都会将其抹除一次，所以抹除的时候可以统计次数

例如 30=2*3*5 它会被 2 3 5 各抹除一次，统计次数即为质因子个数

#include<iostream>
using namespace std;const int max_number=1e6;//最大数 
int b[max_number+5];//判断是否为幸运数 
int n;
int main(){cin>>n;//使用埃氏筛法进行剔除数据for(int i=2;i<=max_number;i++){if(!b[i]){for(int j=2;j*i<=max_number;j++){b[i*j]++;//抹除的次数+1 }} } int num;for(int i=1;i<=n;i++){cin>>num;if(b[num]==2) cout<<1<<endl;else cout<<0<<endl;}return 0;
}

约数个数定理：

对于一个大于1正整数n可以分解质因数：

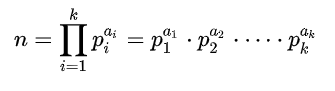
则n的正约数的个数就是：

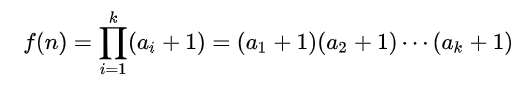
其中a1、a2、a3…ak是p1、p2、p3，…pk的指数。

约数和定理：

对于一个大于1正整数n可以分解质因数：n=p1a1*p2a2p3^a3…*pk^ak,
则由约数个数定理可知n的正约数有(a₁+1)(a₂+1)(a₃+1)…(ak+1)个，
那么n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个正约数的和为 f(n)=(p10+p11+p12+…p1a1)(p20+p21+p22+…p2a2)…(pk0+pk1+pk2+…pkak）

定理证明：