0.1 tensorflow例1-梯度下降法

例1：求函数y= (x^2-9)^2的极值位置，即求其导数为0的值y'=4*x*(x^2-9)。

定义loss = y'^2. 其极值位置在x轴-3，0，3位置。

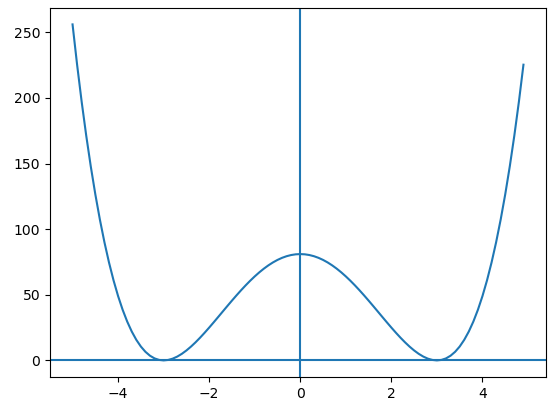
代码如下，效果良好，从5开始可以找到3的极值位置。从-5开始可以-3的极值位置；从0.5开始找到极值点0的位置。

import numpy as np
import tensorflow as tf
from matplotlib import pyplot as plt
#'求 y= (x^2-9)^2  的最小值'
#'即求梯度：y'=4*x*(x^2-9)=0的位置x = tf.Variable(tf.constant(-5,dtype=tf.float32))
lr=0.01
epoch = 1000
for step in range(epoch):with tf.GradientTape() as tape:loss = tf.square( 4*x*(x*x-9))grads = tape.gradient(loss,x)x.assign_sub(lr*grads/np.abs(grads))print("After %s epoch, x is %.2f, loss is %.2f" %(step,x.numpy(),loss))xRange = tf.range(-5,5,0.1)
x1=[]
y1=[]
y2=[]
for xpos in xRange:x1.append(xpos)y1.append( np.square (xpos*xpos - 9))y2.append( 4*xpos*(xpos*xpos - 9)       )
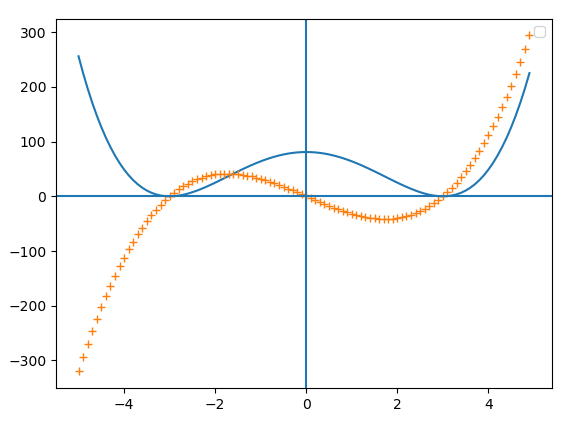
plt.plot(x1,y1,'-',x1,y2,'+')
plt.axhline()
plt.axvline()
plt.show()

下图打印了函数以及其导数的图片