笔记:标准化和归一化的学习
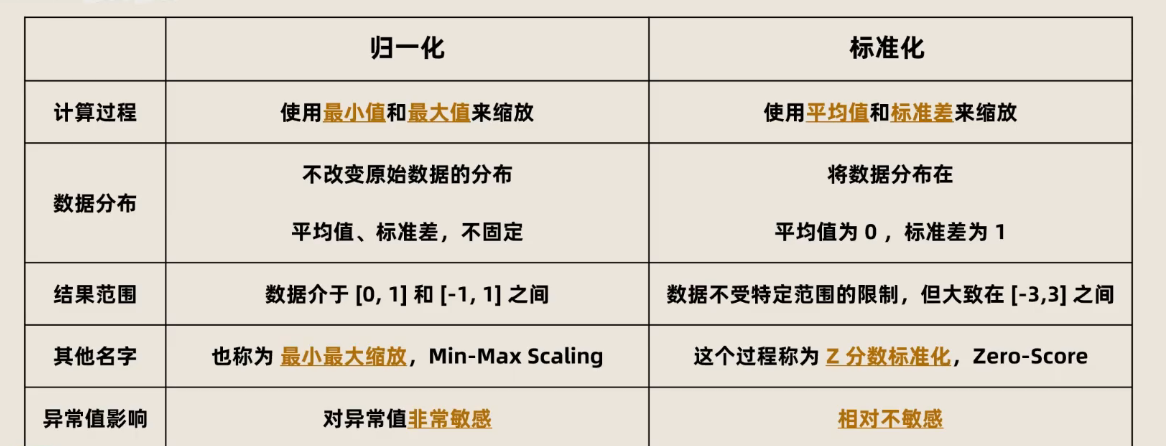
当然可以!我们用一个通俗易懂的例子来解释**标准化(Standardization)**和**归一化(Normalization)**,以及它们的**特点、区别和相同点**。
---
### 🌰 举个生活中的例子:考试成绩
假设你有两个同学:
- 小明:数学考了 90 分(满分 100)
- 小红:语文考了 180 分(满分 200)
现在你想比较他们谁“考得更好”,但因为两门课的**满分不同、分数范围不同**,直接比 90 和 180 没有意义。这时候就需要对分数做“处理”,让它们在同一个尺度上比较——这就是**特征缩放(Feature Scaling)**,而标准化和归一化就是两种常见的方法。
---
## 一、归一化(Normalization)
### ✅ 做什么?
把数据缩放到一个固定的范围,通常是 **[0, 1]**。
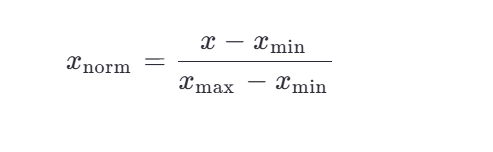
### 📌 用考试例子:
假设你有一组数学成绩:[60, 70, 80, 90, 100]
- 最小值 = 60,最大值 = 100
- 小明的 90 分归一化后:
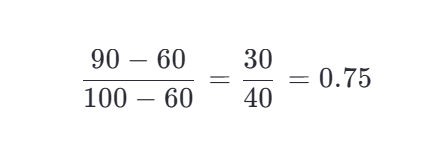
有分数都变成 0 到 1 之间的数。
### ✅ 特点:
- 保留原始数据的分布形状(只是“压缩”了范围)
- 对**异常值敏感**(如果有个同学考了 200 分,最大值变大,其他人都被“压扁”了)
- 适合数据分布**没有明显正态性**,且你知道最大最小值的情况
---
## 二、标准化(Standardization)
### ✅ 做什么?
让数据的**均值为 0,标准差为 1**,也就是转换成“标准正态分布”的形式(但不一定真的正态)。
### 📐 公式(Z-score 标准化):
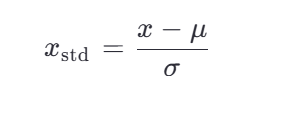
### 📌 用考试例子:
还是数学成绩:[60, 70, 80, 90, 100]
- 均值 \(\mu = 80\)
- 标准差 \(\sigma ≈ 15.81\)
- 小明的 90 分标准化后:
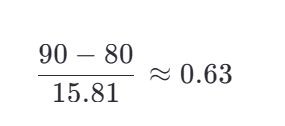
结果:数据围绕 0 上下波动,单位是“标准差”。
### ✅ 特点:
- 不限制数据范围(可能得到 -2、3 这样的值)
- 对**异常值不那么敏感**(因为用的是均值和标准差,不是极值)
- 适合数据近似**正态分布**,或用于像 SVM、逻辑回归、PCA 等对数据尺度敏感的算法
---
## 三、相同点 ✅
| 相同点 | 说明 |
|--------|------|
| 目的相同 | 都是为了**消除量纲影响**,让不同特征在相同尺度上比较 |
| 都是特征工程步骤 | 通常在机器学习建模前进行 |
| 都是线性变换 | 不改变数据的原始分布形状(比如偏斜还是偏斜) |
---
## 四、主要区别 ❗
| 对比项 | 归一化(Normalization) | 标准化(Standardization) |
|--------|--------------------------|----------------------------|
| 输出范围 | 固定,如 [0,1] 或 [-1,1] | 不固定,通常在 [-3,3] 之间(但可能更广) |
| 是否依赖极值 | 是(用最大/最小值) | 否(用均值和标准差) |
| 对异常值敏感度 | 高(一个极大值会拉垮整体) | 较低 |
| 适用场景 | 神经网络、图像像素(0~255→0~1)、KNN | 线性模型、PCA、SVM、逻辑回归等 |
| 数据分布假设 | 无特别要求 | 更适合近似正态分布的数据 |
---
## 🎯 一句话总结:
- **归一化**:把数据“压缩”到 0~1,适合你知道数据边界的情况。
- **标准化**:把数据“居中”并按波动程度缩放,适合数据有异常值或用于统计模型。
> 💡 小技巧:如果你不确定用哪个,**先试试标准化**,它在大多数机器学习场景中更稳健!
