【Leetcode高效算法】用双指针策略打破有效三角形的个数

前言：欢迎各位光临本博客，这里小编带你直接手撕**，文章并不复杂，愿诸君**耐其心性，忘却杂尘，道有所长！！！！

IF’Maxue：个人主页
 🔥 个人专栏:
《C语言》
《C++深度学习》
《Linux》
《数据结构》
《数学建模》

⛺️生活是默默的坚持，毅力是永久的享受。不破不立！

题目解析

题目链接：有效三角形的个数

咱们先来明确下问题：

• 给一个非负整数的数组，咱们要找出其中能组成三角形的三个数有多少个？

• 要是数组里有重复的元素，比如[2,2,2]，这也算一个有效的三元组

三角形的构成条件

数学里说，三个数a、b、c要组成三角形，需要满足：

即两边之和大于第三边

• 普通思路：分别判断三个边
      a + b > c
      a + c > b
      b + c > a

---

• 高效思路：
  咱们先把这三个数排个序，比如让a ≤ b ≤ c。这时候你会发现：后面两个条件不用看了，只要满足a + b > c，这三个数就能组成三角形！

---

解法一：暴力枚举法（效率较低但直观）

    
最直接的思路是：遍历数组中所有可能的三元组，逐一验证其是否能构成三角形。

具体实现：使用三重循环，通过索引i、j、k枚举所有组合，检查每组三个数是否满足三角形不等式a + b > c。

for(i = 0; i < n; i++)for(j = i + 1; j < n; j++)for(k = j + 1; k < n; k++)check(i, j, k);

需要注意的是：

• 当数组规模较大时（如n=1000），该算法的时间复杂度为O(n³)，计算量会显著增加，因此在实际应用中效率较低。

---

解法二：双指针算法（又快又巧妙）

 
既然暴力法太慢，咱们换个思路。利用数组的单调性（排序后），用双指针来加速计算。

核心思路：

1. 先给数组排个序(方便咱们用“a ≤ b ≤ c”的条件)
2. 固定最大的数c（也就是下标为n的元素）
3. 在c左边的区间里（也就是0到n-1），用两个指针left和right来找a和b，快速统计满足a + b > c的组合（对应双指针算法的图片）
   

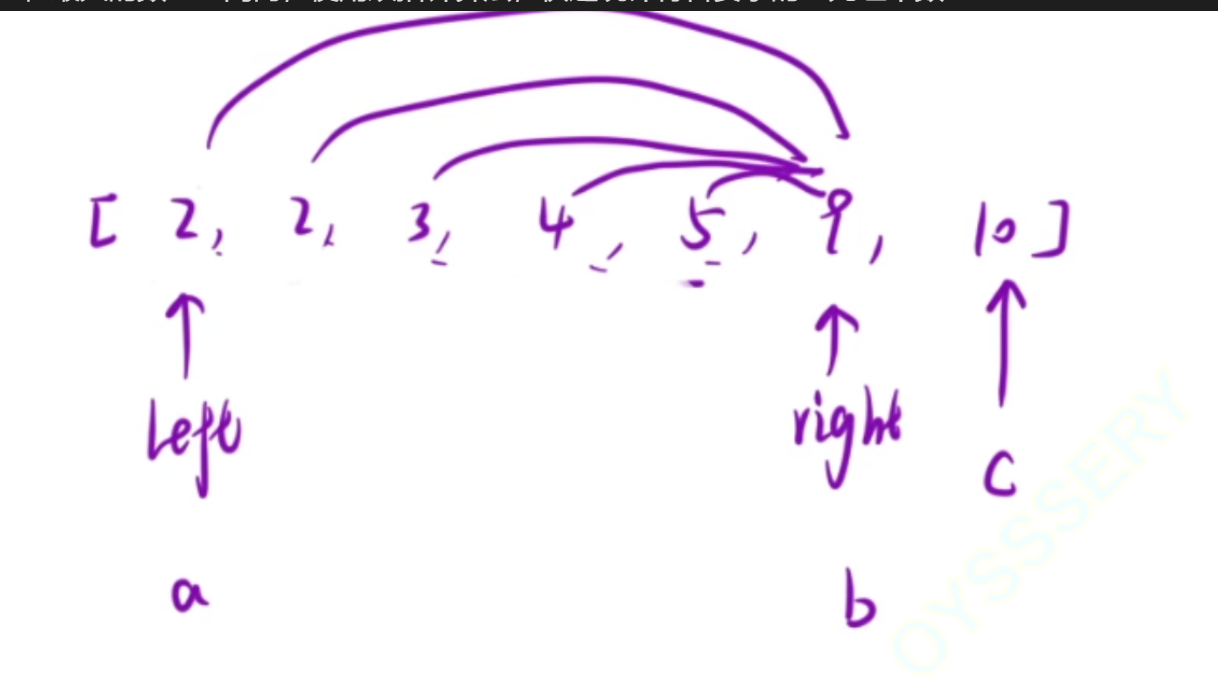
具体操作

• 首先我们知道这是一个有序数组，我们用最小的和最大的相加
  • a+b>c 那么a后面的所有数与b相加>c，所以可以与c和b构成三角形的三元组个数为：right-left
  • a+b<=c 那么说明：这里的a无法与b和c构成三角形，所以我们将a往后移。
• 这里用最大数10遍历完之后，然后用往前移动，用9当最大数。直到下标为2的时候。
  就这么一步步，把每个可能的最大数c都试一遍，直到n=2（因为至少要三个数才能组成三角形）。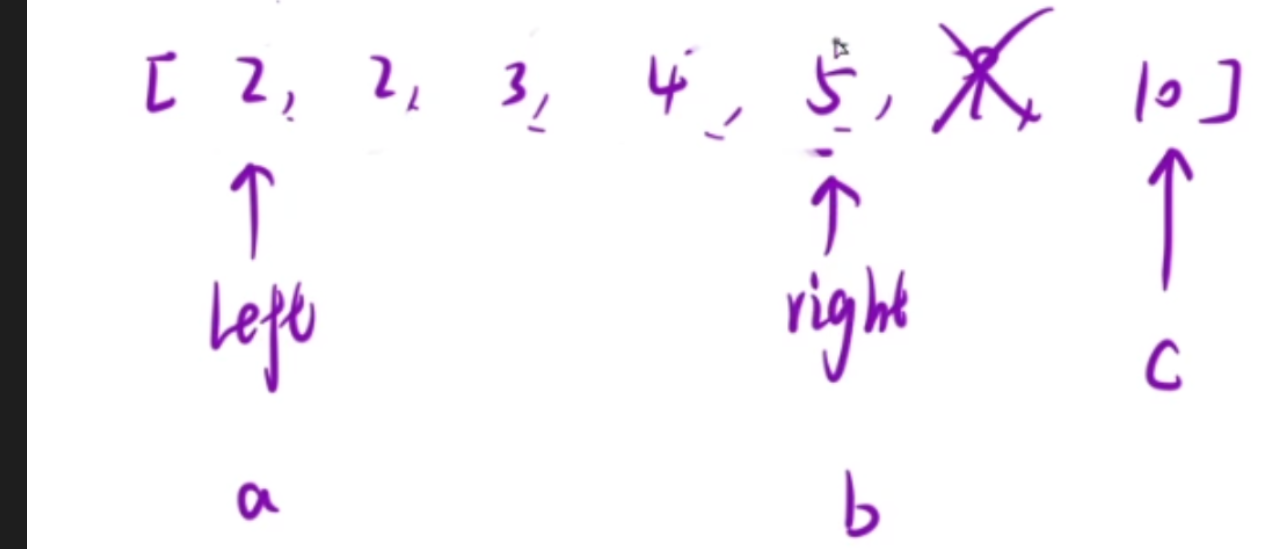

代码咋写？

咱们直接看代码，结合上面的思路理解：

class Solution {
public:int triangleNumber(vector<int>& nums) {// 先给数组排序，方便用a ≤ b ≤ c的条件sort(nums.begin(), nums.end());int n = nums.size() - 1;  // 从最大的数开始当cint sum = 0;  // 统计总共有多少个有效三元组// 当n至少为2时才有可能组成三元组（因为需要三个数）while (n >= 2) {int left = 0;    // 左指针，找较小的aint right = n - 1;  // 右指针，找中间的b// 当left < right时，继续找a和bwhile (left < right) {// 如果a + b > c，说明left到right-1的a都满足条件if (nums[left] + nums[right] > nums[n]) {sum += right - left;  // 加上这些符合条件的数量right--;  // 让b小一点，再试试} else {// 如果a + b ≤ c，说明a太小了，换个大一点的aleft++;}}n--;  // 换一个小一点的c}return sum;}
};