机器学习——聚类kmeans算法详解

一、聚类算法简介

1. 聚类算法是一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中
2. 在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法
   
3. 聚类算法分类：

• 根据聚类颗粒度分类：
  

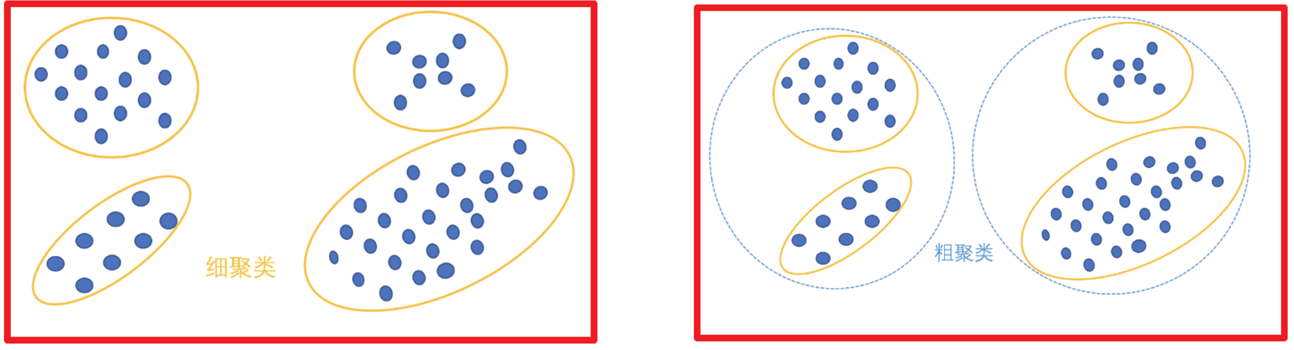
• 根据实现方法分类：

  • KMeans：按照质心分类
  • 层次聚类：对数据进行逐层划分，直到达到聚类的类别个数
  • DBSCAN聚类：一种基于密度的聚类算法
  • 谱聚类：一种基于图论的聚类方法

二、KMeans实现流程

1. 随机设置K个特征空间内的点作为初始的聚类中心
2. 对于其他每个嗲你计算到K个中心聚类，未知的点选择最近的一个聚类中心作为标记类别
3. 接着对着标记的聚类重心之后，重新计算出每个聚类的新中心点（平均值）
4. 如果计算得出的新中心点与原中心点一样（质心不在移动），那么结束，否则重新进行第二步的步骤
   

假设有如下数据，现在希望将数据划分为两类

1. 随机设置K个空间内的点作为初始的聚类中心（例子中选择2个，分别为P1和P2）

2. 对于其他每个店计算到K个中心的距离，未知的点选择最近的一个聚类中心作为标记类别
   

3. 重新计算出每个聚类的新中心点（平均值）

4. 如果计算得出的新中心点与原中心点一致（质心不再移动），则结束。否则重复第二步计算
   

5. 当每次迭代结果不变时，认为算法收敛，聚类完成

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets._samples_generator import make_blobs
from sklearn.metrics import calinski_harabasz_score
# 创建数据集
x,y = make_blobs(n_samples=100, n_features=2, centers=[[-1,-1],[0,0],[1,1],[2,2]], cluster_std=[0.4,0.3,0.1,0.2],random_state=22)
plt.scatter(x[:,0], x[:,1], marker='o')
plt.show()
# 使用KMeans聚类
y_pre = KMeans(n_clusters=4,random_state=22).fit_predict(x)
plt.scatter(x[:,0], x[:,1], c=y_pre)
plt.savefig('KMeans.png')
plt.show()
# 使用CH方法评估
print(calinski_harabasz_score(x, y_pre))

三、评价指标

3.1 SSE——误差平方和

1. 公式：$$SSE=\sum _{i=1}^{\mathrm{k}}\sum _{p\in C_i}{\left|p-m_i\right|}^2$$

• 其中K表示聚类中心的个数
• $C_i$表示簇
• $p$表示样本
• $m_i$表示簇的质心
  

2. SSE越小，表示数据点越接近他们的中心，聚类效果越好

3.2 SC系数——分离度（Separation）和凝聚度（Cohesion）

1. 公式：$$\mathrm{S}=\frac{(b-a)}{\max (a,b)},S\in [-1,1]$$

• 其中 a 表示样本 i 到同一簇内其他店不想死成都平均值，a 越小，说明它越属于这个簇
• b 表示样本 i 到其他簇的平均不相似程度的最小值，b 越大，说明它离其他簇越远

2. 特性：

• S 接近1：代表聚类效果好。样本与同簇的其他样本很接近（内聚度高），且远离其他簇的样本（分离度好）
• S 接近0：聚类效果一般。簇与簇之间的界限不清晰
• S 接近-1：聚类效果差。样本可能被分错了簇
  

3.3 CH系数——簇内离散度和簇间离散度

1. 公式：
   $$\begin{array}{rl}& \mathrm{CH}(\mathrm{k})=\frac{SSB}{SSW}\frac{m-k}{k-1}\\ & SSW=\sum _{i=1}^m{\Vert x_i-C_{pi}\Vert }^2\\ & SSB=\sum _{j=1}^k{n}_j{\Vert C_j-\bar{X}\Vert }^2\end{array}$$

• SSW:
  • $C_{pi}$表示质心
  • $x_i$表示某个样本
  • $SSW$值是计算每个样本点到质心的距离，并累加起来
  • $SSW$表示簇内的内聚程度，越小越好
  • $m$表示样本数量
  • $k$表示质心个数
• SSB：
  • $C_j$表示质心，$X$表示质心与质心之间的中心点，$n_j$表示样本个数
  • $SSB$表示簇与簇之间的分离度，$SSB$越大越好

3.4 肘部法

肘部法可以用来确定 K 值.

• 对于n个点的数据集，迭代计算 k from 1 to n，每次聚类完成后计算 SSE

• SSE 是会逐渐变小的，因为每个点都是它所在的簇中心本身

• SSE 变化过程中会出现一个拐点，下降率突然变缓时即认为是最佳 n_clusters 值

• 在决定什么时候停止训练时，肘形判据同样有效，数据通常有更多的噪音，在增加分类无法带来更多回报时，我们停止增加类别
  

四、案例

已知：客户性别、年龄、年收入、消费指数

需求：对客户进行分析，找到业务突破口，寻找黄金客户

数据集共包含顾客的数据, 数据共有 4 个特征, 数据共有 200 条。接下来，使用聚类算法对具有相似特征的的顾客进行聚类，并可视化聚类结果。

import matplotlib.colors
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScalerpd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
pd.set_option('display.width', 1000)if __name__ == '__main__':# 1. 读取顾客数据data = pd.read_csv('data/customers.csv')data.columns = ['CustomerID', 'Gender', 'Age', 'Annual Income', 'Spending Score']# print(data.head())# 2. 对 Gender 特征进行独热编码data = pd.get_dummies(data, columns=['Gender'])# print(data.head())# 3. 数据标准化scaler = StandardScaler()data = scaler.fit_transform(data)print(data)# 4. 去除非 ID 列进行聚类分析data = data[:, 1:]# print(data[:5])# 5. 肘部法寻找质心个数sse = []for k in range(1, 20):estimator = KMeans(n_clusters=k, random_state=0)estimator.fit(data)sse.append(estimator.inertia_)plt.plot(range(1, 20), sse)plt.show()# 6. 确定质心的个数estimator = KMeans(n_clusters=10, n_init=10, random_state=0)y_pred = estimator.fit_predict(data)# 7. 聚类结果可视化plt.scatter(X.values[y_kmeans == 0, 0], X.values[y_kmeans == 0, 1], s=100, c='red', label='Standard')    		plt.scatter(X.values[y_kmeans == 1, 0], X.values[y_kmeans == 1, 1], s=100, c='blue', label='Traditional')  plt.scatter(X.values[y_kmeans == 2, 0], X.values[y_kmeans == 2, 1], s=100, c='green', label='Normal')  plt.scatter(X.values[y_kmeans == 3, 0], X.values[y_kmeans == 3, 1], s=100, c='cyan', label='Youth')plt.scatter(X.values[y_kmeans == 4, 0], X.values[y_kmeans == 4, 1], s=100, c='magenta', label='TA')plt.scatter(mykeans.cluster_centers_[:, 0], mykeans.cluster_centers_[:, 1], s=300, c='black', label='Centroids’)plt.title('Clusters of customers')plt.xlabel('Annual Income (k$)')plt.ylabel('Spending Score (1-100)')   plt.legend() plt.show()