当前位置：首页 > news >正文

C语言数据结构-二叉树

news 2025/10/1 16:36:21

1. 树

1.1 树的概念及结构

1.1.1 树的概念

树是一种非线性数据结构,由有限个节点组合成具有层次关系的集合

根节点:树之中唯一没有父节点的节点,被称为该树所有节点的父节点
树是由递归定义的
除根节点外,其余结点互不相交,每个节点有且只有一个前驱节点
子树之间不能由任何的交集

1.1.2 树的相关知识

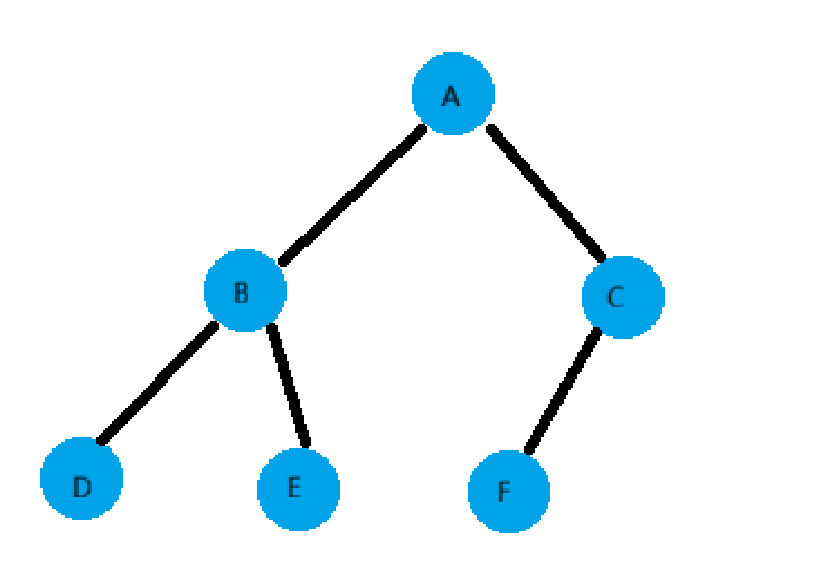
节点的度：一个节点含有的子树的个数称为该节点的度,如上图,A的度为4,B的度为3
叶子节点或终端节点：度为0的节点称为叶节点例如D
分支节点或非终端节点:度不为0的结点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点
兄弟节点:拥有相同的父节点的节点成为兄弟节点
树的度：一棵树中，最大的节点的度称为树的度,如上图树的度为4
节点的层次:一般以根节点为1,第二层为2,一次计算,少部分以根节点为0开始计算,推荐使用根节点为1计算
树的高度或深度：树中节点的最大层次,上图树的层次为3
堂兄弟节点：双亲在同一层的节点互为堂兄弟节点
森林:由多棵互不交集的树组成的集合叫做森林

1.1.3 树的表示方法

树的表示方法有很多种,例如:父子指针法,孩子-兄弟”表示法,左孩子—右兄弟表示法,父子指针矩阵等,然而我们较为频繁使用的是左孩子右兄弟表示法

typedef int DataType;struct Node{struct Node* _firstChild;//指向第一个孩子节点struct Node* _pNextBrother;//指向兄弟节点DataType _data; //保存数据              
};

2. 二叉树

2.1 二叉树的概念及结构

二叉树是有限节点的集合,二叉树具有以下特征:

由一个根节点加上两棵别称为左子树和右子树的二叉树组成
该树的度最大为2
当度为0时,依旧为二叉树,不过此时是一个空树
二叉树的左右子树顺序不能交换,说明二叉树是一颗有序树
二叉树所有情况:空树,只有左子树,只有右子树,左右子树都存在
现实之中的二叉树:

2.2 二叉树的遍历方式

二叉树的遍历方式一共有四种,可以按照两个方式划分为深度优先和广度优先:

深度优先:

前序遍历(根,左子树,右子树)
中序遍历(左子树,根,右子树)
后序遍历(左子树,右子树,根)
广度优先:
层序遍历(按照一层一层的遍历方式)

以2.1的图进行展示:

前序遍历:A,B,D,NULL,NULL,E,C,F,NULL,NULL,NULL
中序遍历:NULL,D,NULL,B,E,NULL,NULL,A,C,F,NULL,NULL,NULL
后序遍历:NULL,NULL,D,E,B,NULL,NULL,F,NULL,C,A
层序遍历:A,B,C,D,E,F,NULL,NULL,NULL,NULL,NULL,NULL,NULL

遍历时以叶子节点的左右子树也要计算
深度遍历的三种方式的思维是一样的,只是递归调用时的顺序不一样

//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL)//如果root等于空{printf("NULL ");//提示为空return;//结束函数}printf("%c ", root->_data);//打印root对应的数据PrevOrder(root->_left);//递归调用左子树PrevOrder(root->_right);//递归调用右子树}

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL)//如果root等于空{printf("NULL ");//提示为空return;//结束函数}InOrder(root->_left);//递归调用左子树printf("%c ", root->_data);//打印root对应的数据InOrder(root->_right);//递归调用右子树
}

//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL)//如果root等于空{printf("NULL ");//提示为空return;//结束函数}PostOrder(root->_left);//递归调用左子树PostOrder(root->_right);//递归调用右子树printf("%c ", root->_data);//打印root对应的数据
}

剩下一个就是层序遍历的方式,而层序遍历是以队列的思想遍历的,队列具有先进先出的特性,层序遍历需要满足:

根先进队列
迭代时队列不能为空,当出了队头的数据时,需要将队头的左右孩子放进队列
直到队列为空,遍历结束

因为C语言没有队列,所以需要添加之前写的队列至现有项,并且需要在Queue.h之中前向声明避免报错
前向声明:

struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;//重定义BTNode*类型为QDataType

实现思路:

//层序遍历
void LevelOrder(BTNode* root)
{Queue q;//实例化队列qif (root == NULL)//如果根节点为空{QueueDestroy(&q);  // 如果根为空，销毁队列并返回return;//结束函数}QueuePush(&q, root);//先放根节点进去while (!QueueEmpty(&q))//如果队列不为空则继续循环{BTNode* front = QueueFront(&q);//找到队头数据QueuePop(&q);//将队头出数据printf("%d ", front->_data);//打印数据if (front->_left)//该节点的左孩子不为空{QueuePush(&q, front->_left);//那么他的左孩子入队列}if (front->_right)//如果他的右孩子不为空{QueuePush(&q, front->_right);//那么他的右孩子入队列}}QueueDestroy(&q);  // 销毁队列
}

2.3 特殊的二叉树

满二叉树:一个二叉树,如果每层的节点的度都达到了2,即度达到了最大值,这个二叉树即满二叉树,如果这个树的层数为k,那么该二叉树的节点个数为 2^k-1 (此处表示2的k次方减1)
完全二叉树:完全二叉树是满二叉树的变体,由满二叉树引申而来,具有很高的效率,完全二叉树之中层数k与节点个数n具有很强烈的数学关系,将在二叉树的性质介绍

2.4 二叉树的性质

若根节点的层数为1(以下皆以此作为前置条件)，则一棵非空二叉树的第i层最多由2^(i-1)个节点, 注意此为该层的节点个数,以上的** 2^k-1为整个二叉树的最大节点个数**
深度为h的二叉树的最大节点个数为2^h-1,此时为满二叉树
对于任何一颗二叉树如果其叶子节点(度为0)个数为n0,分支节点(度为2)个数为n2,那么则有 n0=n2+1,叶子结点的个数始终将比分支节点多1
既然可以从层数推出节点个数,那么一定可以反向推理,从节点个数推理出二叉树层数:具有n个结点的满二叉树的深度为****log2⁽ⁿ⁺¹⁾
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序(数组的顺序方式)对所有节点从0(元素索引以0开始)开始编号，则对于序号为i的结点有：

若i > 0，i位置节点的父节点序号：(i-1)/2
若 i = 0，i为根节点编号，无父节点
若2i+1 < n(该节点说明存在孩子节点)，左孩子序号：2i+1(左孩子在右孩子的左边,按照数组顺序,左孩子比右孩子小1)，2i+1 >= n否则无左孩子
若2i+2 < n(该节点说明存在孩子节点)，右孩子序号：2i+2(左孩子在右孩子的左边,按照数组顺序,左孩子比右孩子小1)，2i+2 >= n否则无右孩子

如果该树有N个节点,高度为h的话,可以推出:
6. 满二叉树:2^h-1=N;
7. 完全二叉树:2^h-1-x=N , x的取值范围 [0,2 ^(h-1)-1];
8. 满二叉树的高度:log2^(N+1);
9. 完全二叉树的高度:log2^N+1;

如果父亲的下标是i,那么:
9. 左孩子的下标是2i+1;
10. 右孩子的下标是2i+2;

如果孩子的下标是i,那么:
11. 父节点的下标是 (i-1)/2

2.5 二叉树的顺序结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

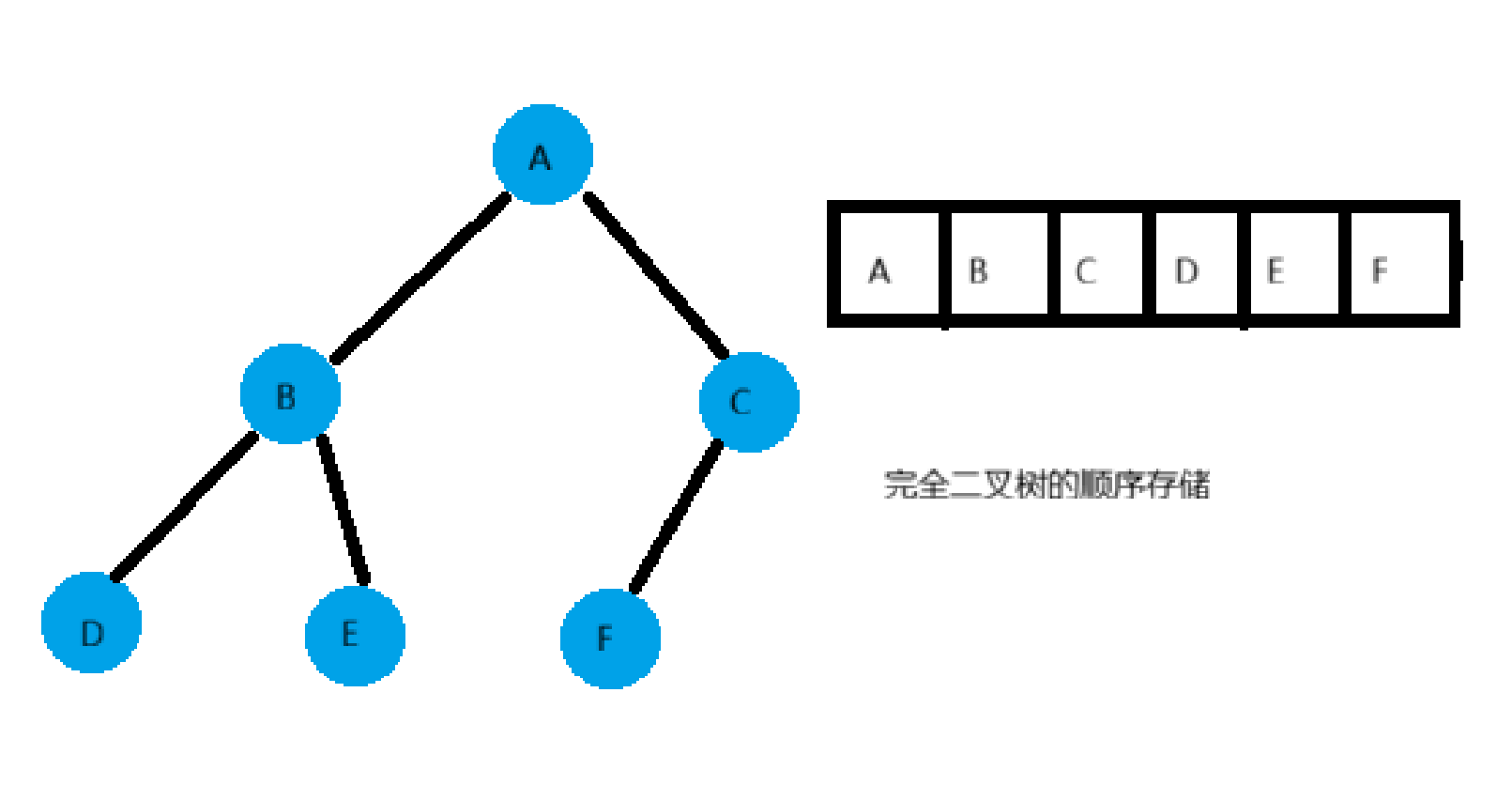
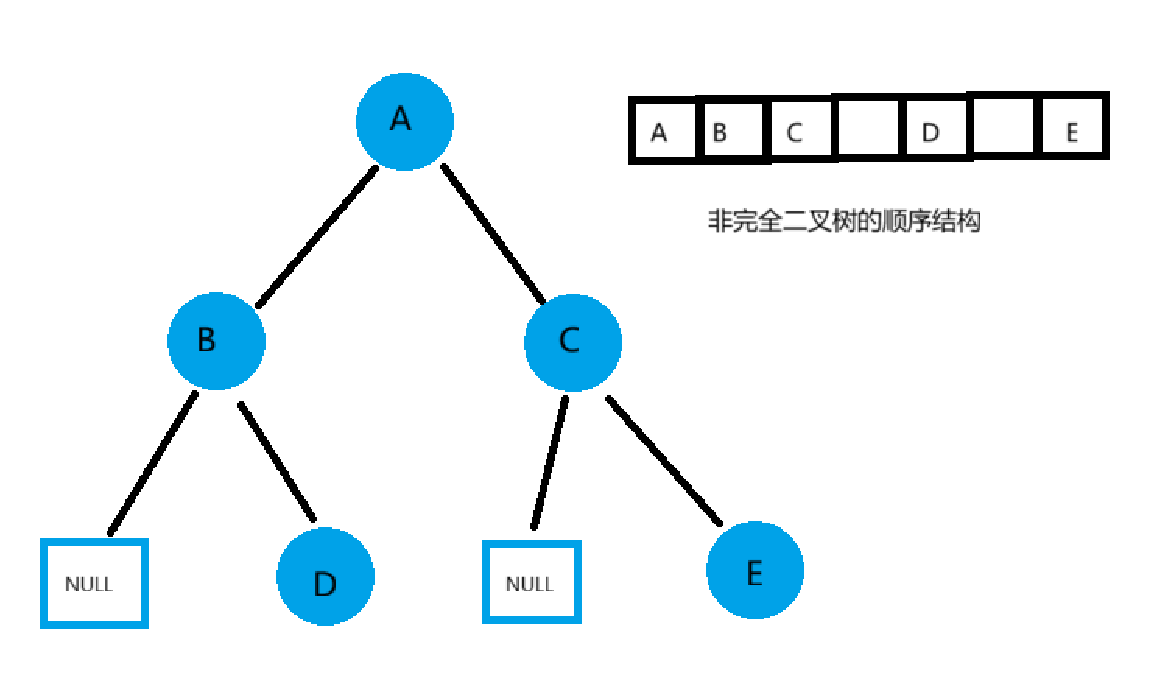
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树(完全二叉树是特殊类型的满二叉树)，因为不是完全二叉树会有空间的浪费**,堆结构通常使用顺序存储**。
而现实中使用中只有堆才会使用数组来存储，二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
我们一般情况下很少使用顺序结构进行存储,可能会消耗较多的空间,但是涉及到堆时会使用顺序结构

二叉树的顺序结构的代码将在C语言数据结构-堆展示

2.6 二叉树的链式结构

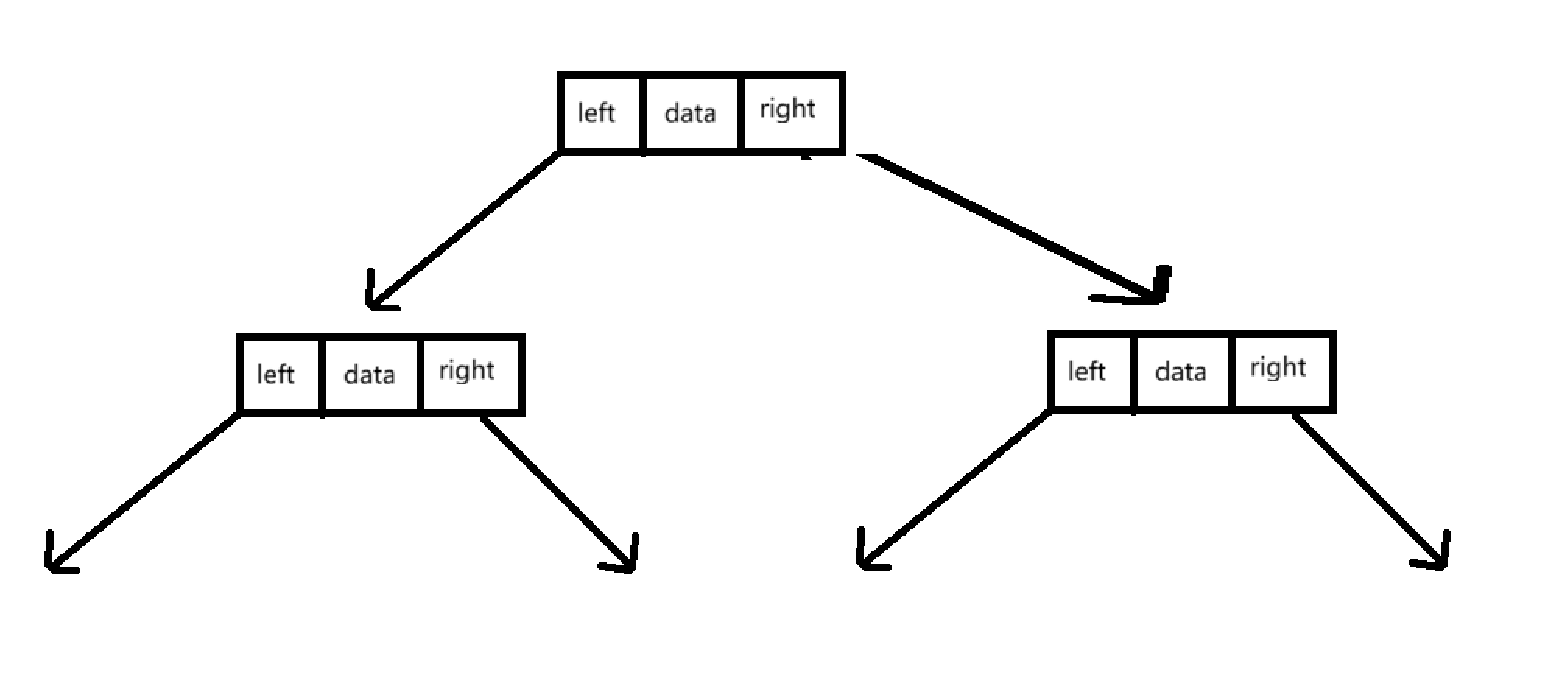
二叉树的链式结构是指使用链表对二叉树进行表示,通常每个节点由单个数据域对其进行表示,数据域,左指针域,右指针域,左右指针分别指向左右孩子的地址,链式结构一般有二叉链和三叉链,三叉链在红黑树之中会使用
在这里插入图片描述
二叉树的创建
本次演示的是二叉树的前序遍历创建,各种方式的创建思路是一样的,只是创建时递归调用的顺序不同

//前序遍历创建二叉树
BTNode* CreateTree(char* str, int* pi)//创建二叉树需要传递数组和数组下标
{if (str[*pi] == '#')//如果该数组下标为'#'说明该根/左子树/右子树为空{(*pi)++;//就算为空,数组下标依然需要加1,此处的pi为数组下标的地址需要解引用使用return NULL;//返回一个NULL,表示该根/左子树/右子树为空}else//否则的话,说明该下标的元素数据需要存储到二叉树之中{BTNode* root = (BTNode*)malloc(sizeof(BTNode));//需要创建一个相对的根节点if (root == NULL)//判断{perror("内存开辟失败\n");//提示exit(-1);//结束程序}root->_data = str[*pi];//使该数组储存到根节点之中(*pi)++;//数组下标加1root->_left = CreateTree(str, pi);//前序遍历创建,需要先调用左子树进入递归状态,此处的pi为数组下标的地址,无需解引用root->_right = CreateTree(str, pi);//然后调用右子树,总体顺序为根,左子树,右子树return root;//当二叉树创建完成,所有的递归结束,返回第一次调用的root根节点,即二叉树的根节点}
}

二叉树的销毁

//销毁二叉树
void DestroyTree(BTNode* root)
{if (root == NULL)//如果根节点为空{ return;//退出}DestroyTree(root->_left);//递归销毁左子树DestroyTree(root->_right);//递归销毁右子树free(root);//释放根节点// 不需要 root = NULL; 因为这是局部变量
}

2.7 判断是否为完全二叉树

判断是否为完全二叉树的方式是,完全二叉树通过层序递归遍历时从出现第一个NULL时到最后队列为空的过程之中队列的数据全部为空,如果从出现NULL到队列结束出现了一个非NULL的数值,说明该二叉树为非完全二叉树

//判断二叉树是否为完全二叉树
//因为C语言之中没有bool类型,所以以返回1为完全二叉树,返回0为非完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;//实例化队列qif (root == NULL);//如果根节点为空{return;//结束函数}QueuePush(&q, root);//先放根节点进去while (!QueueEmpty(&q))//如果队列不为空则继续循环{BTNode* front = QueueFront(&q);//找到队头数据QueuePop(&q);//将队头出数据if (front->_data == NULL)//如果发现出队列的数据发现了NULL{break;//就跳出循环}//如果没有发现NULL的话QueuePush(&q, front->_left);//将左孩子入队列QueuePush(&q, front->_right);//将右孩子入队列}//当以上发现了NULL时,跳出了循环就进入以下循环判断出现NULL之后的队列之中是否存在非NULL// 如果存在就说明该二叉树为非完全二叉树,如果没有存在,全是空说明是完全二叉树while (!QueueEmpty(&q))//如果队列不为空{BTNode* front = QueueFront(&q);//找到队头QueuePop(&q);//出队头数据if (front != NULL)//如果剩下的队列之中有一个数据不为空{QueueDestory(&q);//销毁队列return 0;//返回0,提示非完全二叉树}}return 1;//否则返回1
}