解码数据结构树

树的基本概念与核心术语

树是计算机科学中重要的非线性数据结构，其逻辑关系呈 “一对多” 层次结构，广泛应用于层级数据组织（如公司架构、族谱、文件系统）。

树的定义

树是由n（n≥0）个节点组成的有限集，分为两种情况：

空树：n=0，即没有任何节点的树；

非空树：需满足两个条件：

• 存在唯一的 “顶层” 节点，称为根节点（Root），它没有直接前驱（没有 “父节点”）；
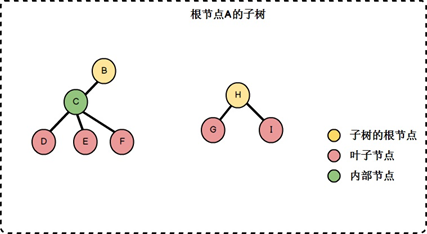
• 除根节点外，其余节点可分为m（m≥0）个互不相交的有限集T₁、T₂、…、Tₘ，每个集合本身也是一棵树，称为根节点的子树（Subtree）。

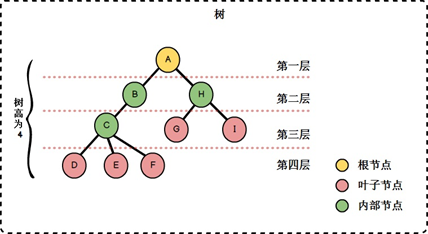
树的术语（结合 “家族树” ）

术语	定义（通俗解释）	例子
双亲 / 孩子	若节点 A 是子树 T 的根，则 A 是 T 中所有节点的双亲（Parent），T 中节点是 A 的孩子（Child）	家族中父母与子女的关系，如根节点 A 有子树 T₁（根为 B），则 A 是 B 的双亲，B 是 A 的孩子
兄弟	同一双亲的多个孩子之间互称兄弟（Sibling）	同一父母的子女，如 A 的孩子 B 和 H 是兄弟
祖先 / 子孙	从根到某节点的路径上所有节点是该节点的祖先；某节点子树中的所有节点是该节点的子孙	节点 D 的祖先为 A、B、C（路径 A→B→C→D）；B 的子孙为 C、D、E、F
度	节点拥有的子树数量（即孩子数量）	节点 A 有 2 个孩子（B、H），则 A 的度为 2；叶子节点度为 0
叶子节点	度为 0 的节点（没有孩子，是 “最底层” 节点），也叫终端节点	节点 D、E、F、G、I（没有子树）
分支节点	度不为 0 的节点（有至少一个孩子），也叫非终端节点（根节点可能是分支节点）	节点 A、B、H、C（都有子树）
层次	根节点为第 1 层，其子节点为第 2 层，以此类推（部分教材从 0 层开始，需注意场景）	根 A（1 层）→ 孩子 B、H（2 层）→ 孙子 C、G（3 层）→ 曾孙 D、E、F、I（4 层）
深度 / 高度	树的最大层次（即 “最深” 节点的层次），深度和高度在树中通常同义	上述树的最大层次是 4，故深度（高度）为 4

二叉树的定义与常见类型

二叉树是树的特殊形式，也是实际应用中最广泛的树结构，其核心特点是 “有序” 且 “子树数量有限”。

二叉树的定义

二叉树是n（n≥0）个节点的有限集，每个节点至多有 2 棵子树（度≤2），且子树有明确的左右顺序 —— 分别称为左子树（Left Subtree） 和右子树（Right Subtree），即使只有一棵子树，也需区分 “左” 或 “右”。

• 空二叉树：n=0；

• 非空二叉树：可分为 5 种基本形态：

  

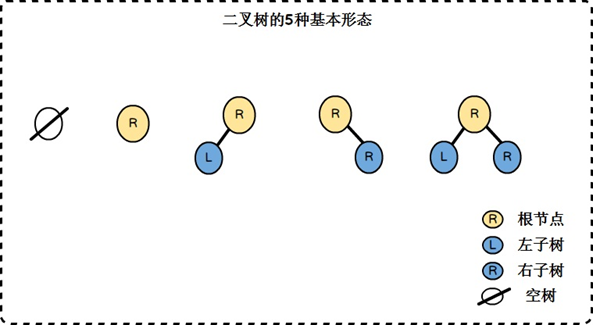
常见二叉树类型

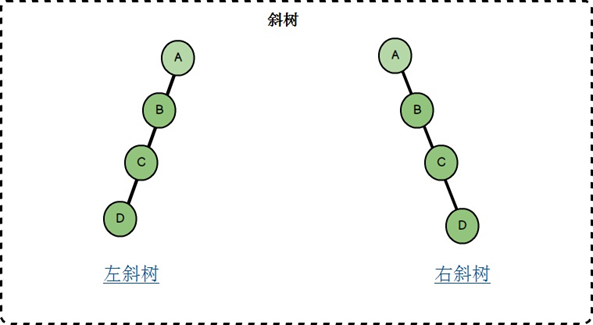
斜树

• 所有节点都只有左子树（左斜树）或只有右子树（右斜树），本质上退化为线性结构（类似链表），无法体现二叉树的高效性。
  

满二叉树

• 定义：高度为h的二叉树，节点总数为2ʰ - 1（每一层的节点数都达到最大值）；

• 特点：

  • 所有分支节点的度均为 2（每个节点都有左、右子树）；
  • 叶子节点全部集中在最底层（第h层）；
  • 满二叉树的节点数是同高度二叉树中最多的。

  

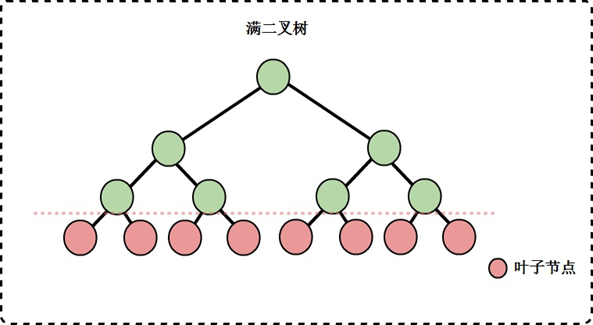
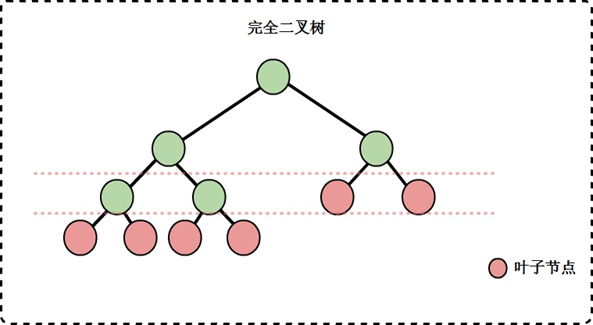
完全二叉树

• 定义：按 “从上到下、从左到右” 的顺序给节点编号，若编号为i的节点与 “高度相同的满二叉树” 中编号i的节点位置完全一致，则为完全二叉树；

• 核心特点：

  • 只有最底层的节点可能不满，且最底层的叶子节点全部集中在左侧；
  • 除最底层外，其他层的节点数均为最大值（即满二叉树的对应层节点数）；

• 关系：满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树

  

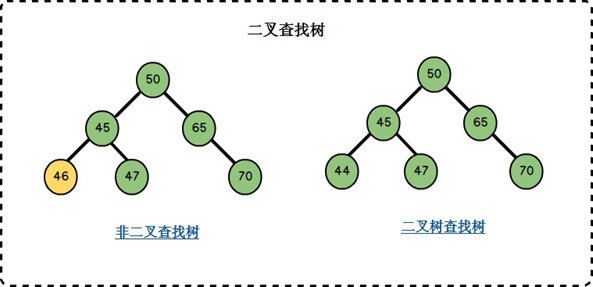
二叉查找树（BST，Binary Search Tree）

又称二叉排序树，是 “支持高效查找、插入、删除” 的二叉树，核心是节点键值（key）的有序性：

• 性质：

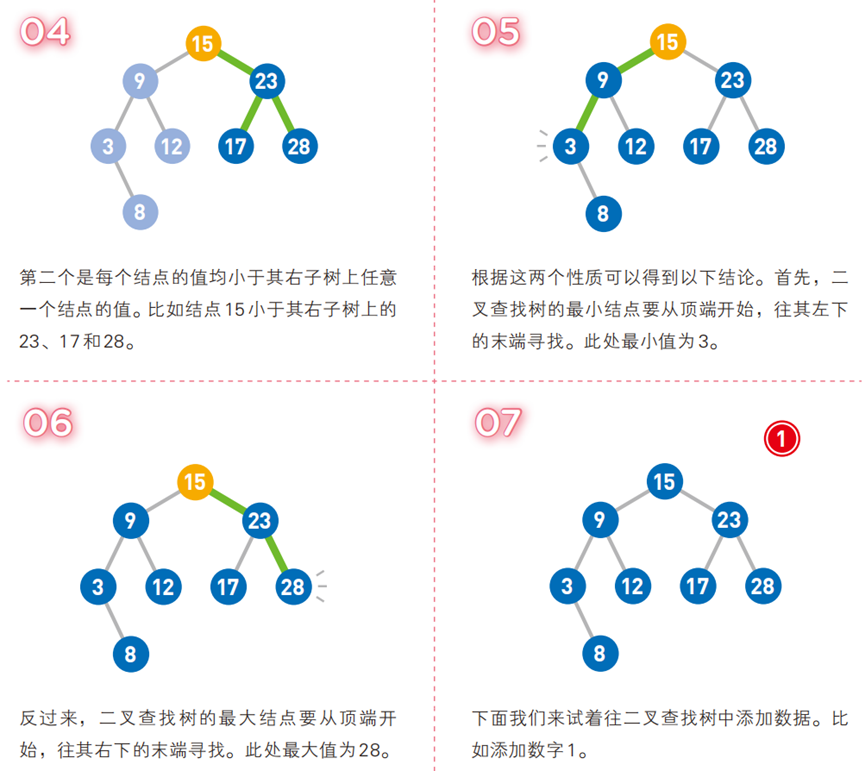
  • 若左子树非空，则左子树中所有节点的键值 < 根节点的键值；
  • 若右子树非空，则右子树中所有节点的键值 > 根节点的键值；
  • 左、右子树也分别是二叉查找树（递归性质）；
  • 节点键值唯一（无重复）。

  

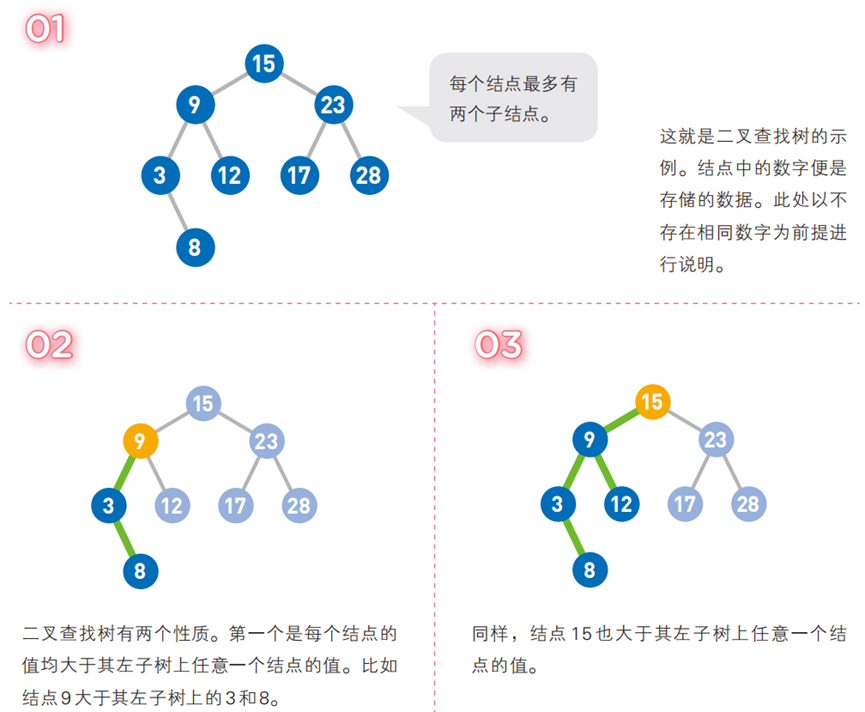
• 图解二叉排序树与操作示例

  

  

  

  

  

  

  

  

  

  

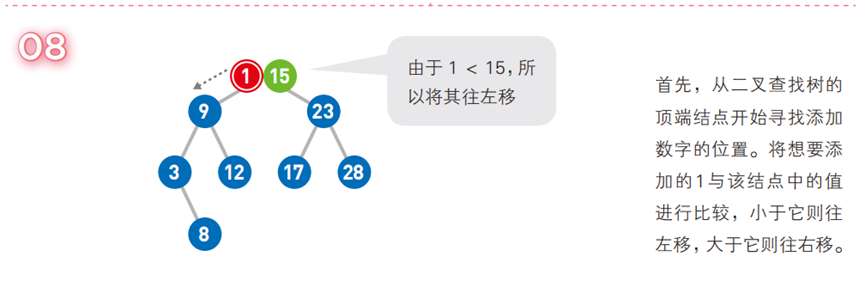
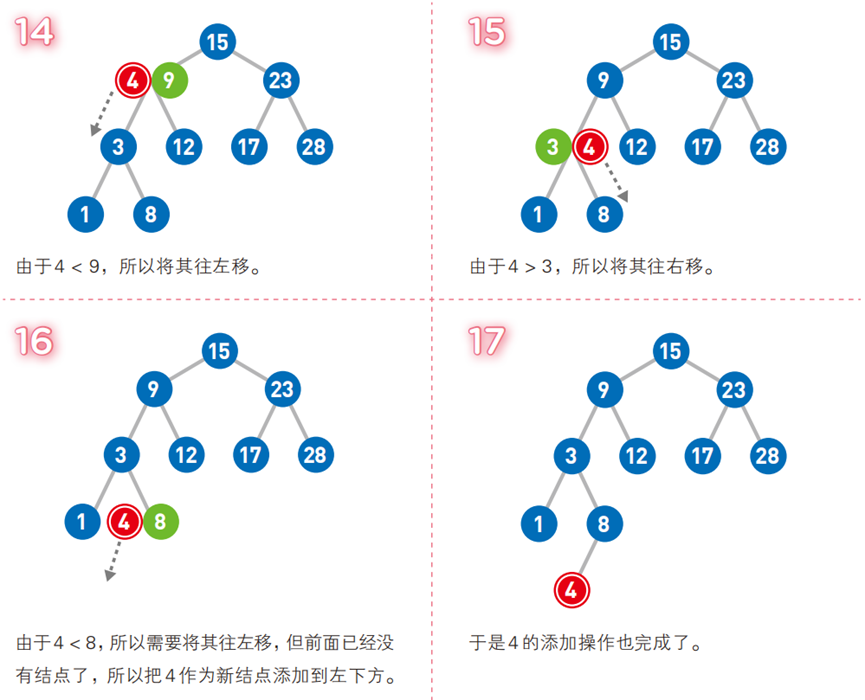
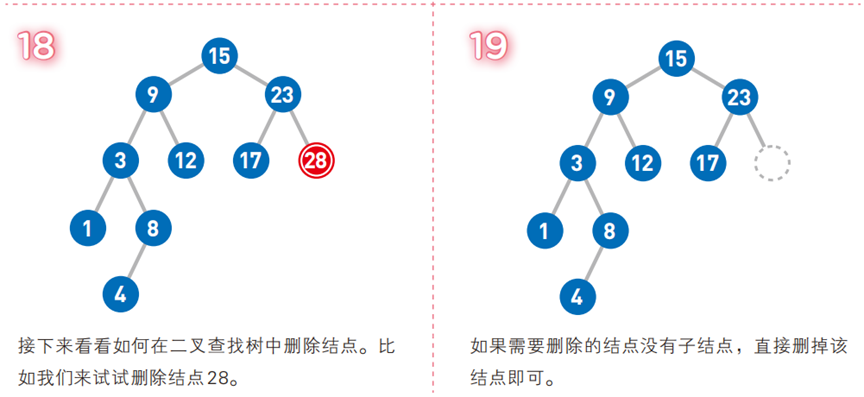
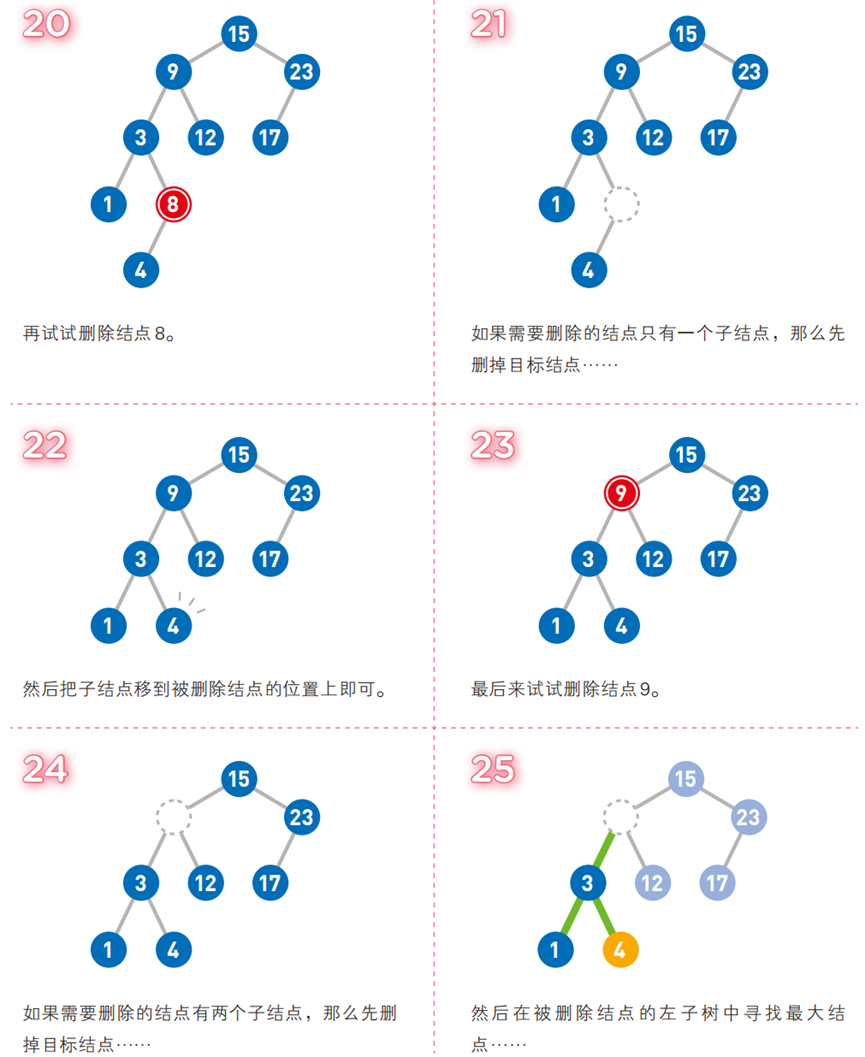
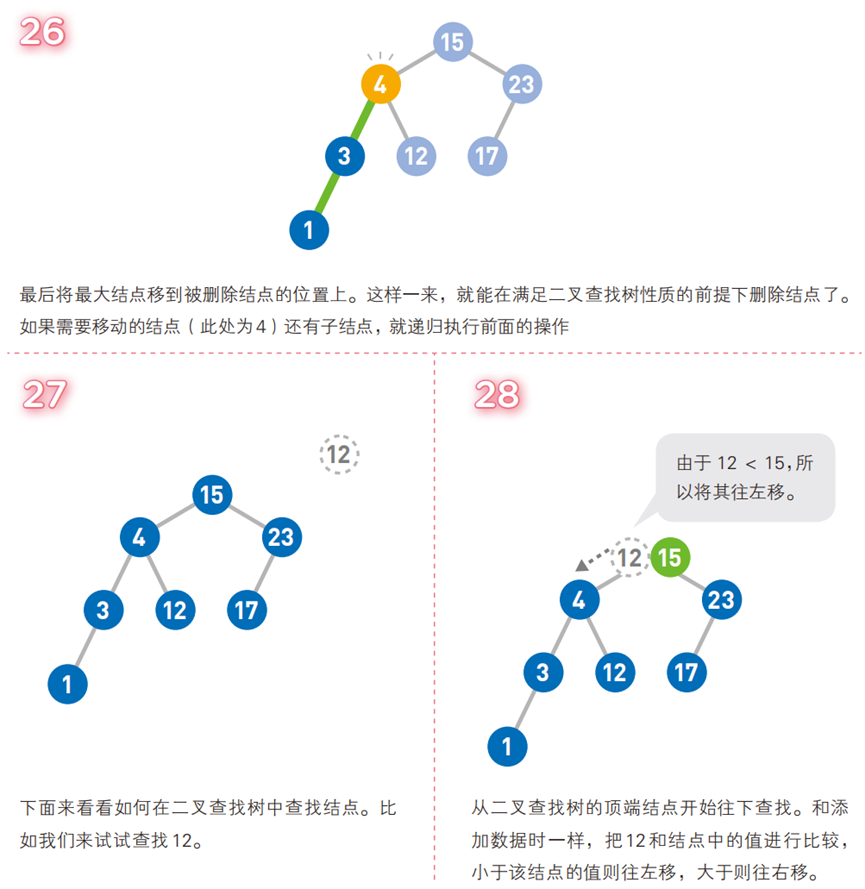
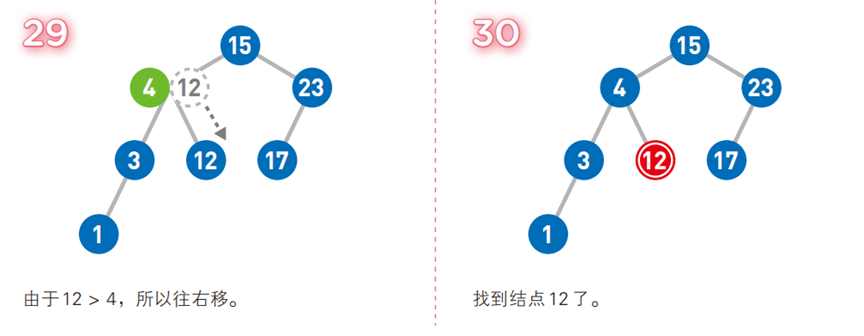
• 优势：查找、插入、删除的平均时间复杂度为O(logn)（类似二分查找）；若退化为斜树，时间复杂度会变为O(n)（需平衡二叉树优化）。

平衡二叉树（AVL 树）

为解决二叉查找树退化为斜树的问题，平衡二叉树在 BST 的基础上增加了 “平衡条件”：

• 定义：树中任意节点的左子树深度与右子树深度之差（平衡因子）的绝对值 ≤ 1（平衡因子 = 左子树深度 - 右子树深度，取值为 - 1、0、1）；

• 特点：始终保持树的 “平衡”，确保查找、插入、删除的时间复杂度稳定为O(logn)；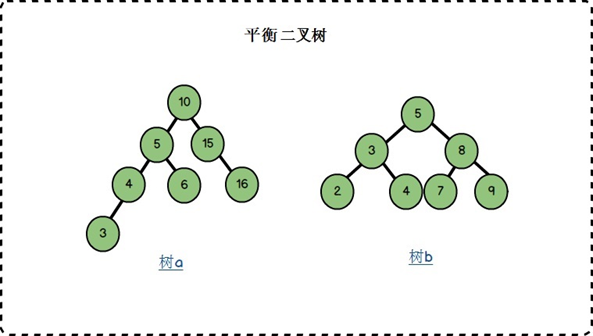

  

二叉树的重要性质

性质 1：叶子节点数 = 双分支节点数 + 1

• 符号定义：
  • n₀：叶子节点数（度为 0）；
  • n₁：单分支节点数（度为 1）；
  • n₂：双分支节点数（度为 2）；
  • 总节点数 n = n₀ + n₁ + n₂。
• 推导过程：
  1. 树的 “边数” = 总节点数 - 1（任意树中，边数比节点数少 1，如 2 个节点 1 条边）；
  2. 边数也可通过 “节点度” 计算：单分支节点贡献 1 条边，双分支节点贡献 2 条边，叶子节点贡献 0 条边，故边数 = n₁×1 + n₂×2；
  3. 联立得：n₁ + 2n₂ = (n₀ + n₁ + n₂) - 1，化简后 n₀ = n₂ + 1。

eg 1：有 10 个叶子节点的二叉树中，度为 2 的节点数是多少？

• 解析：由n₀ = n₂ + 1，得n₂ = n₀ - 1 = 10 - 1 = 9。

eg 2：一棵二叉树有 10 个度为 2 的节点，5 个度为 1 的节点，求叶子节点数？

• 解析：n₀ = n₂ + 1 = 10 + 1 = 11。

性质 2：第i层最多有2^(i-1)个节点（i≥1）

• 推导：第 1 层（根）最多 1 个节点（2⁰=1）；第 2 层最多 2 个节点（2¹=2）；第 3 层最多 4 个节点（2²=4）；每层节点数是上一层的 2 倍，故第i层最多2^(i-1)个。
• 例子：第 4 层最多2³=8个节点（与满二叉树第 4 层节点数一致）。

性质 3：高度为h的二叉树，最多有2ʰ - 1个节点（h≥1）

• 推导：总节点数是各层最大节点数之和，即1 + 2 + 4 + ... + 2^(h-1)，这是等比数列求和，结果为2ʰ - 1。
• 注意：此情况即 “满二叉树”（所有层节点数均为最大值）。

eg 3：高度为h的完全二叉树至多有多少个节点？

• 解析：完全二叉树的最大节点数即同高度满二叉树的节点数，故为2ʰ - 1。

eg 4：对一棵满二叉树，共有n个节点、m个叶子节点、高度h，下列正确的是？

• 解析：满二叉树节点数n=2ʰ - 1（性质 3）；叶子节点m=2^(h-1)（最底层节点数）。

性质 4：完全二叉树的节点编号特性

若完全二叉树节点按 “从上到下、从左到右” 编号（从 1 开始），则对编号为i的节点：

• 左孩子编号：2i（若2i ≤ n，否则无左孩子）；
• 右孩子编号：2i + 1（若2i + 1 ≤ n，否则无右孩子）；
• 父节点编号：i//2（i>1，若i=1则为根，无父节点）。
• 例子：编号 3 的节点，左孩子 6、右孩子 7；编号 5 的父节点 2。

二叉树的存储结构

存储二叉树需体现 “节点数据” 和 “左、右子树的逻辑关系”，常见两种存储方式：

顺序存储（数组存储）

原理

用一组地址连续的数组存储节点，按 “完全二叉树的编号顺序” 存放：编号为i的节点，存储在数组下标为i-1的位置（数组从 0 开始）；若节点不存在（非完全二叉树的空节点），用特殊值（如 0）标记。

适用场景

• 适合满二叉树、完全二叉树：无空间浪费，且可通过数组下标快速找到父 / 子节点（利用性质 4）；
• 不适合一般二叉树（如斜树）：会产生大量空位置（用 0 填充），严重浪费空间。

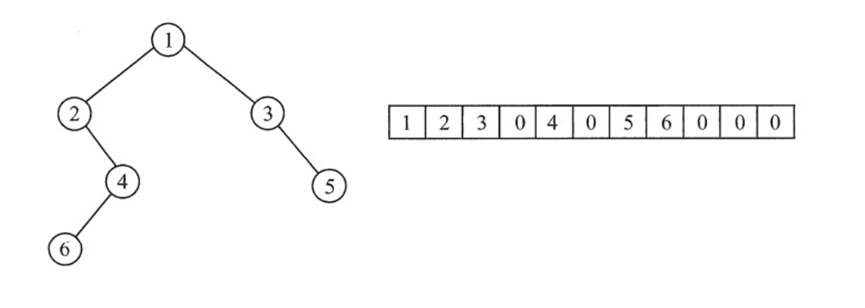
代码

// 定义宏：最大节点数（可根据需求调整）
#define MAX_SIZE 100
// 定义空节点标记（假设数据为整数，用-1表示空）
#define EMPTY -1// 顺序存储二叉树的结构体
typedef struct {int data[MAX_SIZE];  // 存储节点数据的数组int count;           // 当前节点总数
} SeqBinaryTree;// 初始化空的顺序二叉树
void InitSeqBinaryTree(SeqBinaryTree *tree) {if (tree == NULL) return;// 初始化所有位置为空for (int i = 0; i < MAX_SIZE; i++) {tree->data[i] = EMPTY;}tree->count = 0;  // 初始节点数为0
}// 插入节点（按完全二叉树的层次顺序插入，即"从上到下、从左到右"）
// 注：插入时需保证父节点已存在（根节点除外）
bool InsertNode(SeqBinaryTree *tree, int value) {if (tree == NULL) return false;// 检查是否已满if (tree->count >= MAX_SIZE) {printf("二叉树已满，无法插入\n");return false;}// 插入到数组的末尾（对应完全二叉树的下一个位置）tree->data[tree->count] = value;tree->count++;return true;
}// 获取节点的父节点（数组下标从0开始）
// 参数：节点在数组中的下标（index）
// 返回：父节点的值（空则返回EMPTY）
int GetParent(SeqBinaryTree *tree, int index) {if (tree == NULL || index < 0 || index >= tree->count) {return EMPTY;  // 下标无效}if (index == 0) {return EMPTY;  // 根节点（下标0）无父节点}// 父节点下标 = (当前下标 - 1) / 2（整数除法）int parentIndex = (index - 1) / 2;return tree->data[parentIndex];
}// 获取节点的左孩子
// 参数：节点在数组中的下标（index）
// 返回：左孩子的值（空则返回EMPTY）
int GetLeftChild(SeqBinaryTree *tree, int index) {if (tree == NULL || index < 0 || index >= tree->count) {return EMPTY;  // 下标无效}// 左孩子下标 = 2 * 当前下标 + 1int leftIndex = 2 * index + 1;if (leftIndex >= tree->count) {return EMPTY;  // 左孩子不存在}return tree->data[leftIndex];
}// 获取节点的右孩子
// 参数：节点在数组中的下标（index）
// 返回：右孩子的值（空则返回EMPTY）
int GetRightChild(SeqBinaryTree *tree, int index) {if (tree == NULL || index < 0 || index >= tree->count) {return EMPTY;  // 下标无效}// 右孩子下标 = 2 * 当前下标 + 2int rightIndex = 2 * index + 2;if (rightIndex >= tree->count) {return EMPTY;  // 右孩子不存在}return tree->data[rightIndex];
}// 层序遍历（按数组顺序访问非空节点，即层次顺序）
void LevelOrderTraversal(SeqBinaryTree *tree) {if (tree == NULL || tree->count == 0) {printf("二叉树为空\n");return;}printf("层序遍历结果：");for (int i = 0; i < tree->count; i++) {printf("%d ", tree->data[i]);}printf("\n");
}

链式存储（二叉链表）

原理

用 “链表节点” 存储每个元素，每个节点包含 3 个部分：

• 数据域：存储节点的值（如 key）；
• 左指针域：指向左孩子节点的地址；
• 右指针域：指向右孩子节点的地址；
• 若某子树不存在，指针域设为NULL。

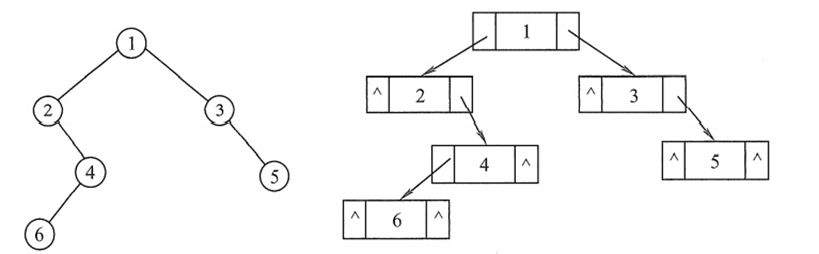
节点结构定义

// 二叉树节点结构体
typedef int DataType_t; // 数据类型（可根据需求修改）
typedef struct BSTnode {DataType_t data;          // 数据域struct BSTnode *lchild;   // 左孩子指针struct BSTnode *rchild;   // 右孩子指针
} BSTnode_t;

适用场景

• 适合所有二叉树，尤其是一般二叉树：无空间浪费，插入 / 删除时只需调整指针，无需移动大量元素；
• 缺点：无法像顺序存储那样快速查找父节点（需额外存储父指针，即 “三叉链表”，此处暂不展开）。

二叉树的遍历

遍历是 “按一定顺序访问二叉树所有节点，且每个节点仅访问一次”，是获取树中数据的核心操作。常见遍历方式分为 “深度优先” 和 “广度优先”。

深度优先遍历（DFS）

优先遍历子树（深入到最底层后再回溯），包括前序、中序、后序三种，核心是 “根节点的访问时机”。

前序遍历（根 → 左 → 右）

• 顺序：先访问根节点，再递归遍历左子树，最后递归遍历右子树；
• eg：前序序列为：A → B → D → G → H → E → I → C → F。

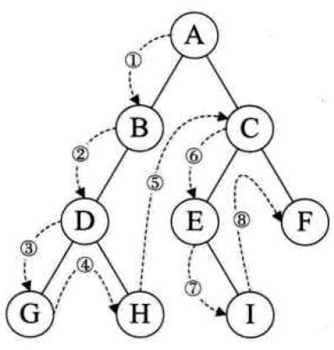
中序遍历（左 → 根 → 右）

• 顺序：先递归遍历左子树，再访问根节点，最后递归遍历右子树；
• 关键：二叉查找树的中序遍历序列是严格递增的（核心特性，用于验证 BST 正确性）；
• eg：中序序列为：G → D → H → B → I → E → A → F → C。

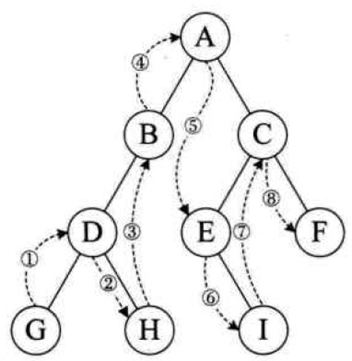
后序遍历（左 → 右 → 根）

• 顺序：先递归遍历左子树，再递归遍历右子树，最后访问根节点；
• eg：后序序列为：G → H → D → I → E → B → F → C → A。

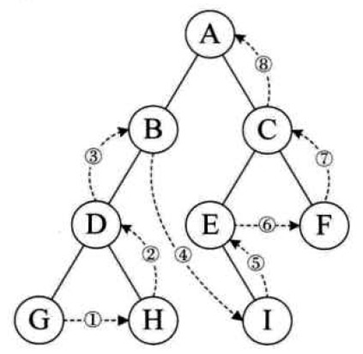
递归实现代码

// 前序遍历
void PreOrder(BSTnode_t *root) {if (root != NULL) {          // 若节点非空printf("%d ", root->data); // 访问根节点PreOrder(root->lchild);   // 遍历左子树PreOrder(root->rchild);   // 遍历右子树}
}// 中序遍历
void InOrder(BSTnode_t *root) {if (root != NULL) {InOrder(root->lchild);    // 遍历左子树printf("%d ", root->data); // 访问根节点InOrder(root->rchild);    // 遍历右子树}
}// 后序遍历
void PostOrder(BSTnode_t *root) {if (root != NULL) {PostOrder(root->lchild);  // 遍历左子树PostOrder(root->rchild);  // 遍历右子树printf("%d ", root->data); // 访问根节点}
}

广度优先遍历（BFS，层序遍历）

原理

按 “层次顺序” 访问节点（先访问第 1 层，再第 2 层，…，最后第h层），需借助队列实现（先进先出）：

• 初始化队列，将根节点入队；
• 若队列非空，出队队首节点并访问；
• 若该节点有左孩子，左孩子入队；若有右孩子，右孩子入队；
• 重复步骤 2~3，直到队列为空。

代码

// 二叉树节点结构体
typedef int DataType_t;
typedef struct BSTnode {DataType_t data;struct BSTnode *lchild;struct BSTnode *rchild;
} BSTnode_t;// 队列节点结构体（用于存储二叉树节点的指针）
typedef struct QueueNode {BSTnode_t *treeNode;       // 指向二叉树节点struct QueueNode *next;    // 指向队列中下一个节点
} QueueNode_t;// 队列结构体（队头+队尾指针）
typedef struct {QueueNode_t *front;        // 队头（出队端）QueueNode_t *rear;         // 队尾（入队端）
} Queue_t;// 初始化队列（创建空队列）
void Queue_Init(Queue_t *queue) {queue->front = NULL;queue->rear = NULL;
}// 入队操作（将二叉树节点指针加入队列）
void Queue_Enqueue(Queue_t *queue, BSTnode_t *treeNode) {// 创建新的队列节点QueueNode_t *newNode = (QueueNode_t *)malloc(sizeof(QueueNode_t));newNode->treeNode = treeNode;  // 存储二叉树节点指针newNode->next = NULL;if (queue->rear == NULL) {  // 队列空时，队头和队尾都指向新节点queue->front = newNode;queue->rear = newNode;} else {  // 队列非空时，新节点加到队尾queue->rear->next = newNode;queue->rear = newNode;}
}// 出队操作（取出队头的二叉树节点指针）
BSTnode_t *Queue_Dequeue(Queue_t *queue) {if (queue->front == NULL) {  // 队列为空，返回NULLreturn NULL;}// 保存队头节点QueueNode_t *temp = queue->front;BSTnode_t *treeNode = temp->treeNode;  // 取出二叉树节点指针// 更新队头queue->front = queue->front->next;if (queue->front == NULL) {  // 若队头为空，队尾也置空（队列变空）queue->rear = NULL;}free(temp);  // 释放队列节点的内存return treeNode;
}// 判断队列是否为空
bool Queue_IsEmpty(Queue_t *queue) {return (queue->front == NULL);
}// 层序遍历（广度优先遍历）
void LevelOrder(BSTnode_t *root) {if (root == NULL) {  // 空树，直接返回printf("二叉树为空，无法遍历\n");return;}Queue_t queue;Queue_Init(&queue);       // 初始化队列Queue_Enqueue(&queue, root);  // 根节点入队printf("层序遍历结果：");while (!Queue_IsEmpty(&queue)) {  // 队列非空时循环BSTnode_t *current = Queue_Dequeue(&queue);  // 出队队首节点printf("%d ", current->data);  // 访问当前节点// 左孩子入队（若存在）if (current->lchild != NULL) {Queue_Enqueue(&queue, current->lchild);}// 右孩子入队（若存在）if (current->rchild != NULL) {Queue_Enqueue(&queue, current->rchild);}}printf("\n");
}

eg

上述树的层序序列为：A → B → C → D → E → F → G → H → I。

由遍历序列还原二叉树

需至少两种遍历序列（其中一种是中序），核心是 “通过前序 / 后序找根，通过中序分左右子树”。

eg：已知前序序列ABDEGHCF，中序序列DBGEHACF，求后序序列。

• 步骤 1：前序第一个节点是根（A），在中序中划分左子树（DBGEH）和右子树（CF）；
• 步骤 2：处理左子树（前序BDEGH，中序DBGEH）：
  • 前序第一个节点是左子树根（B），中序分左子树（D）和右子树（GEH）；
  • 左子树D（前序D，中序D）：叶子节点；
  • 右子树GEH（前序EGH，中序GEH）：根E，左子树G，右子树H；
• 步骤 3：处理右子树（前序CF，中序CF）：
  • 前序第一个节点是右子树根（C），中序右子树（F）：叶子节点；
• 步骤 4：还原树后，后序序列为D → G → H → E → B → F → C → A。

二叉查找树（BST）的核心操作

BST 的操作需始终保持 “左子树 key < 根，右子树 key> 根” 的性质，以下基于链式存储实现。

BST 的节点创建与树初始化

// 创建新节点
BSTnode_t *BSTree_NewNode(DataType_t data) {BSTnode_t *newNode = (BSTnode_t *)calloc(1, sizeof(BSTnode_t)); // 申请内存并初始化0if (newNode == NULL) {perror("内存申请失败");return NULL;}newNode->data = data;    // 赋值数据newNode->lchild = NULL; // 左指针初始为空newNode->rchild = NULL; // 右指针初始为空return newNode;
}// 初始化BST（创建根节点）
BSTnode_t *BSTree_Create(DataType_t rootVal) {return BSTree_NewNode(rootVal); // 根节点即新创建的节点
}

BST 的插入操作

思路

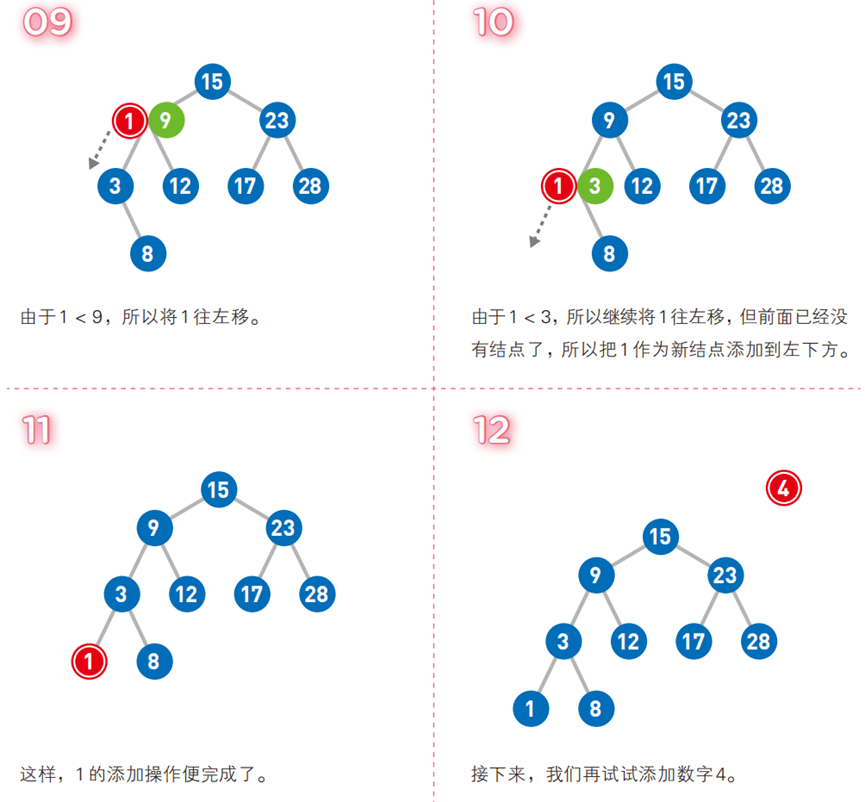
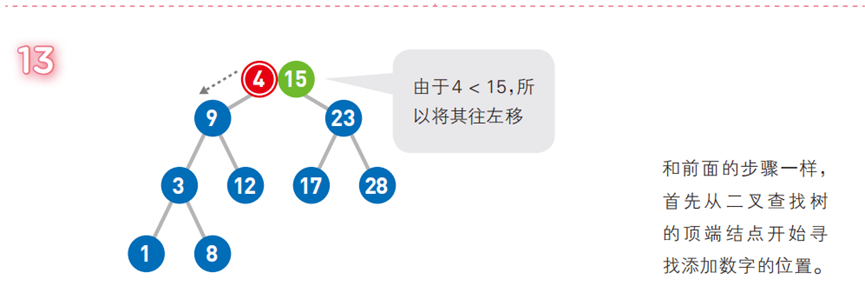
• 若树为空，直接将新节点作为根；
• 若树非空，从根开始比较：
  • 新节点 key < 当前节点 key：若左子树为空，插入左子树；否则递归左子树；
  • 新节点 key > 当前节点 key：若右子树为空，插入右子树；否则递归右子树；
  • （key 相等时，BST 通常不允许重复，直接返回）。

代码实现

BSTnode_t *BSTree_Insert(BSTnode_t *root, DataType_t data) {if (root == NULL) {          // 树空，插入新节点return BSTree_NewNode(data);}if (data < root->data) {     // 新数据小，插入左子树root->lchild = BSTree_Insert(root->lchild, data);} else if (data > root->data) { // 新数据大，插入右子树root->rchild = BSTree_Insert(root->rchild, data);}return root; // 数据相等，不插入，返回原根
}

BST 的查找操作

思路

• 若树为空或当前节点 key 等于目标 key，返回当前节点；
• 若目标 key < 当前节点 key，递归查找左子树；
• 若目标 key > 当前节点 key，递归查找右子树。

代码实现

BSTnode_t *BSTree_Search(BSTnode_t *root, DataType_t target) {if (root == NULL || root->data == target) { // 空树或找到目标return root;}if (target < root->data) { // 目标小，查左子树return BSTree_Search(root->lchild, target);} else { // 目标大，查右子树return BSTree_Search(root->rchild, target);}
}

BST 的删除操作（重点）

删除需分 3 种情况，核心是 “删除后保持 BST 性质”。

情况 1：删除的节点是叶子节点（无左、右子树）

• 操作：直接删除该节点，将其双亲的对应指针（左 / 右）设为NULL；
• 例子：删除叶子节点G，只需将D的左指针设为NULL，释放G。

情况 2：删除的节点有一个子节点（左或右）

• 操作：用该节点的子节点 “替换” 被删除节点（即让被删除节点的双亲指向其子节点），释放被删除节点；
• 例子：删除节点E（只有右子树I），将B的右指针指向I，释放E。

情况 3：删除的节点有两个子节点（左、右子树均非空）

• 核心思路：找 “替代节点”（保持 BST 性质），有两种选择：
  • 左子树的最大节点（左子树中最右侧的节点，该节点无右子树）；
  • 右子树的最小节点（右子树中最左侧的节点，该节点无左子树）；
• 操作步骤（以左子树最大节点为例）：
  • 找到被删除节点左子树的最大节点（记为tmp）；
  • 将tmp的数据赋值给被删除节点（覆盖，相当于 “替换”）；
  • 递归删除tmp（tmp最多有一个子节点，按情况 1 或 2 处理）。

eg：删除下述树的15节点

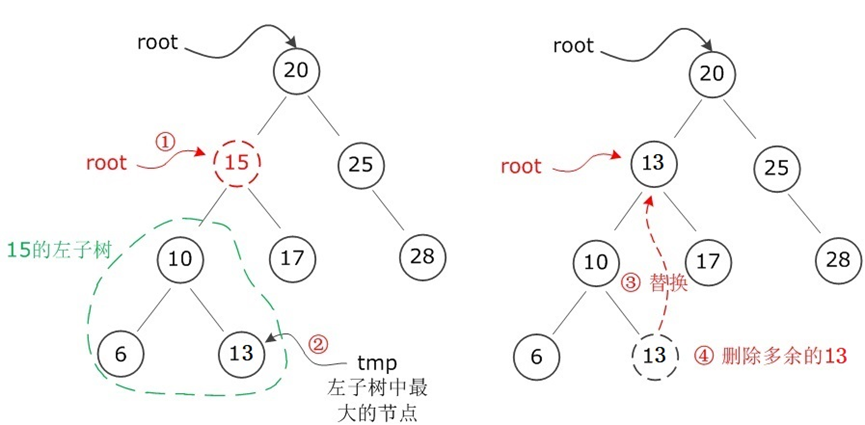
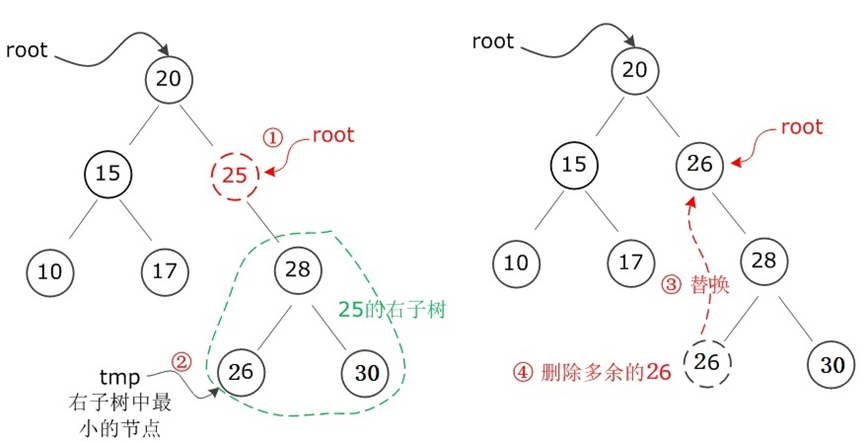
代码实现

// 找到左子树的最大节点（辅助函数）
BSTnode_t *BSTree_FindMax(BSTnode_t *root) {while (root->rchild != NULL) { // 最大节点在最右侧root = root->rchild;}return root;
}// BST删除节点
BSTnode_t *BSTree_Delete(BSTnode_t *root, DataType_t data) {if (root == NULL) { // 树空，无节点可删return NULL;}// 找到要删除的节点if (data < root->data) { // 删左子树的节点root->lchild = BSTree_Delete(root->lchild, data);} else if (data > root->data) { // 删右子树的节点root->rchild = BSTree_Delete(root->rchild, data);} else { // 找到目标节点，分3种情况删除// 情况1：叶子节点或只有一个子节点if (root->lchild == NULL) { // 无左子树，用右子树替换BSTnode_t *tmp = root->rchild;free(root); // 释放被删除节点return tmp;} else if (root->rchild == NULL) { // 无右子树，用左子树替换BSTnode_t *tmp = root->lchild;free(root);return tmp;}// 情况2：有两个子节点，找左子树最大节点替换BSTnode_t *maxLeft = BSTree_FindMax(root->lchild); // 左子树最大节点root->data = maxLeft->data; // 替换数据// 递归删除左子树的最大节点（此时maxLeft最多有一个子节点）root->lchild = BSTree_Delete(root->lchild, maxLeft->data);}return root;
}

BST 程序正确性验证

可借助drawtree.h工具生成可视化网页，步骤如下：
drawtree.h

• 将drawtree.h头文件与源文件放在同一目录，在源文件中用#include "drawtree.h"包含；
• 修改drawtree.h中的数据类型（如DataType_t）和节点结构体（确保与自定义的BSTnode_t一致，尤其是左 / 右指针名）；
• 在代码中调用drawtree()函数，传入 BST 的根节点；
• 编译并运行程序，当前目录会生成tree.html，打开网页即可查看 BST 的结构，验证插入 / 删除后的正确性。

二叉树经典算法题

算法 1：计算二叉树的总节点数

思路（递归）

• 空树：0 个节点；
• 非空树：1（根节点） + 左子树节点数 + 右子树节点数。

代码

int BSTree_GetTotalNodes(BSTnode_t *root) {if (root == NULL) {return 0;}return 1 + BSTree_GetTotalNodes(root->lchild) + BSTree_GetTotalNodes(root->rchild);
}

算法 2：计算二叉树的叶子节点数

思路（递归）

• 空树：0 个叶子；
• 若节点左、右子树均为空：1 个叶子；
• 否则：左子树叶子数 + 右子树叶子数。

代码

int BSTree_GetLeafNodes(BSTnode_t *root) {if (root == NULL) {return 0;}// 左右子树均空，是叶子节点if (root->lchild == NULL && root->rchild == NULL) {return 1;}// 递归统计左右子树的叶子return BSTree_GetLeafNodes(root->lchild) + BSTree_GetLeafNodes(root->rchild);
}

算法 3：计算二叉树的高度（深度）

思路（递归）

• 空树：高度 0；
• 非空树：1 + max (左子树高度，右子树高度)。

代码

int BSTree_GetHeight(BSTnode_t *root) {if (root == NULL) {return 0;}int leftH = BSTree_GetHeight(root->lchild);  // 左子树高度int rightH = BSTree_GetHeight(root->rchild); // 右子树高度return 1 + (leftH > rightH ? leftH : rightH); // 取较大值加1
}