图神经网络分享系列-transe(Translating Embeddings for Modeling Multi-relational Data) (一)
目录
一、摘要
二、介绍
三、基于翻译的模型
损坏三元组的构建
优化方法与约束
优化流程细节
四、相关工作
结构化嵌入(SE)模型特性
表达能力对比
性能表现分析
数学表达规范
图神经系列概览:图神经网络分享系列-概览-CSDN博客
一、摘要
我们探讨了在多关系数据中将实体及关系嵌入低维向量空间的问题,目标是提出一种易于训练、参数量较少且能扩展到超大规模数据库的规范模型。因此,提出TransE方法,该方法将关系建模为对实体低维嵌入的平移操作。尽管假设简单,但实验证明其有效性:TransE在两个知识库的链接预测任务中显著优于前沿方法。此外,该方法能成功训练包含100万实体、2.5万种关系和超1700万样本的大规模数据集。
二、介绍
多关系数据是指由实体节点和形式为(头实体,标签,尾实体)(记作(h, l, t))的边构成的有向图,每条边表示头实体与尾实体之间存在某种特定名称的关系。多关系数据模型在诸多领域具有关键作用,例如社交网络分析中实体代表成员、边代表好友/社交关系链;推荐系统中实体为用户和商品、边代表购买/评分/评论/搜索行为;又如Freebase、谷歌知识图谱或基因本体等知识库,其中实体表征抽象概念或现实世界中的具体对象,边则描述两者之间的语义关系。本研究聚焦于知识库(具体采用Wordnet和Freebase)的多关系数据建模,旨在通过自动化添加新事实来完善知识库,且无需额外先验知识。
多关系数据建模的核心在于提取实体间局部或全局的连接模式,预测时利用这些模式泛化特定实体与其他实体的观测关系。单关系中局部性可能仅依赖结构特征(如社交网络中"朋友的朋友是朋友"),也可能与实体特性相关(如"喜欢《星球大战4》的用户也可能喜欢《星球大战5》但对《泰坦尼克号》偏好不定")。相较于单关系数据可通过描述性分析后采用特定简单假设建模,多关系数据的难点在于局部性可能同时涉及不同类型的关系和实体,因此需要更通用的建模方法以协同考虑所有异构关系。
受协同过滤中用户/项目聚类或矩阵分解技术成功刻画单关系数据实体连接模式相似性的启发,现有多关系数据方法多在潜在属性关系学习框架下构建,即通过学习实体和关系的潜在表征(嵌入)进行操作。从随机块模型非参数贝叶斯扩展、张量分解模型到集体矩阵分解等早期多关系域扩展方法,近期研究更关注提升模型表达能力与普适性,包括贝叶斯聚类框架和基于能量的低维空间实体嵌入学习框架。然而模型表达力的增强伴随复杂度显著提升:模型假设难以解释、计算成本增高,且易因高容量模型正则化困难导致过拟合,或因非凸优化存在大量局部极值引发欠拟合。实际研究表明,线性模型在多种多关系数据集上性能接近最具表达力的双线性模型,这表明即便在复杂异构的多关系领域,恰当简洁的建模假设仍能实现精度与可扩展性的更优平衡。

三、基于翻译的模型
给定一个由三元组(h, l, t)构成的训练集 S,其中两个实体 h, t ∈ E(实体集合),关系 l ∈ L(关系集合),该模型学习实体和关系的向量嵌入。嵌入值位于 R^k 空间(k 为模型超参数),并用粗体字母表示相同符号。模型的核心思想是:由 l 标记的边所诱导的函数关系对应于嵌入的平移,即当(h, l, t)成立时,期望 h + l ≈ t(t 应是 h + l 的最近邻),否则 h + l 应远离 t。
在基于能量的框架下,三元组的能量等于 d(h + l, t),其中 d 为某种不相似性度量,通常采用 L1 或 L2 范数。为学习此类嵌入,需在训练集上最小化基于间隔的排序准则:
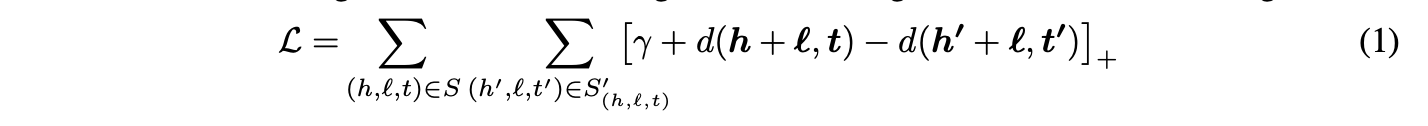
在数学表达式中,[x]⁺ 表示 x 的正部(即 max(0, x)),γ > 0 是一个边际超参数。
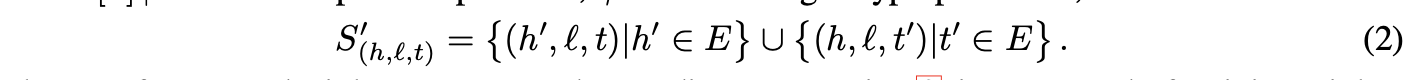
损坏三元组的构建
根据方程2构建的损坏三元组集合,由训练三元组中的头实体或尾实体(但不同时替换两者)被随机实体替换而成。损失函数(1)倾向于使训练三元组的能量值低于损坏三元组,因此自然实现了预期目标。需注意,对于同一实体,其嵌入向量在作为三元组头或尾时保持不变。
优化方法与约束
优化过程采用小批量随机梯度下降法,迭代更新可能的头实体h、关系l和尾实体t的嵌入。额外约束要求实体的嵌入向量L2范数为1(关系嵌入l无需正则化或范数约束)。该约束对模型至关重要(与先前嵌入方法[3, 6, 2]类似),可防止训练过程通过人为增大实体嵌入范数来 trivial 地最小化损失函数L。
优化流程细节
具体优化步骤如算法1所述:
- 实体和关系的嵌入均按文献[4]提出的随机方法初始化。
- 算法每轮主迭代中,先对实体嵌入向量归一化。
- 从训练集中采样小批量三元组作为当前训练批次。
- 对每个训练三元组,采样一个对应的损坏三元组。
- 以恒定学习率执行梯度步更新参数。
- 最终根据验证集性能终止算法。
四、相关工作
第一章节描述了关于知识库嵌入的大量研究工作。此处详细说明该模型与文献[3](结构化嵌入,Structured Embeddings或SE)及文献[14]中模型之间的关联性。
关键术语解析
- 知识库嵌入(KBs Embedding):将结构化知识转化为低维向量表示的技术。
- 结构化嵌入(SE):一种通过关系特定矩阵投影实体向量的经典嵌入方法。
结构化嵌入(SE)模型特性
SE [3] 将实体嵌入到 空间,关系则映射为两个矩阵
和
,其设计使得损坏三元组
的
值较大(正常三元组该值较小)。核心思想是:当两个实体属于同一三元组时,它们在依赖于特定关系的子空间中应具有相近的嵌入表示。为处理关系
可能存在的非对称性,模型对头实体和尾实体分别采用不同的投影矩阵。
表达能力对比
当差异函数采用 形式(例如
为范数函数),且嵌入维度为
时,SE 的表达能力严格优于当前模型(嵌入维度为
)。这是因为
维的线性算子可在
维子空间中重现仿射变换(通过约束所有嵌入的第
维为 1)。当
设为单位矩阵且
为平移变换时,SE 等价于 TransE 模型。
性能表现分析
尽管当前模型表达能力较弱,实验仍显示其性能优于 SE。原因可能包括:
- 该模型能更直接表征关系的真实特性
- 嵌入模型的优化本身具有挑战性
SE 的强表达能力反而可能导致欠拟合而非性能提升,第 4.3 节的训练误差数据支持了这一观点。
另一种相关方法是神经张量模型[14]。该模型的一个特例对应于学习三元组得分函数s(h, l, t)(被破坏的三元组得分较低),其形式为:
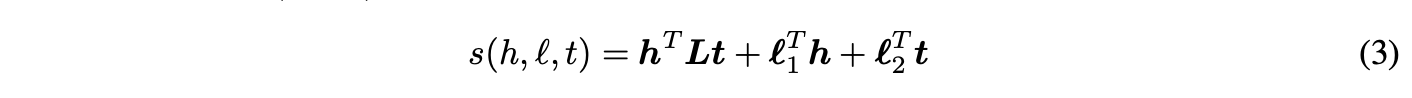
在数学表达式中,( )、(
) 和 (
) 均为依赖于参数 ( l ) 的矩阵或向量。若采用 TransE 模型并以平方欧氏距离作为相异性函数,可得以下关系:
关键术语说明
- (
): ( k \times k ) 维实矩阵
- (
): ( k ) 维实向量
- TransE: 一种知识图谱嵌入模型,通过平移操作建模实体关系
- 平方欧氏距离: 相异性度量函数,形式为 (
)
数学表达规范
若需进一步展开公式推导,可补充如下标准形式:
对于向量 ( \mathbf{h}, \mathbf{t} \in \mathbb{R}^k ) 和关系向量 ( \mathbf{r} \in \mathbb{R}^k ),TransE 的评分函数为: [ d(\mathbf{h} + \mathbf{r}, \mathbf{t}) = |\mathbf{h} + \mathbf{r} - \mathbf{t}|_2^2 ]
在范数约束(∥h∥₂=∥t∥₂=1)和排名准则(1)下,∥l∥₂在比较损坏三元组时不发挥作用。该模型通过评分函数hᵀt + lᵀ(t−h)对三元组进行评分,因此与文献[14]的模型(式(3))一致,其中L为单位矩阵,且l=l₁=−l₂。由于该模型与我们的研究同时发表,未能进行实验对比,但TransE的参数数量显著更少:这可以简化训练过程、防止欠拟合,并可能弥补其表达能力较弱的不足。
然而,TransE的简单形式(例如通过展开L2范数版本可视为编码一系列二元交互)存在局限性。对于需要建模h、l、t三者间三元依赖关系的数据,该模型可能失效。例如,在小规模Kinships数据集[7]上,TransE在交叉验证中的性能(通过精确率-召回率曲线下面积衡量)无法与前沿方法[11,6]竞争,因为此类三元交互在此场景中至关重要(参见文献[2]的讨论)。尽管如此,第4节的实验表明,对于处理Freebase等通用大规模知识库,应优先正确建模最常见的关系模式,正如TransE所做的那样。
关键术语说明
- 三元组(triplet):指知识图谱中头实体(h)、关系(l)、尾实体(t)组成的结构。
- 范数约束(norm constraints):限制向量模长为1,用于规范化嵌入表示。
- 交叉验证(cross-validation):评估模型泛化能力的统计方法。
- Freebase:大型开源知识库,常用于知识表示学习 benchmark。
本篇的内容就到这里结束了,相关实验放在下篇文章
传送门: