特征值与特征向量与SVD矩阵分解
特征值与特征向量
矩阵究竟做了什么?
矩阵对向量可以做拉伸也可以做旋转
[3001][xy]=[3xy]\left[\begin{array}{ll}3 & 0 \\ 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{l}3 x \\ y\end{array}\right][3001][xy]=[3xy]
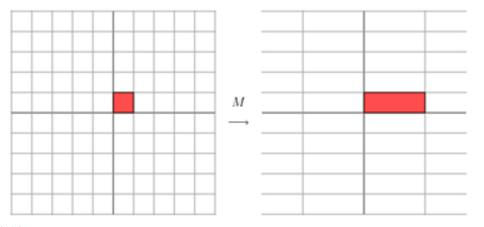
矩阵MMM定义为:
M=[1101]M=\left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]M=[1011]
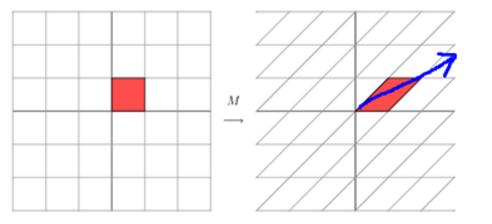
特征值和特征向量描述了什么?
拳击怎么赢?攻击的方向与力量!
我们可以把方向当做是特征向量,在这个方向上用了多大力量就是特征值。

数学定义
对于给定矩阵AAA,寻找一个常数λ\lambdaλ和非零向量xxx,使得向量xxx被矩阵AAA作用后所得的向量AxAxAx与原向量xxx平行,并且满足Ax=λxA x=\lambda xAx=λx
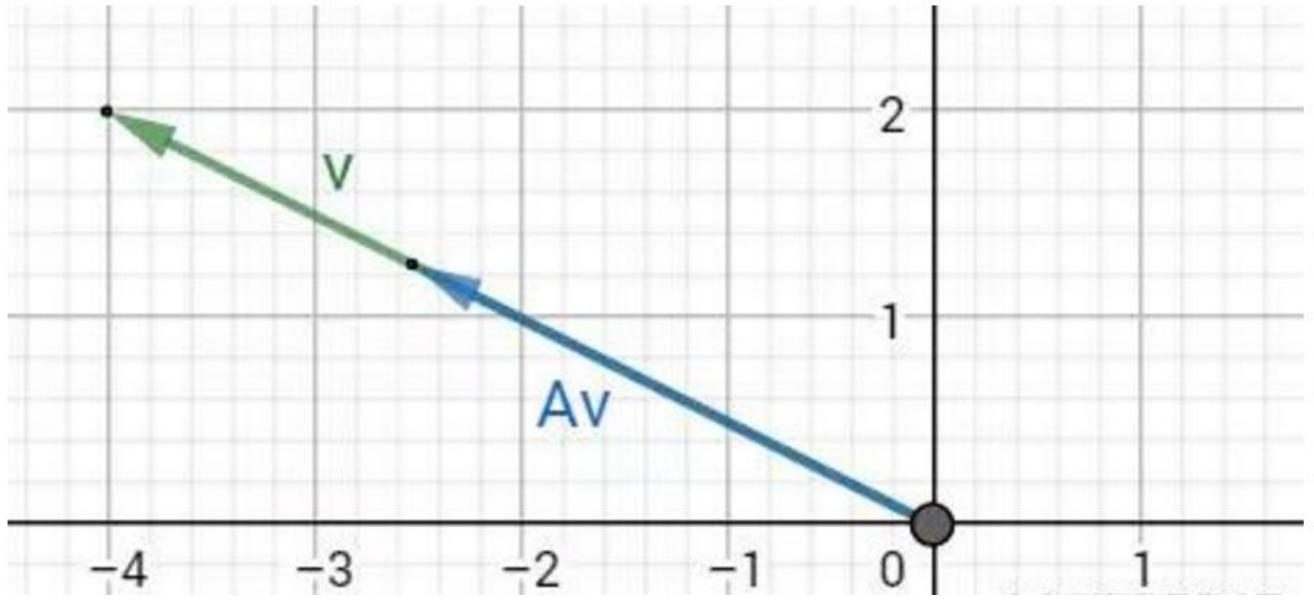
特征空间
特征空间中包含了所有的特征向量
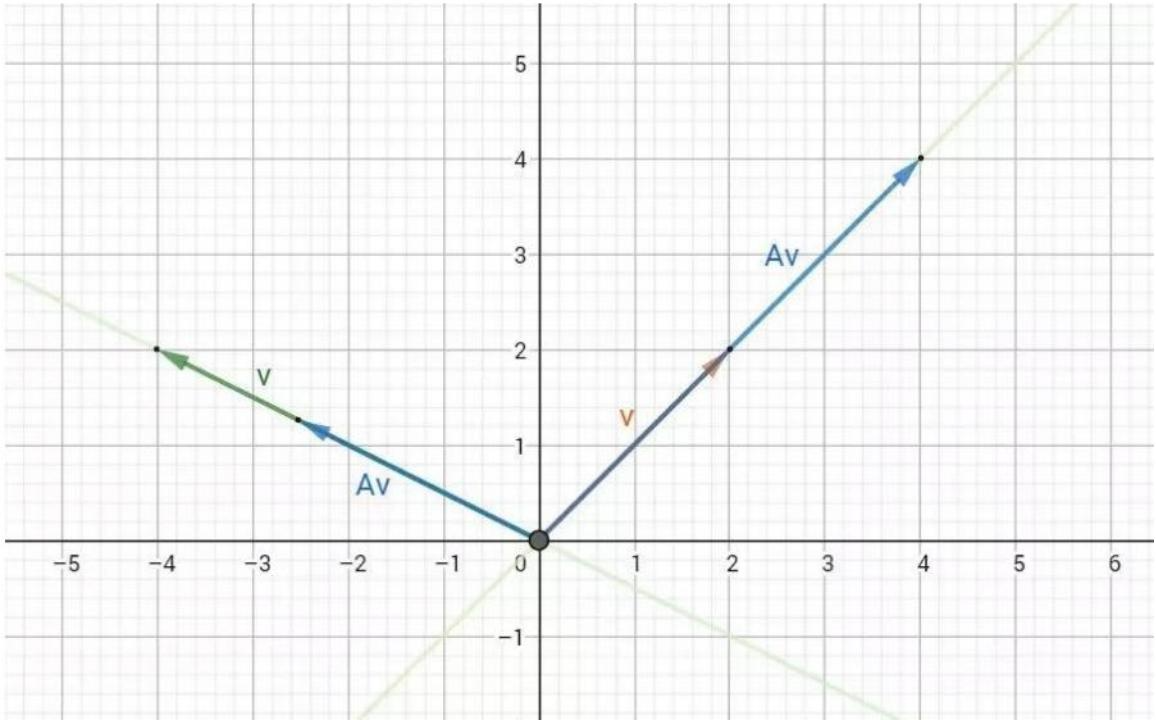
特征向量的应用
既然特征值表达了重要程度且和特征向量所对应,那么特征值大的就是主要信息了,基于这点我们可以提取各种有价值的信息了!

SVD矩阵分解
向量的表示及基变换
向量可以表示为(3,2)(3,2)(3,2)
实际上表示线性组合:x(1,0)⊤+y(0,1)⊤x(1,0)^{\top}+y(0,1)^{\top}x(1,0)⊤+y(0,1)⊤
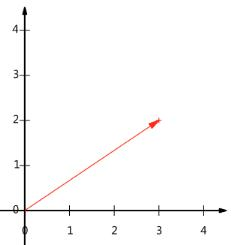
基:(1,0)(1,0)(1,0)和(0,1)(0,1)(0,1)叫做二维空间中的一组基
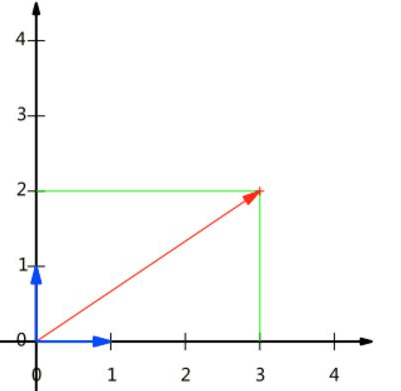
基变换(一)
基是正交的(即内积为0,或直观说相互垂直)
要求:线性无关
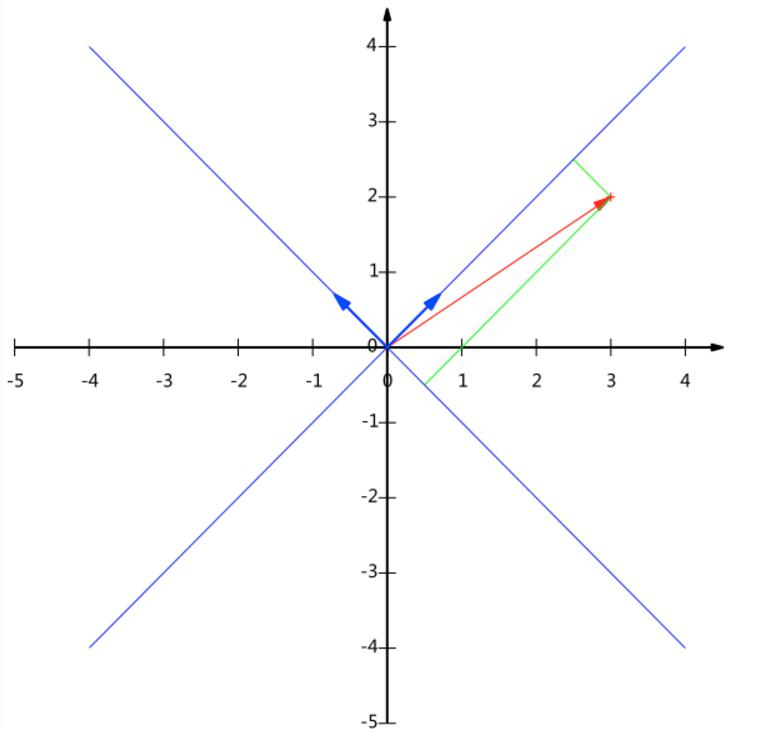
基变换(二)
变换:数据与一个基做内积运算,结果作为第一个新的坐标分量,然后与第二个基做内积运算,结果作为第二个新坐标的分量
数据(3,2)(3,2)(3,2)映射到基中坐标:
(1/21/2−1/21/2)(32)=(5/2−1/2)\left(\begin{array}{rr}1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2}\end{array}\right)\left(\begin{array}{l}3 \\ 2\end{array}\right)=\left(\begin{array}{r}5 / \sqrt{2} \\ -1 / \sqrt{2}\end{array}\right)(1/2−1/21/21/2)(32)=(5/2−1/2)
矩阵乘以一个向量
结果仍是一个向量
[3001][xy]=[3xy]\left[\begin{array}{ll}3 & 0 \\ 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{l}3 x \\ y\end{array}\right][3001][xy]=[3xy]
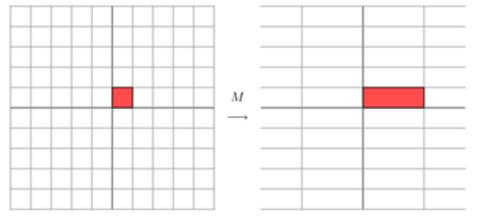
矩阵MMM定义为:
M=[1101]M=\left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]M=[1011]
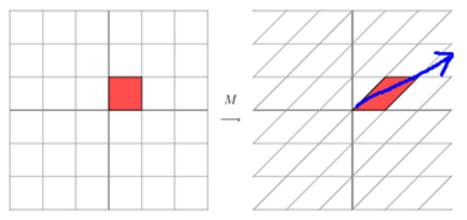
特征值分解
矩阵里面的信息有很多呀?来分一分吧!A=UΛU−1A=U \Lambda U^{-1}A=UΛU−1
当矩阵是N×NN \times NN×N的方阵且有NNN个线性无关的特征向量时就可以来玩啦!
这时候我们就可以在对角阵当中找比较大的啦,他们就是代表了!
SVD(一)
特征值分解不挺好的嘛,但是它被限制住了,如果我的矩阵形状变了呢?
但是问题也来了,如果MMM和NNN都很大呢?
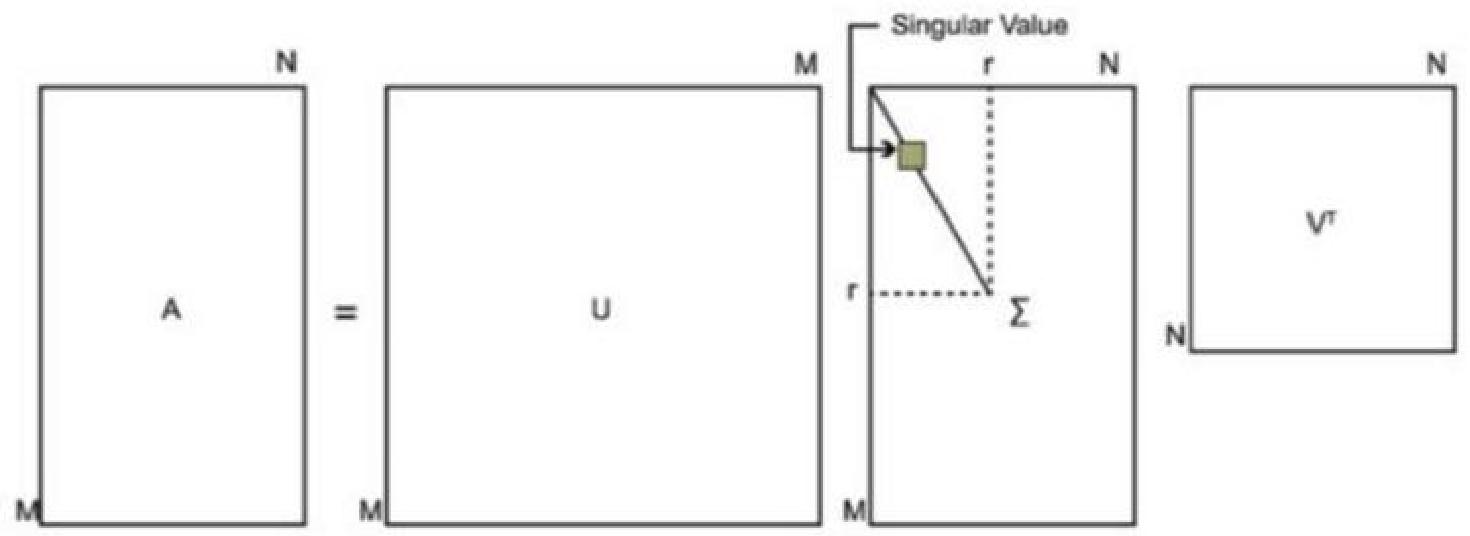
SVD(二)
照样按照特征值的大小来进行筛选,一般前10%的特征值(甚至更少)的和就占到了总体的99%了。
取前KKK个来看看吧!
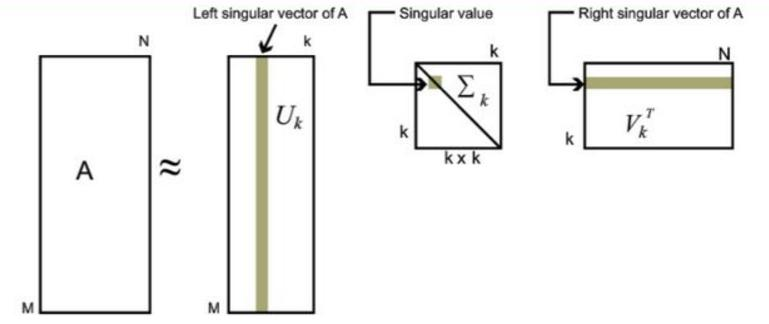
SVD推导(一)
前提:对于一个二维矩阵MMM可以找到一组标准正交基v1v_1v1和v2v_2v2使得Mv1Mv_1Mv1和Mv2Mv_2Mv2是正交的。
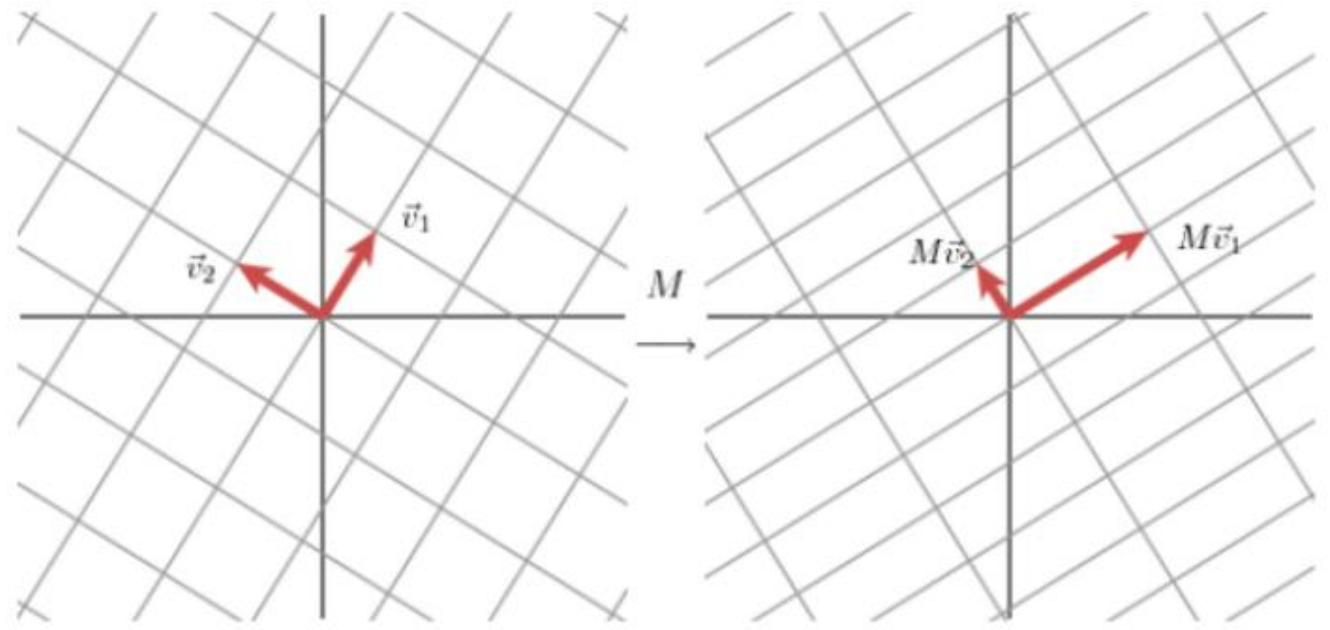
SVD推导(二)
使用另一组正交基u1u_1u1和u2u_2u2来表示Mv1Mv_1Mv1和Mv2Mv_2Mv2的方向
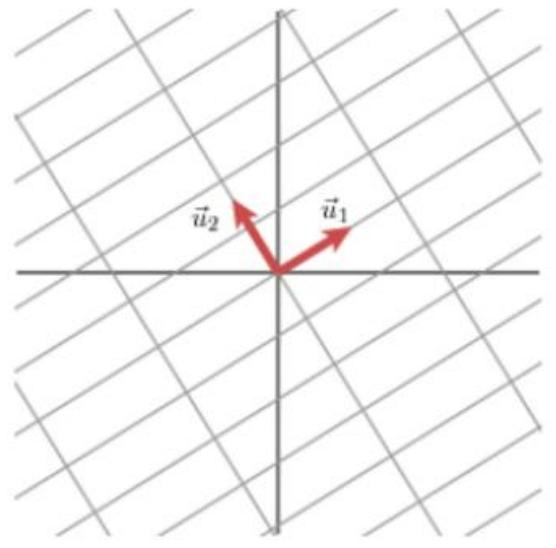
其长度分别为:∥Mv1∥=σ1\|Mv_1\| = \sigma_1∥Mv1∥=σ1,∥Mv2∥=σ2\|Mv_2\| = \sigma_2∥Mv2∥=σ2,可得:
Mv1=σ1u1Mv_1 = \sigma_1 u_1Mv1=σ1u1
Mv2=σ2u2Mv_2 = \sigma_2 u_2Mv2=σ2u2
对于向量XXX在这组基中的表示:x=(v1⋅x)v1+(v2⋅x)v2x = (v_1 \cdot x)v_1 + (v_2 \cdot x)v_2x=(v1⋅x)v1+(v2⋅x)v2
(点积表示投影的长度,可转换成行向量乘列向量 v⋅x=vTxv \cdot x = v^T xv⋅x=vTx)
可得:
Mx=(v1⋅x)Mv1+(v2⋅x)Mv2Mx = (v_1 \cdot x)Mv_1 + (v_2 \cdot x)Mv_2Mx=(v1⋅x)Mv1+(v2⋅x)Mv2
Mx=(v1⋅x)σ1u1+(v2⋅x)σ2u2Mx = (v_1 \cdot x)\sigma_1 u_1 + (v_2 \cdot x)\sigma_2 u_2Mx=(v1⋅x)σ1u1+(v2⋅x)σ2u2
从而:
Mx=u1σ1v1Tx+u2σ2v2TxMx = u_1 \sigma_1 v_1^T x + u_2 \sigma_2 v_2^T xMx=u1σ1v1Tx+u2σ2v2Tx
M=u1σ1v1T+u2σ2v2TM = u_1 \sigma_1 v_1^T + u_2 \sigma_2 v_2^TM=u1σ1v1T+u2σ2v2T
化简得:M=UΣVTM = U \Sigma V^TM=UΣVT
