使用BatchNorm偏置填充边界：确保推理一致性与数值稳定性

在深度学习模型中，BatchNorm（BN）层通过标准化数据来加速训练并提高模型的稳定性。然而，在实际应用中，边界区域的标准化常常存在一定的挑战，尤其是在推理阶段。偏置填充是一种有效的策略，它通过对边界数据进行平移，确保了边界区域的输出与中间区域的一致性。

本文将结合完整的推导公式和具体示例，深入探讨 为什么使用BN偏置填充边界，以及它如何确保推理阶段的稳定性和一致性。

---

1. BatchNorm 公式回顾

在讨论如何通过 偏置填充 来确保推理一致性之前，首先回顾一下 BatchNorm 层的标准化操作。BN 层的核心作用是将输入数据标准化，使其均值为 0，方差为 1，并通过偏置对数据进行平移调整。

BN 的标准化公式为：

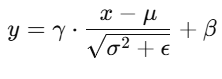
其中：

2. 为什么边界标准化不准确？

在推理图像的标准化过程中，BatchNorm 通常使用 全局均值和方差 来进行数据标准化，这对于图像的 中间区域 非常准确。然而，边界区域 由于缺少足够的邻域数据，它们的标准化通常依赖于全局统计量，而这些统计量无法准确反映边界区域的实际分布，从而导致标准化效果的失真。

具体来说，零填充 会改变图像的均值和方差：

• 均值 会由于填充的零而下降，因为填充的部分是零，对整体均值有影响。

• 方差 会增加，因为零的填充使得图像的分布范围扩大。

这导致图像的标准化效果 无法保持原有的均值为 0、方差为 1，特别是在 边界区域。因此，尽管 全局均值和方差 在推理时用于标准化，但它们对边界区域的 不适用性 会导致标准化失真，尤其是在图像被零填充时。

为什么偏移可以解决这个问题

偏置填充通过计算并填充 BN 层的偏置，有效地解决了这个问题。偏置的作用是 平移标准化后的数据，它能 弥补由于边界缺少足够的邻域数据 导致的标准化误差。通过 偏置填充，我们为 边界部分 提供了一个适当的修正，确保它们的标准化结果 与图像的其他区域一致，从而恢复了图像的标准化效果，并避免了推理阶段的标准化失真。

简而言之，偏移 通过对标准化结果进行 平移调整，有效补偿了边界部分因缺少邻域数据而导致的标准化误差，确保了图像在推理阶段的 稳定性和一致性。

具体例子：边界标准化不准确

假设我们有一个 5x5 的输入张量 x（例如，图像），其中值为：

步骤1：标准化（未填充边界）

对这个输入张量进行 BatchNorm 标准化。假设 batch 的均值 μ 和 方差 σ2 是基于整个图像计算的全局统计量，而不是每个小区域的统计量。对于标准化，我们使用以下公式：

假设我们计算出均值 μ=5.0 和方差 σ2=8.0 ，以及偏置 β=0 ，缩放系数 γ=1 ，那么标准化后的计算如下：

对于边界像素（例如 [0,0,0,0,0]），标准化将得到：

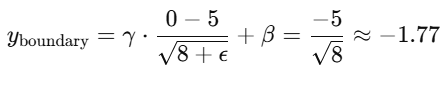
在这种情况下，边界像素的标准化结果会远离 0，这不是我们想要的，因为边界数据的标准化结果受到 均值 μ 和 方差 σ2 的影响，而 边界像素本身缺少足够的邻域数据来计算准确的均值和方差，导致它们的标准化结果 不如中间部分稳定。

步骤2：通过偏置填充来修正边界

现在，我们知道 BN 的偏置（β）实际上可以用来对标准化后的数据进行 平移，使得 边界部分的输出 与其他区域保持一致。假设 计算出来的偏置 是：

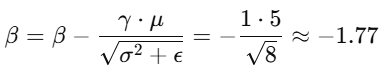
通过 填充偏置，我们实际上是用 计算出来的偏置值 来 调整边界部分的结果。在这种情况下，偏置填充后的边界部分会 恢复到与中间部分一致的输出。

步骤3：边界与中间区域的一致性

通过 偏置填充，边界部分的填充值将为 -1.77，而不是 0，确保推理时 边界数据与其他区域一致。通过这种方式，BN 层的偏置实际上确保了 边界区域的标准化补偿，使得推理阶段的 边界数据与其他区域的数据一致。

3. 偏置填充的代码实现

以下是两段关键代码的解释和实现：

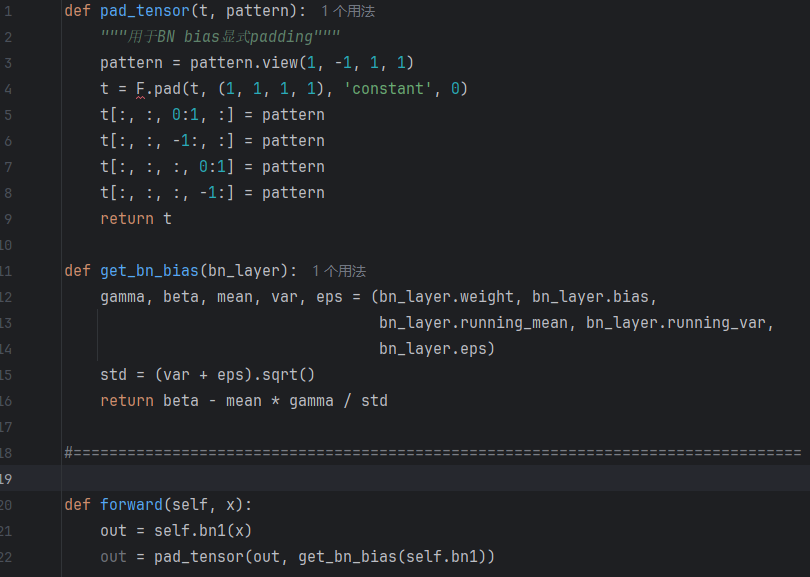
def pad_tensor(t, pattern):"""用于BN bias显式padding"""pattern = pattern.view(1, -1, 1, 1)t = F.pad(t, (1, 1, 1, 1), 'constant', 0)t[:, :, 0:1, :] = patternt[:, :, -1:, :] = patternt[:, :, :, 0:1] = patternt[:, :, :, -1:] = patternreturn t

这段代码的作用是将 BN 层的偏置 填充到输入张量的 四个边界（上、下、左、右），确保推理阶段边界部分的数据与其他区域一致。

def get_bn_bias(bn_layer):gamma, beta, mean, var, eps = (bn_layer.weight, bn_layer.bias,bn_layer.running_mean, bn_layer.running_var,bn_layer.eps)std = (var + eps).sqrt()return beta - mean * gamma / std

此函数用于 提取 BN 层的偏置，计算 β - (γ * μ / std)，即 标准化后的平移值，该值用于在 pad_tensor 函数中填充边界部分。

y = bn(x)  # 先对内部区域做BN
y_padded = pad_tensor(y, get_bn_bias(bn))

在这种方式中，首先对输入进行 BN 变换，然后使用计算得到的偏置填充边界部分。