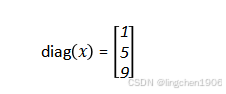衡水需要做网站的公司wordpress的模板文件下载

3.1 元素输入法

元素输入法是最简单，也是最常用的一种矩阵的生成方法。例如：

注意：

1. 整个矩阵必须用“[]”括起来；
2. 元素之间必须用逗号“，”或空格分开；
3. 矩阵的行与行之间必须用“；”或者回车键“Enter”隔开；
4. 元素按照先列后行的方式进行存储。

3.2 设定步长生成法

设定步长生成法用于生成一维行数组。

格式：x=a：inc：b

其中a是数组的第一个元素；inc是相邻两个元素之间的间隔；b是数组的最后一个元素。

例如：x=1：3：25

说明：

（1）若b-a是inc的整数倍，则最后一个元素是b；否则小于b。

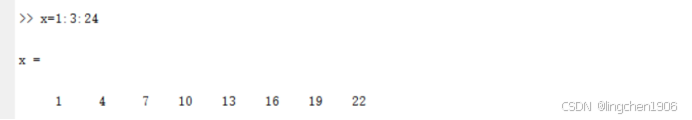
（2）若inc=1，可简写为x=a：b。

（3）inc可以取整数，也可以取复数。

遇到的警告 "Colon operands must be real scalars" 是因为在 MATLAB 中使用冒号运算符 : 时，中间的步长值使用了复数 3i。

冒号运算符的正确语法是 start:step:end，其中 start、step 和 end 都必须是实数标量，而不能是复数。

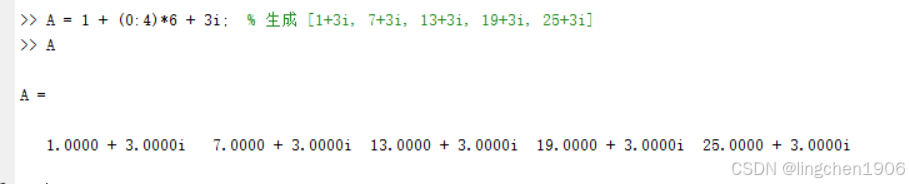
在例子中，虽然写了 1:3i+6:25，但 MATLAB 实际上忽略了复数部分的虚部，只使用了实部进行计算：

• 起始值：1
• 步长值：6（因为 3i 的实部是 0，0+6=6）
• 结束值：25

所以最终结果 A = [1 7 13 19 25] 实际上是按照 1:6:25 计算得到的，这就是为什么虽然有警告但仍然得到了结果。

如果你确实需要生成包含复数的数组，可以使用其他方法，例如：

3.3 均匀采样生成法

均匀采样生成法用于生成一维行数组。

格式：x=linspace（a，b，n）

其中，a，b分别为生成数组的第一个和最后一个元素；n为采样总点数。

例如：x=linspace（1，25，3）

从定义可以看出，该指令的作用与x=a：（b-a）/（n-1）：b相同。

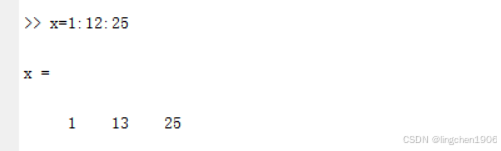
3.4 几种特殊矩阵的创建

特殊矩阵的创建命令如下表：

命令	说明
[]	空矩阵
zeros	全零矩阵
ones	全一矩阵
eye	单位矩阵
magic	魔方矩阵
rand	均匀随机矩阵
randn	高斯随机矩阵
diag	对角矩阵

（1）空矩阵

A=[]  %用于删除某个元素或者矩阵。

例：把矩阵A的第一个元素删除。

如下：

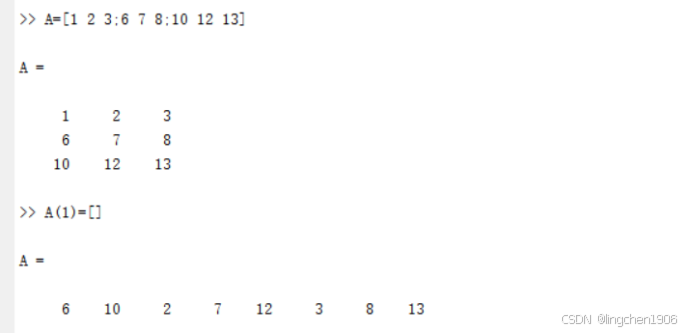
（2）全零矩阵

A=zeros（2，3）  %生成元素全为零的2×3阶矩阵。

（3）全一矩阵

A=ones（2，3）   %生成元素全为1的2×3阶矩阵。

（4）单位矩阵

A=eye（3，4） %使用eye（m，n）可得到一个允许的最大单位矩阵，其他位置补零。

（5）魔方矩阵

X=magic（3）  %用于产生一个3×3阶的魔方矩阵。

魔方矩阵（Magic Square）是一种特殊的n 阶方阵，其核心特征是每行、每列以及两条主对角线的元素之和都相等，这个相等的和被称为 “魔数”（Magic Constant）。

魔方矩阵在数学、数论、组合数学以及趣味数学中都有重要地位，且具有深厚的历史背景，古代文明（如中国、印度、阿拉伯等）都曾研究过这类矩阵。

魔方矩阵的核心性质

1. 阶数定义：通常以 “n 阶” 表示，指矩阵的行数和列数均为 n（n≥1，且多为正整数）。
2. 魔数计算：对于 n 阶魔方矩阵（元素为 1 到 n² 的连续整数，即 “标准魔方矩阵”），其魔数固定为：
   魔数 = n×(n² + 1)÷2
   例如：
   • 3 阶魔方矩阵的魔数为 3×(9 + 1)÷2 = 15；
   • 4 阶魔方矩阵的魔数为 4×(16 + 1)÷2 = 34。
3. 元素特点：标准魔方矩阵的元素是 1 到 n² 的连续整数，且每个数只出现一次（即 “幻方” 的经典定义）；非标准魔方矩阵可以使用其他数字，但需满足行、列、对角线和相等的条件。

常见阶数的魔方矩阵示例

3 阶魔方矩阵（最经典）

3 阶魔方矩阵是最小的奇数阶非平凡魔方矩阵，其元素为 1-9，每行、每列、对角线之和均为 15：

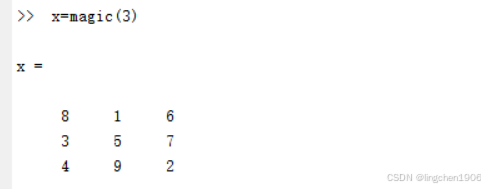
• 行：8+1+6=15，3+5+7=15，4+9+2=15；
• 列：8+3+4=15，1+5+9=15，6+7+2=15；
• 对角线：8+5+2=15，6+5+4=15。

4 阶魔方矩阵（偶数阶）

4 阶魔方矩阵元素为 1-16，魔数为 34，例如：

魔方矩阵的分类

根据阶数的奇偶性，魔方矩阵可分为两类：

奇数阶魔方矩阵（n 为奇数）：

可通过 “Siamese 方法”（斜步法）构造，核心是从矩阵底部中间位置开始，按特定方向（通常是右上）依次填入数字，遇到边界或已填元素时调整位置。

偶数阶魔方矩阵：

当 n 为4 的倍数（如 4、8 阶）：可通过 “对称交换法” 构造，将矩阵分为 4×4 子块，交换特定位置的元素。

当 n 为2 的倍数但不是 4 的倍数（如 6、10 阶）：构造更复杂，需结合奇数阶的构造方法分段处理（称为 “单偶数阶”）。

魔方矩阵的应用与意义

• 数学研究：作为组合数学的经典问题，其构造方法涉及数论和对称性分析。
• 历史文化：古代被视为神秘符号，如中国的 “洛书”（3 阶魔方矩阵）被认为是最早的魔方矩阵之一，记载于《周易》等典籍中。
• 计算机科学：常用于算法设计（如矩阵填充、回溯法练习）和密码学中的随机数生成参考。

（6）随机矩阵

1. rand（）均匀随机矩阵用于生成（0，1）区间上均匀分布的随机变量，其基本语法如下：

rand（[M，N，P，...] ）

例：

A=rand（2，4） %生成随机的2×4阶矩阵

生成排列成M×N×P...多维向量的随机数。如果只写M，则生成M×M阶矩阵；如果参数为[M,N],则可以省略到方括号。

2. randn（）高斯随机矩阵用于生成服从标准正态分布（均值为0，方差为1）的随机数，其基本语法和rand（）类似：

randn（[M,N,P...]）

生成排列成M×N×P...多维向量的随机数。如果只写M，则生成M×M阶矩阵；如果参数为[M,N],可以省略掉方括号。

3. rand() 与 randn() 的核心对比

维度	rand()	randn()
分布类型	(0, 1) 区间均匀分布	标准正态分布（均值 0，方差 1）
语法共性	维度参数规则、括号省略逻辑完全一致	维度参数规则、括号省略逻辑完全一致
应用场景差异	需“无偏向随机数”场景（如等概率模拟、均匀初始化）	需“自然波动规律”场景（如噪声模拟、正态分布物理量建模）

4. 理解“生成排列成多维向量的随机数”，需结合 Matlab 中数组的维度特性、函数参数规则来拆解，核心逻辑如下：

1. “多维向量”实为 多维数组

在 Matlab 语境中，此处“向量”是广义的数组概念（突破数学中“一维向量”的狭义定义）。Matlab 支持创建任意维度的数组（如二维矩阵、三维“行-列-页”结构、四维及以上张量），因此“多维向量”本质是多维数组。

2. M，N，P...的作用：定义各维度的长度

rand()/randn() 的参数 是维度尺寸参数，每个字母对应一个维度的“长度”：

• 第 1 个参数  → 数组第 1 维的长度（如“行数”）；
• 第 2 个参数  → 数组第 2 维的长度（如“列数”）；
• 第 3 个参数  → 数组第 3 维的长度（如“页数/层数”）；
• 更多参数 → 对应更高维度的长度。

3. “排列成M×N×P... ”：按维度参数构造数组结构

函数会先根据M，N，P...的数量和数值，确定数组的维度数量和各维度大小，再在这个预定义结构中填充随机数。结合场景具象化理解：

（1）二维数组（矩阵）场景

若输入 2 个参数 M，N（如 rand(2, 4)）：

• 维度数量：2 维（行、列）；
• 各维长度：第 1 维（行）长度 = M=2，第 2 维（列）长度 = N=4；
• 结果：生成 2 行 4 列的二维数组（矩阵），每个元素是 rand() 生成的 (0,1) 均匀随机数，或 randn() 生成的标准正态分布数。

（2）三维数组场景

若输入 3 个参数M，N，P（如 rand(2, 3, 2)）：

• 维度数量：3 维（行、列、页）；
• 各维长度：第 1 维（行）=M=1 ，第 2 维（列）=N=3 ，第 3 维（页）=P=2 ；
• 结果：生成 “2 行 × 3 列 × 2 页” 的三维数组。可想象为“2 个独立的 2 行 3 列矩阵叠在一起”，每个位置填充随机数。

（3）更高维数组场景

若输入 4 个参数M，N，P，Q（如 rand(1, 2, 3, 4)）：

• 维度数量：4 维；
• 各维长度：第 1 维 = M=1，第 2 维 =N=2 ，第 3 维 = P=3，第 4 维 = Q=4；
• 结果：生成 1×2×3×4 的四维数组，结构由 4 个维度长度共同定义，每个元素位置填充随机数。

5. 在 Matlab 中，“扩展数组到更高维度”可通过生成新的高维数组或改造已有数组维度实现。结合rand()/randn() 的语法逻辑，以下是详细方法拆解：

对已有数组扩展维度（非随机数组的维度改造）

若要对已存在的非随机数组（如数值矩阵、向量）扩展维度，可通过以下通用方法：

1. 使用 cat() 函数“沿维度拼接”

cat(DIM, A, B, ...) 可沿指定维度 DIM 拼接多个数组，实现维度扩展。

示例：将两个 2×3 矩阵沿第 3 维拼接，得到 2×3×2 三维数组：

A = ones(2, 3);  % 2×3 全1矩阵

B = zeros(2, 3); % 2×3 全0矩阵

C = cat(3, A, B);% 沿第3维拼接，生成 2×3×2 三维数组

2. 使用 reshape() 函数“重塑维度”

reshape(A, M, N, P, ...) 可将数组 A 重塑为指定维度的新数组（要求元素总数匹配）。

示例：将 1×6 行向量重塑为 2×3 矩阵（二维），或 1×2×3 三维数组：

V = 1:6;                  % 1×6 行向量（元素总数6）

M2 = reshape(V, 2, 3);    % 重塑为 2×3 矩阵（2×3=6，元素总数匹配）

M3 = reshape(V, 1, 2, 3); % 重塑为 1×2×3 三维数组（1×2×3=6，元素总数匹配）

3. 直接赋值“扩展维度”

对数组的新维度位置直接赋值，Matlab 会自动扩展维度并填充默认值（如 NaN 或 0，依场景而定）。

示例：将 2×3 矩阵扩展为 2×3×2 三维数组：

A = ones(2, 3);  % 2×3 矩阵

A(:, :, 2) = 2;  % 给第3维的第2层赋值，自动扩展维度为 2×3×2

4. 扩展数组维度的核心路径

场景	核心方法	示例（代码片段）
生成随机高维数组	用 rand()/randn() 的多维度参数 [M, N, P, …] 定义维度大小	rand(2, 3, 2) 生成 2×3×2 均匀随机三维数组
扩展已有数组维度	① cat() 沿指定维度拼接；② reshape() 重塑维度；③ 直接赋值新维度位置	cat(3, A, B) 沿第3维拼接数组；reshape(V, 1, 2, 3) 重塑维度

通过上述方法，可以灵活地在 Matlab 中创建或改造数组维度，覆盖从二维矩阵到高维张量的多样化需求。

（7）对角矩阵

（1）diag（x），当输入x为向量的时候，输出结果为对角矩阵。

当输入x是一个向量（可以是行向量或列向量）时，diag(x)的输出是一个对角矩阵：

• 矩阵的主对角线（从左上角到右下角的对角线）元素为向量x的各个分量；
• 矩阵的其他位置元素均为0；
• 矩阵的阶数（行数和列数）等于向量x的长度。

示例：

若x = [a, b, c]（长度为3的行向量），则：

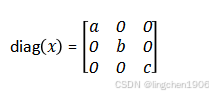
具体数值例子：设x = [1, 2, 3]，则：

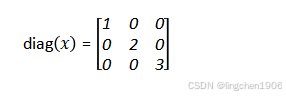
（2）diag（x，k），形成以x作为第k条对角线元素，其他位置为0的矩阵。

当输入x是向量，且额外指定参数k时，diag(x, k)的输出是一个非主对角线矩阵：

1. 矩阵的第k条对角线元素为向量x的各个分量；
2. 其他位置元素均为0；
3. k的含义：k=0表示主对角线，k>0表示主对角线上方第k条对角线，k<0表示主对角线下方第|k|条对角线；
4. 矩阵的阶数：若x长度为n，则矩阵阶数为n + |k|（确保x的所有元素能放在第k条对角线上）。

示例：

设x = [1, 2]（长度为2），k=1（主对角线上方第1条对角线），则矩阵阶数为2 + 1 = 3，输出为：

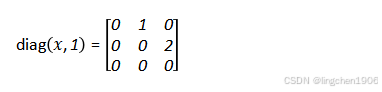
• 若k=-1（主对角线下方第1条对角线），输出为：

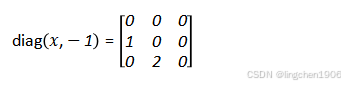
（3）当输入x为矩阵的时候，输出结果为提取该矩阵对角线元素形成的列向量。

当输入x是一个矩阵时，diag(x)的输出是一个列向量：

向量的元素为矩阵x的主对角线元素（从左上角到右下角依次提取）；

向量长度等于矩阵x的阶数（若x是n×n矩阵，则向量长度为n）。

示例：

设x是3×3矩阵：

其主对角线元素为1, 5, 9，则：